Разрабатываемая в данном разделе теория многомерно-матричного дифференцирования базируется на определении многомерной матрицы (2.1.1).
Определение многомерно-матричной производной
Прежде всего дадим определение многомерно-матричной производной [46]. Пусть 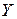 –
–  -мерная гиперпрямоугольная матрица
-мерная гиперпрямоугольная матрица
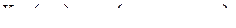 (3.2.1)
(3.2.1)
зависящая некоторым образом от  -мерной гиперпрямоугольная матрицы
-мерной гиперпрямоугольная матрицы  ,
,
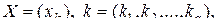 (3.2.2)
(3.2.2)
где 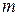 и
и  – мультииндексы. Производной матрицы
– мультииндексы. Производной матрицы 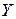 по матрице
по матрице  назовем
назовем 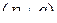 -мерную матрицу
-мерную матрицу 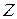 , определяемую выражением
, определяемую выражением
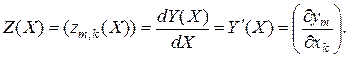 (3.2.3)
(3.2.3)
Из определения (3.2.3) видно, что элемент 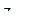 матрицы
матрицы 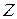 определяется как частная производная
определяется как частная производная
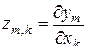 ,
,
и в матрице 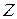 индексы матрицы
индексы матрицы  следуют за индексами матрацы
следуют за индексами матрацы 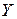 (соблюдается естественный порядок следования индексов). В отличие от работы [40] здесь индексы матриц
(соблюдается естественный порядок следования индексов). В отличие от работы [40] здесь индексы матриц  и
и 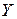 не делятся на строчные и столбцовые, и не нарушается естественный порядок следования индексов в производной.
не делятся на строчные и столбцовые, и не нарушается естественный порядок следования индексов в производной.
Производные высших порядков определяются последовательным дифференцированием:
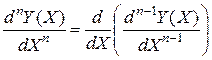 ,
,
или
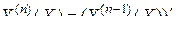 .
.
Известную скалярно-матричную производную (3.1.2) получаем как частный случай многомерно-матричной производной (3.2.3) при  ,
,  .
.
Докажем основные правила многомерно-матричного дифференцирования.
Производная сложной функции
Пусть  – многомерно-матричная функция (
– многомерно-матричная функция ( 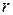 -мерная матрица)
-мерная матрица)
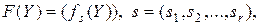
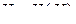 –
– 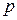 -мерная матрица,
-мерная матрица,

 –
–  -мерная матрица с различными (несовпадающими) элементами,
-мерная матрица с различными (несовпадающими) элементами,
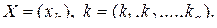
Тогда производная 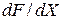 определяется как следующее
определяется как следующее 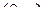 -свернутое произведение:
-свернутое произведение:
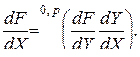 (3.2.4)
(3.2.4)
Докажем формулу (3.2.4). По определению (3.2.3) производная 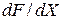 является
является 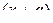 -мерной матрицей
-мерной матрицей
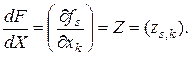
Так как для каждого элемента этой матрицы имеем формулу [30]
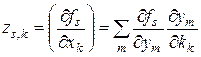 ,
,
то это означает справедливость формулы (3.2.4).
Более общим является случай функции 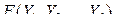 , где
, где 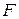 –
– 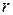 -мерная матрица,
-мерная матрица, 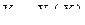 –
–  -мерные матрицы,
-мерные матрицы, 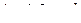 ,
,  –
–  -мерная матрица. Тогда
-мерная матрица. Тогда
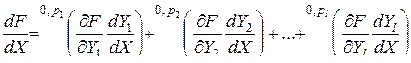 . (3.2.5)
. (3.2.5)
Эта формула следует из того, что для каждого элемента 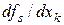 справедливо равенство [30]
справедливо равенство [30]
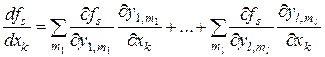 .
.
Если дифференцируемая сложная функция  ,
, 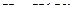 , явно зависит от аргумента
, явно зависит от аргумента  , т. е. имеет вид
, т. е. имеет вид  , то
, то
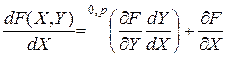 .
.
Эта формула вытекает из существующей для этого случая формулы дифференцирования для отдельного элемента матрицы 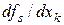 [30]
[30]
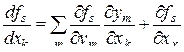 .
.
Производная произведения
Пусть 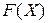 –
–  -мерная матрица,
-мерная матрица,
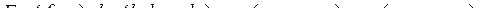
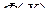 –
– 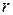 -мерная матрица,
-мерная матрица,
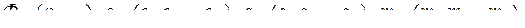
 –
–  -мерная матрица,
-мерная матрица,
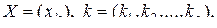
причем 
 ,
,  Справедлива следующая формула дифференцирования
Справедлива следующая формула дифференцирования  -свернутого произведения матриц
-свернутого произведения матриц 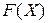 и
и 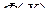 :
:
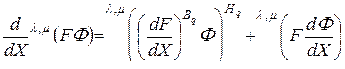 . (3.2.6)
. (3.2.6)
Здесь символами 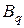 и
и 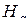 обозначены подстановки типа «вперед» и «назад» (2.8.11), (2.8.12) соответственно. Количество индексов подстановок
обозначены подстановки типа «вперед» и «назад» (2.8.11), (2.8.12) соответственно. Количество индексов подстановок 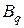 и
и 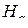 равно размерности транспонируемых матриц.
равно размерности транспонируемых матриц.
Для доказательства формулы (3.2.6) введем обозначения
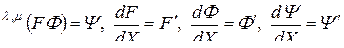 .
.
По определению 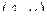 -свернутого произведения (2.2.17) для матриц
-свернутого произведения (2.2.17) для матриц 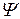 и
и  будем иметь выражения
будем иметь выражения
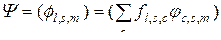 ,
,
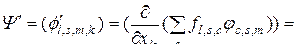
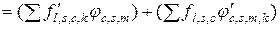 . (3.2.7)
. (3.2.7)
Второе слагаемое в правой части выражения (3.2.7) дает второе слагаемое в формуле (3.2.6), т.е.
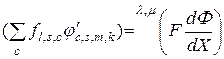 . (3.2.8)
. (3.2.8)
Первое слагаемое в правой части выражения (3.2.7) есть 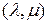 -свернутое произведение матриц
-свернутое произведение матриц 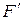 и
и 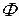 , однако свертывание производится не по внутренним индексам, как это принято в определении (2.2.17). Обозначим такое произведение как
, однако свертывание производится не по внутренним индексам, как это принято в определении (2.2.17). Обозначим такое произведение как 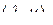 -свернутое,
-свернутое,
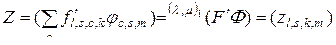 .
.
Выразим 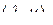 -свернутое произведение через
-свернутое произведение через 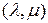 -свернутое произведение со свертыванием по внутренним индексам. Для этого введем матрицу
-свернутое произведение со свертыванием по внутренним индексам. Для этого введем матрицу
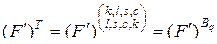 , (3.2.9)
, (3.2.9)
где символом 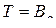 обозначена подстановка типа «вперед». Из формулы (3.2.9) следует, что
обозначена подстановка типа «вперед». Из формулы (3.2.9) следует, что
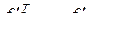 . (3.2.10)
. (3.2.10)
Найдем 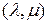 -свернутое произведение матриц
-свернутое произведение матриц 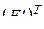 и
и 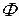
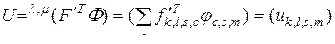 . (3.2.11)
. (3.2.11)
Подставив в формулу (3.2.11) выражение (3.2.10), получим
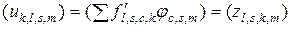 .
.
Из последнего равенства видно, что матрицы 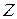 и
и 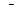 связаны соотношениями транспонирования
связаны соотношениями транспонирования
 ,
, 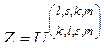 . (3.2.12)
. (3.2.12)
В результате первое слагаемое в выражении (3.2.7) приведено к виду
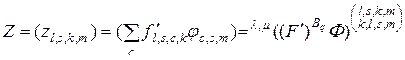 . (3.2.13)
. (3.2.13)
Однако порядок следования индексов в матрице (3.2.13) отличается от порядка следования индексов в производной  (3.2.7). Поэтому от матрицы Z необходимо перейти к матрице
(3.2.7). Поэтому от матрицы Z необходимо перейти к матрице 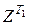 так, чтобы выполнялось условие
так, чтобы выполнялось условие
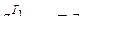 . (3.2.14)
. (3.2.14)
Подставляя выражение (3.2.12) в равенство (3.2.14), получаем
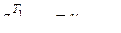 ,
,
или
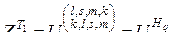 , (3.2.15)
, (3.2.15)
Учитывая формулу (3.2.11), запишем матрицу (3.2.15) в виде
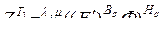 . (3.2.16)
. (3.2.16)
Теперь первое слагаемое в выражении (3.2.7) записано в форме (3.2.16), а второе слагаемое – в форме (3.2.8), что и доказывает формулу (3.2.6).
Производная неявной функции
Пусть функция 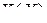 задана неявно равенством
задана неявно равенством
 , (3.2.17)
, (3.2.17)
где 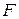 –
– 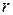 -мерная матрица,
-мерная матрица,
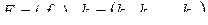 ,
,
 –
–  -мерная матрица,
-мерная матрица,
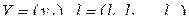 ,
,
 –
–  -мерная матрица,
-мерная матрица,
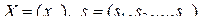 .
.
Тогда производная 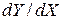 есть
есть 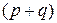 -мерная матрица, которая находится как решение следующего многомерно-матричного уравнения
-мерная матрица, которая находится как решение следующего многомерно-матричного уравнения
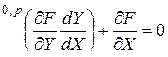 . (3.2.18)
. (3.2.18)
Действительно, расписав равенство (3.2.17) поэлементно,
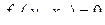 ,
, 

находим, что производные 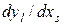 могут быть получены из системы линейных алгебраических уравнений [30]
могут быть получены из системы линейных алгебраических уравнений [30]
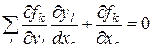 . (3.2.19)
. (3.2.19)
Система уравнений (3.2.19) в многомерно-матричной форме имеет вид (3.2.18).
Если функция 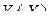 задана соотношением
задана соотношением
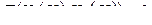 , (3.2.20)
, (3.2.20)
где 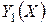 –
–  -мерная матрица,
-мерная матрица, 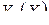 –
– 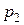 -мерная матрица,
-мерная матрица,  –
–  -мерная матрица, то
-мерная матрица, то  определяется как решение уравнения
определяется как решение уравнения
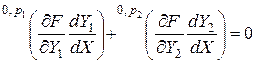 . (3.2.21)
. (3.2.21)
Это следует из правила (3.2.5).
Дата: 2019-02-02, просмотров: 805.