Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Очень часто приходится транспонировать 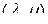-свернутое произведение многомерных матриц. В теории обычных матриц при транспонировании произведения множители транспонируются и меняются местами. Для многомерных матриц аналогичное правило имеет место лишь при транспонировании 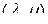- свернутого произведения соответственно некоторой подстановке специального вида. Это правило было получено Соколовым Н. П. [81], однако представляется недостаточно формализованным. С использованием введенных в разделе 2.8 подстановок ему можно придать строго формализованный вид, а также получить некоторые другие правила транспонирования [51]. Для наглядности полученных формул транспонирования структуру матрицы будем выделять указанием количества кэлиевых, скоттовых и свободных индексов.

Теорема 2.4 (о транспонировании 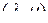-свернутого произведения соответственно подстановке специального вида). Пусть

 –

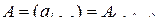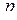-мерная матрица и

 –

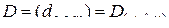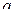- мерная матрица, причем

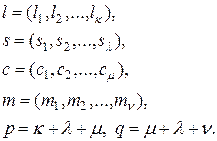
Тогда справедливо равенство

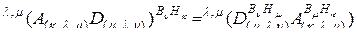,                 (2.10.1)

Докажем равенство (2.10.1). Для этого обозначим

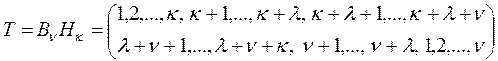, (2.10.2)

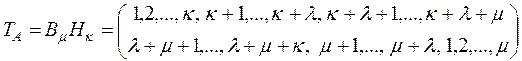, (2.10.3)

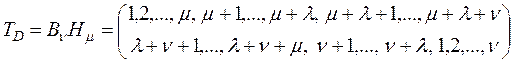. (2.10.4)

Здесь подстановки записаны в рангах. Тогда формула транспонирования (2.10.1) примет вид

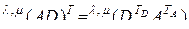.                                    (2.10.5)

Найдем левую часть равенства (2.10.5). Найдем сначала ,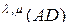

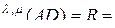
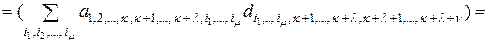
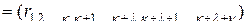.                          (2.10.6)

Транспонируем теперь 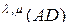 в соответствии с подстановкой  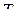(2.10.2).

.

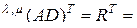
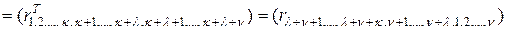Раскрывая здесь матрицу 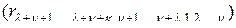 по формуле (2.10.6), для левой части равенства (2.10.5) будем иметь

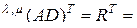
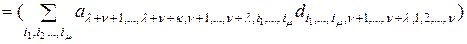.   (2.10.7)

Для правой части доказываемого равенства (2.10.5) получим

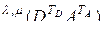
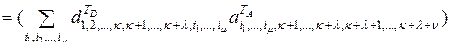. (2.10.8)

Заменяя здесь элементы матриц 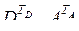 в соответствии с формулой транспонирования (2.8.3) и подстановками  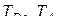(2.10.3), (2.10.4), будем иметь

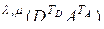
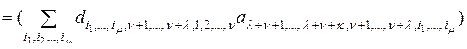. (2.10.9)

Мы видим, что правые части выражений (2.10.7) и (2.10.9) равны. Следовательно, равны и левые части этих выражений. Теорема доказана.

Приведем частные случаи формулы (2.10.1). При получаем

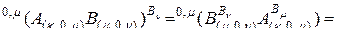
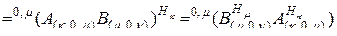.               (2.10.10)

В случаях 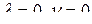, или 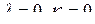, т. е. когда одна из матриц полностью сворачивается, получим

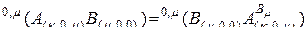
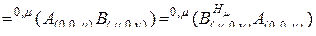.               (2.10.11)

Если 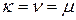, т. е. матрицы  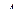и 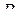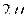-мерные, получим

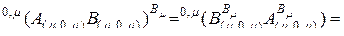
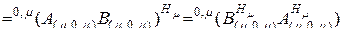.            (2.10.12)

При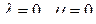

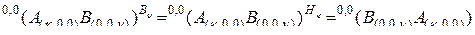. (2.10.13)

Есл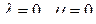и  и 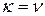, т. е. обе матрицы 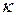-мерные, то

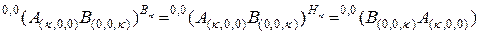. (2.10.14)

Приведенные формулы (2.10.1), (2.10.10) – (2.10.14) не исчерпывают всех возможных случаев. Докажем еще две теоремы о транспонировании произведений многомерных матриц.

Теорема 2.5 (о транспонировании 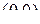-свернутого произведения соответственно произвольной подстановке). Если  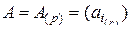– 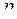-мерная матрица -го порядка, 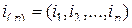 – 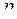-мультииндекс, и  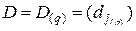– 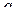-мерная матрица -го порядка, 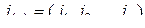 – 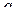-мультииндекс, то

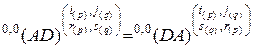,                                  (2.10.15)

где 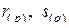 – мультииндексы, образующие вместе некоторую перестановку индексов мультииндексов .

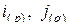Для доказательства формулы (2.10.15) введем обозначения

, ,

, ,

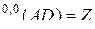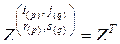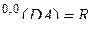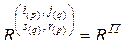из которых следуют равенства для элементов матриц

,

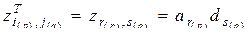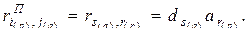
Видно, что 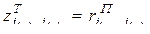, или . Теорема доказана.

Пример 2.8. Пусть 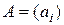 – одномерная матрица второго порядка,

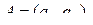
и 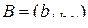 – трехмерная матрица второго порядка,

.

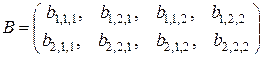На основании формулы (2.10.15) для этих матриц можно записать, что

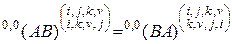.                            (2.10.16)

Проверим правильность этого равенства путем расчетов его левой и правой частей и сравнения их между собой. Для левой части получим

,

 

.

 

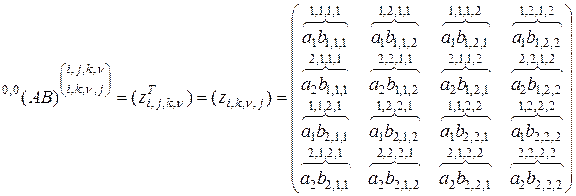Для правой части равенства (2.10.16) будем иметь

,

.

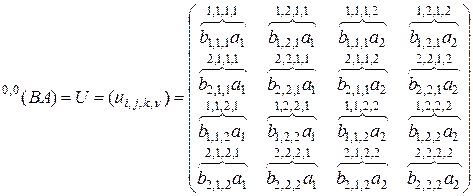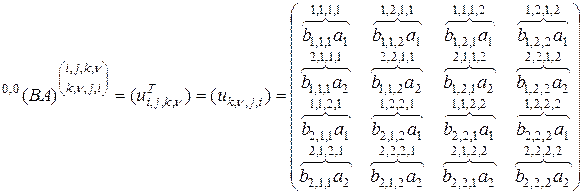Видим, что правая и левая части равенства (2.10.16) совпадают, что подтверждает справедливость формулы (2.10.15).

Теорема 2.6 (о 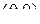-свернутом умножении транспонированных матриц). Если  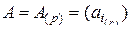– -мерная матрица -го порядка, 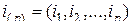, и 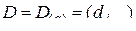 – 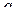-мерная матрица -го порядка, 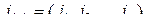, то

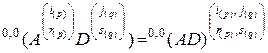,                    (2.10.17)

где 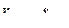 – мультииндексы, представляющие собой некоторые перестановки индексов мультииндексов  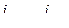соответственно.

Для доказательства равенства (2.10.17) обозначим

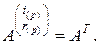
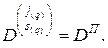
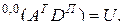
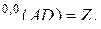
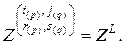
Тогда для элементов матриц можно записать

.

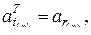
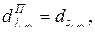
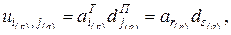
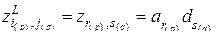Мы видим, что 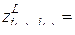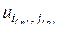, т. е. 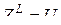, что и доказывает теорему 2.6.

Пример 2.9. Пусть 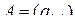 – двухмерная матрица второго порядка,

,

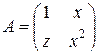и 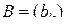 – одномерная матрица второго порядка,

.

По формуле (2.10.17) для этих матриц получим

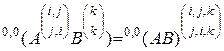.                                  (2.10.18)

Проверим это равенство путем расчетов. Для левой части равенства (2.10.18) находим

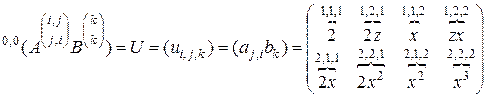. (2.10.19)

Правая часть равенства (2.10.18) определяется выражением

,

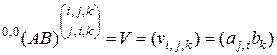что дает предыдущий результат (2.10.19).

Сделаем замечание относительно формулы (2.10.17). Она применима в прямом направлении, т. е. при переходе от матрицы 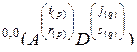 к матрице 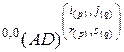. В обратном направлении она применима лишь тогда, когда подстановка  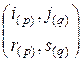разбивается на две подстановки 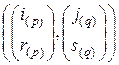. Например, для произведения 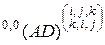, где  – двухмерная матрица, а 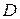 – одномерная, обратный переход невозможен, так как при разбиении подстановки

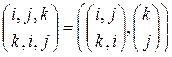
ее составляющие 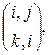 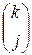подстановками не являются.

При транспонировании многомерных матриц в случаях, не подпадающих под изложенные выше теоремы, приходится прибегать к поэлементной записи матриц.

 

2.11. Некоторые свойства 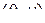-единичной матрицы

 

Установим некоторые свойства 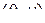-единичной матрицы -го порядка 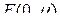, которые будут использоваться в дальнейшем.

Теорема 2.7. Матрица 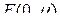 симметрична относительно подстановок  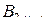или 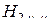, т.е.

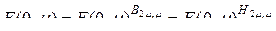.                (2.11.1)

Матрица 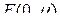 может быть получена возведением в 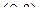-свернутую 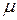-ю степень двухмерной единичной матрицы 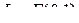, а именно,

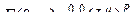,                                    (2.11.2)

где подстановка 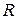 имеет вид

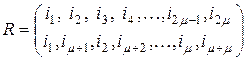.                         (2.11.3)

Действительно, по определению 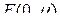 – 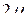-мерная гиперквадратная матрица,

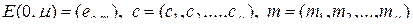,  (2.11.14)

в которой каждый элемент 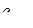 равен символу Кронекера ,

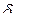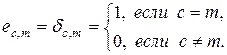                             (2.11.15)

Непосредственно из определения (2.11.15) видно, что

,

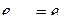т. е. матрица 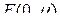 симметрична относительно подстановок  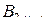или 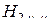. Равенство (2.11.1) доказано. Докажем теперь равенство (2.11.2). Раскроем мультииндексы  в (2.11.15) и запишем левую часть равенства (2.11.2) в развернутом виде

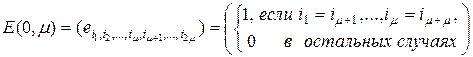. (2.11.19)

Рассмотрим теперь правую часть (2.11.2), для чего раскроем матрицу :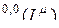

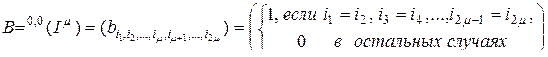. (2.11.20)

Транспонируя матрицу 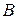 (2.11.20) соответственно подстановке (2.11.3), получим

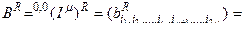
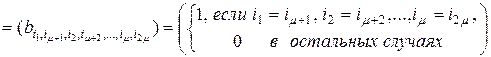. (2.11.21)

Правые части выражений (2.11.19) и (2.11.21) совпадают, следовательно равны и левые их части. Равенство (2.11.2) доказано.

Следствие. 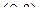-свернутая 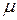-я степень двухмерной единичной матрицы  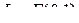может быть представлена в виде

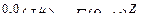,                                    (2.11.22)

где подстановка 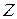 имеет вид

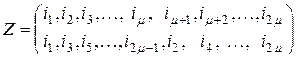.              (2.11.23)

Результат (2.11.22) получаем транспонированием обеих частей равенства (2.11.2) соответственно подстановке 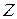 (2.11.23) с учетом правила повторного транспонирования матрицы (2.9.13):

.

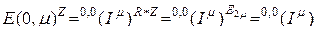Здесь 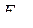 – тождественная подстановка. В том, что подстановк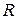и  и 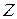 взаимно обратные, т.е. 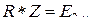, легко убедиться, найдя их суперпозицию.

МНОГОМЕРНО-МАТРИЧНЫЙ АНАЛИЗ

 

В данном разделе анализируется состояние существующих подходов к теории матричного дифференцирования и разрабатывается теория многомерно-матричного дифференцирования.