В функциональном анализе [18,25,27,77,103] многомерные матрицы не нашли отражения. Привычными в анализе являются лишь понятие обычной (двухмерной) матрицы и вектора. Вместе с тем и теория многомерных матриц [81] развивалась без достаточной ориентации на функциональный анализ. В данном разделе выясняются связи между функциональным анализом и теорией многомерных матриц. В частности, устанавливается, что многомерно-матричный анализ применительно к векторным евклидовым пространствам представляет собой конечномерную реализацию (координатную форму [10,11]) функционального анализа.

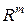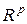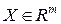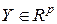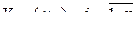Пусть  и  – два евклидовых пространства,  и   – элементы этих пространств. Определим произведение элементов , и , как 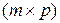-матрицу

.                          (3.3.1)

Матрица 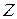 (3.3.1) представляет собой 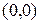-свернутое произведение матриц  и :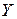

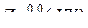.                                              (3.3.2)

Можно говорить также о квадрате элемента 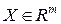 как 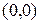-свернутом произведении матриц  и ,

,

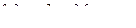и вообще о любой -й 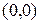-свернутой степени элемента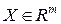

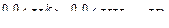,                                     (3.3.3)

которая является -мерной матрицей 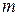-го порядка.

Многомерные матрицы можно отождествлять с мультилинейными отображениями. Действительно, линейное отображение евклидова пространства 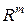 в евклидово пространство  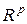имеет вид

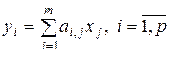,                                    (3.3.4)

т.е. задается двухмерной матрицей

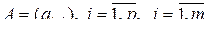.                             (3.3.5)

Отображение (3.3.4) принято записывать в векторно-матричной форме

,

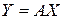где 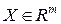,  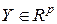– векторы-столбцы. В многомерно-матричных обозначени-

ях выражение (3.3.4) записывается в виде

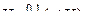.                                              (3.3.6)

Множество всех линейных отображений вида (3.3.4) обозначается 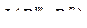 и имеет структуру нормированного векторного пространства [103].

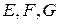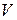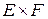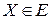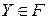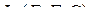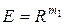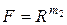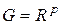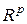Пусть  – векторные пространства. Отображение  пространства  в пространство  называется билинейным, если при фиксировании одной из переменных  или  оно линейно относительно другой переменной. Множество билинейных отображений  имеет структуру нормированного векторного пространства [103]. В случае конечномерных евклидовых пространств , ,  билинейное отображение произведения  в  определяется формулой [27]

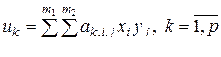,                                 (3.3.7)

где , , 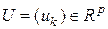. Из выражения (3.3.7) ясно, что любое билинейное отображение пространства  в пространство 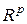 задается трехмерной матрицей

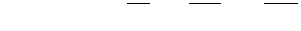.                     (3.3.8)

Учитывая введенное выше произведение векторов (3.3.2), получим для билинейного отображения (3.3.7) удобную многомерно-матричную запись

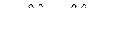,                                            (3.3.9)

где  – матрица (3.3.8). Если в (3.3.9) векторы  и 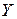 принадлежат одному и тому же пространству 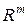, и совпадают, то мы получим квадратичное отображение  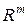в 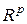 и его многомерно-матричную запись

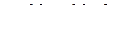,                                        (3.3.10)

или полином второй степени векторной переменной .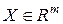

Пусть 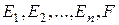 – векторные пространства. Отображение  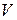простран-

ства 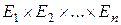 в пространство  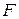называется мультилинейным (или -линейным), если при фиксировании 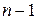 переменных в произвольных  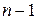векторных пространствах это отображение является линейным относительно оставшейся -й переменной. Множество -линейных отображений из 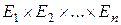 в 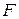 имеет структуру нормированного векторного пространства [103]. По аналогии с билинейным отображением сделаем заключение, что -линейное отображение пространства  в пространство 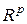 задается 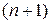-мерной матрицей

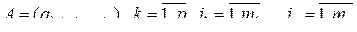,                   (3.3.11)

и имеет вид

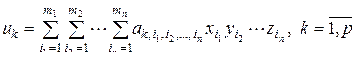,              (3.3.12)

где 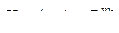, ,…, , 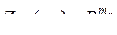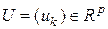. Мультилинейное отображение (3.3.12) можно записать в виде

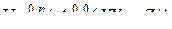.                                 (3.3.13)

Если в выражении (3.3.13) векторы 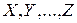 принадлежат одному и тому же пространству 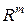, и совпадают, то мы получим отображение -й степени пространства 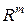 в пространство ,

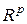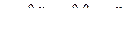,                                         (3.3.14)

или полинома -й степени векторной переменной .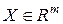

Билинейное отображение пространства 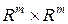 в пространство  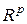задается симметричной относительно перестановки индексов  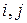трехмерной матрицей (3.3.8) с 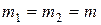. Мультилинейное отображение  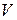пространства  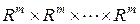в пространство  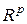называется симметричным, если при любой перестановке элементов множества  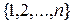и любой системе векторов  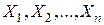из 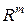 имеют место равенства [103]

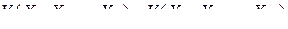.                            (3.3.15)

Из выражения (3.3.13) заключаем, что симметричное мультилинейное отображение задается симметричной относительно индексов 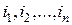 матрицей  (3.3.11) с .

Производная 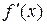, , 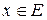отображения  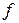банахова пространства  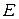в банахово пространство  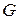(производная Фреше) определена в функкциональном анализе как линейное отображение [103],

,

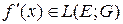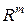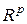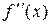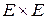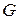и в случае отображения  в  является, таким образом, двухмерной матрицей  (3.3.5). Производная второго порядка  является билинейным симметричным отображением  в  [103],

,

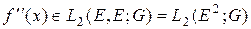и в случае отображения 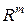 в 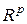 представляется трехмерной матрицей  вида (3.3.8) с 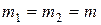, симметричной относительно индексов 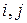. При отображении  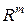в 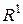 это квадратная симметричная матрица. Вообще, производная -го порядка  является -линейным симметричным отображением 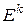 в 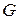 [103],

,

и в случае отображения 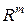 в 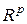 представляется 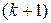-мерной матрицей  вида (3.3.11) с , симметричной относительно индексов . При отображении 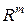 в 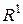 производная -го порядка  представляется -мерной симметричной матрицей 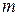-го порядка.

Выводы

В разделе 3 выполнен анализ существующих подходов к двухмерно-матричному и многомерно-матричному дифференцированию и выявлены их ограничения и недостатки. Скалярно-матричное дифференцирование обладает теми ограничениями, что не выходит за рамки двухмерных матриц и, как следствие, не допускает повторного дифференцирования в форме производных, что приводит к трудностям в представлении функций рядами Тейлора, к неестественному определению дифференциала функции. Различные определения матрично-матричных производных также не выходят за рамки теории обычных (двухмерных) матриц. С этой целью в них используются кронекеровские произведения или векторные упорядочивания, что приводит к громоздкости и плохой формализованности таких производных. Известные результаты в области многомерно-матричного дифференцирования также громоздки, плохо формализованы, плохо согласуются с существующей теорией многомерных матриц, в связи с чем не получают дальнейшего развития. В разделе 3 разработана теория многомерно-матричного дифференцирования, свободная от указанных недостатков. В частности:

1) дано определение многомерно-матричной производной (3.2.3);

2) получены основные правила многомерно-матричного дифференцирования: дифференцирование сложной функции (3.2.4), (3.2.5), 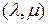-свернутого произведения матриц (3.2.6), неявной функции (3.2.18), (3.2.21), транспонированной матрицы (3.2.22);

3) получены производные ряда многомерно-матричных функций: постоянной матрицы  по  (3.2.23), многомерной матрицы  по  (3.2.25), однородных многомерно-матричных полиномов 1-й степени (3.2.26), 2-й степени (3.2.30), (3.2.31), 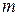-й степени (3.2.38), (3.2.43)–(3.2.47), 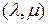-обратной матрицы  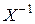по  (3.2.48), 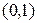-обратной двухмерной матрицы  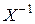по  (3.2.50), определителя двухмерной матрицы  по  (3.2.51) и по 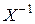  (3.2.52), логарифма определителя двухмерной матрицы  по  (3.2.56) и по 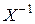  (3.2.57), евклидовой нормы многомерной матрицы  по  (3.2.58);

4) получено представление многомерно-матричной функции многомерно-матричным рядом Тейлора (3.2.61) и многомерно-матричная формула Тейлора (3.2.65);

5) дано определение полного дифференциала многомерно-матричной функции (3.2.66);

6) разработана теория дифференцирования функций симметричных двухмерных матриц (раздел 3.3), симметричных многомерных матриц (раздел 3.4), симметричных относительно множества мультииндексов многомерных матриц (раздел 3.5);

7) установлены соотношения между многомерно-матричным анализом и функциональным анализом (раздел 3.3).