В разделах 2.6, 2.7 выполнен анализ многомерно-матричных линейных алгебраических уравнений с матрицами общего вида и симметричными матрицами и дано обоснование подходов к их численному решению.

Рассмотрим сначала многомерно-матричное уравнение

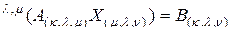,                                     (2.6.1)

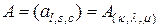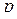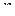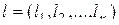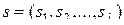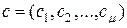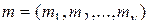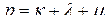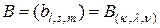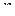где  – -мерная матрица -го порядка общего вида (несимметричная матрица), , , , , ,  – ( )-мерная матрица -го порядка общего вида,  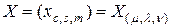– неизвестная ( 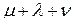)-мерная матрица 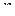-го порядка.

Будем рассматривать случай, когда число уравнений в (2.6.1) равно числу неизвестных, что будет при условии 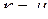. Это значит, что мы рассматриваем матрицу коэффициентов 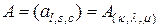, у которой мультииндексы  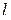и 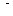 содержат одинаковое число индексов.

Решение уравнения (2.6.1) можно получить с помощью обратной матрицы. Для этого умножим слева обе части уравнения (2.6.1) на левую обычную 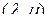-обратную матрицу  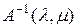в смысле 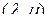-свернутого произведения,

.

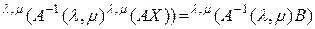Учитывая свойство (2.2.18) 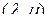-свернутого произведения, получим

.

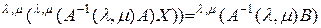С учетом свойства (2.5.2) взаимно обратных обычных матриц будем иметь

,

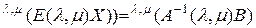а с учетом свойства (2.4.5) единичной обычной матрицы 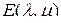 получим сле-

дующее решение уравнения (2.6.1) на основе обратной матрицы [81]:

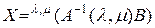.                                        (2.6.2)

Другой подход к решению уравнения (2.6.1) состоит в применении методов, известных для решения двухмерно-матричных линейных алгебраических уравнений, например, метода исключения Гаусса. Этот подход основывается на понятии двухмерной матрицы, ассоциированной с многомерной матрицей. Теорема 2.2 раздела 2.3 о ассоциированных матрицах позволяет утверждать, что многомерно-матричному уравнению (2.6.1) эквивалентно следующее двуxмерно-матричное уравнение, составленное из матриц, ассоциированных к соответствующим матрицам многомерно-матричного уравнения:

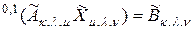.                               (2.6.3)

Решение многомерно-матричного уравнения (2.6.1) можно выполнить следующим образом. Вместо уравнения (2.6.1) будем решать эквивалентное уравнение (2.6.3) известными методами, например, методом исключения Гаусса. Чтобы выполнить такое решение, необходимо для исходных многомерных матриц получить ассоциированные с ними двухмерные матрицы, решить уравнение (2.6.3), и по полученному решению в виде двухмерной матрицы получить решение в виде многомерной матрицы. В действительности получать ассоциированные матрицы нет необходимости. Переход от многомерных матриц к ассоциированным и наоборот состоит в преобразовании значений мультииндексов в значения индексов и наоборот. Поэтому применяемый для решения уравнения (2.6.3) двухмерно-матричный алгоритм необходимо модифицировать, включив в него указанные преобразования значений мультииндексов и индексов.