В данном разделе дано обоснование понятий единичных многомерных матриц в классах матриц общего вида и симметричных матриц. Выяснены недостатки существующего понятия 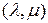-единичной многомерной матрицы при работе с симметричными многомерными матрицами – несимметричность относительно крайних мультииндексов. Это не позволяет использовать такие матрицы при работе с симметричными многомерными матрицами. Дано обоснование и определение симметричной 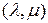-единичной многомерной матрицы, не имеющей указанных недостатков. Это устраняет имеющиеся в теории многомерных матриц ограничения на работу с многомерными симметричными матрицами.

  Рассмотрим многомерно-матричное уравнение

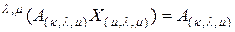,                            (2.4.1)

где

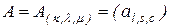 –                                     (2.4.2)

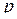-мерная матрица 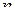-го порядка,

 –

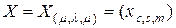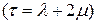-мерная неизвестная матрица того же порядка, причем

, , , ,

.

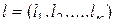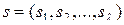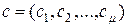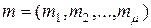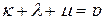В развернутой форме уравнение (2.4.1) имеет вид

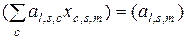.                                     (2.4.3)

Решение 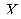 уравнения (2.4.1) (или (2.4.3)) обозначается как  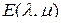и называется 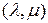-единичной матрицей порядка  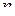[81]. Эта матрица определяется выражением

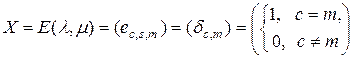.                     (2.4.4)

Легко убедиться, что для любой 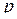-мерной матрицы 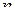-го порядка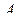

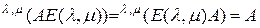.                              (2.4.5)

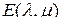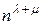Число единиц в матрице  равно . В частности, в матрице  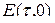все элементы равны единице. Матрица 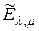, 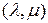-ассоциированная с 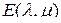, является единичной двухмерной матрицей порядка  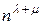[81].

Известная в теории двухмерных матриц единичная матрица, обозначаемая как 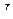, – это матрица  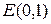в многомерно-матричных обозначениях.

Для симметричной матрицы 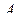 существует также другая матрица 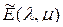, удовлетворяющая уравнению (2.4.1). Определим ее.

Пусть в уравнении (2.4.1) (или (2.4.3)) матрица 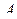 (2.4.2) симметрична относительно мультииндекса 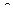. Найдем решение  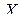в этом случае. Для этого рас-

смотрим произведение в левой части уравнения (2.4.1), т.е. выражение

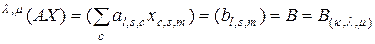,                         (2.4.6)

в котором суммирование ведется по всем значениям мультииндекса 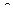. Зафиксируем значение  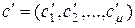мультииндекса 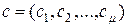, 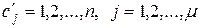. Пусть в  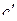значение  повторяется 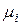 раз, 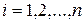. Тогда в сумме в (2.4.6) будет содержаться сумма

,

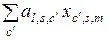где суммирование ведется по всем перестановкам значений мультииндекса 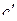. Поскольку это перестановки с повторениями, то их число равно

.

В силу указанной симметрии матрицы 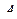 ее элементы  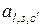будут равны между собой, и предыдущая сумма примет вид

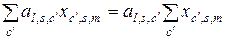.                                   (2.4.7)

Выбрав здесь 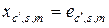, где 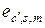 подчиняется условиям (2.4.4), получим

,

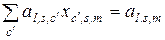или

.

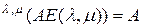Это значит, что матрица 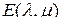 является единичной и для симметричной относительно  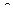матрицы 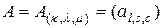. Еще одну единичную матрицу можно получить, если предположить, что матрица  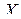также симметрична относительно мультииндекса 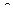. В это случае все слагаемые вида  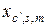в правой части выражения (2.4.7) будут равными между собой, и мы получим

.

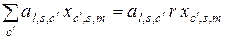Если выбрать 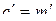 и

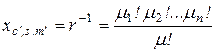,                                   (2.4.8)

где 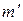 – конкретное значение мультииндекса 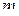, то мы получим

.

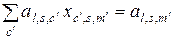Последнее выражение свидетельствует о том, что мы можем удовлетворить уравнению (2.4.3), учитывая только элементы матрицы 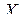  вида (2.4.8) и не учитывая (обнуляя) остальные элементы этой матрицы. Мы получили следующий результат. Решением уравнения (2.4.1) (или (2.4.3)) с симметричной относительно мультииндекса  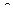матрицей  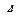(2.4.2) является матрица

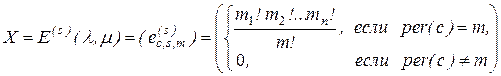, (2.4.9)

где 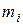 – число повторений значения  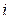в мультииндексе  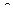(или 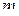), , ,  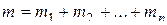– любая перестановка индексов в 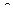. Эту матрицу  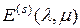назовем правой симметричной 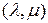-единичной матрицей порядка 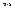. Эта матрица является симметричной относительно индексов мультииндексов 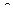, , 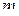а также относительно перестановки этих мультииндексов.

Заметим, что "обычная" единичная матрица 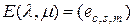 симметрична относительно перестановки своих мультииндексов 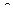, , 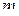но несимметрична относительно этих мультииндексов в отдельности. Заметим также, что для выполнения равенства

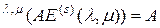
матрица 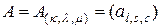 может быть несимметричной относительно своего свободного мультииндекса 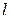, и число индексов в мультииндексах 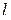,  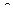не обязано быть одним и тем же.

Аналогичным образом можно определить левую симметричную 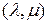-единичную матрицу 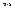-го порядка для любой 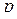-мерной матрицы 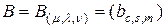, симметричной относительно кэлиевого мультииндекса 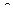, как матрицу, удовлетворяющую равенству

,

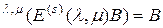Эта матрица определяется выражением, аналогичным выражению (2.4.9), т.е.

.

Левая и правая симметричные единичные матрицы 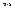-го порядка для одной и той же 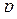-мерной матрицы 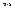-го порядка  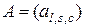будут в общем случае различными хотя бы потому, что мультииндексы  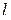и 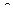 могут содержать различное число индексов. Для такой матрицы могут существовать правая и левая единичные матрицы различных размерностей  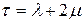(при различных значениях  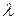и 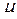). 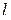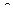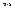Если же мультииндексы  и  симметричной относительно индексов этих мультииндексов -мерной матрицы -го порядка  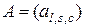содержат одинаковое число индексов, то правая единичная матрица  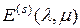будет также и левой единичной матрицей, т.е. будут выполняться равенства

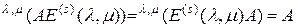.                                 (2.4.10)

В этом случае матрицу 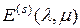 будем называть просто симметричной 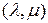-единичной матрицей 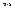-го порядка. Понятно, что указанное тождество (2.4.10) будет выполняться также для любой вполне симметричной 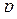-мерной матрицы 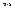-го порядка вида .

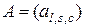Рассмотрим также 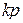-мерную симметричную относительно своих -мультииндексов 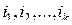 матрицу 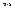-го порядка

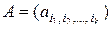.                                     (2.4.11)

Представим ее в виде

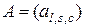,                                         (2.4.12)

где 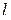 – 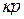-мультииндекс,  – 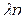-мультииндекс,  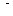– 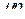-мультииндекс, 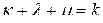, и предположим, что 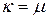. Матрицу 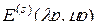, удовлетворяющую равенству

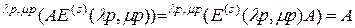,               (2.4.13)

будем называть симметричной по мультииндексам 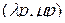-единичной матрицей. Это 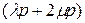-мерная матрица Она, очевидно, определяется выражением

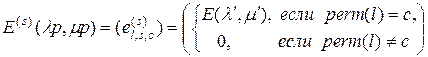,            (2.4.14)

где 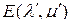 – обычная 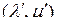-единичная 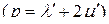-мерная матрица. Если же матрицу  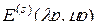определить выражением

,       (2.4.15)

где 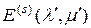 – симметричная 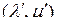-единичная 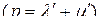-мерная матрица, то это будет полностью симметричная 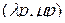-единичная матрица. В этом случае равенство

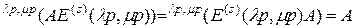
будет выполняться для вполне симметричной матрицы 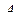 вида (2.4.12).