Над многомерными матрицами можно выполнять операции сложения, умножения, умножения на число.

Сложение двух 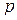-мерных матриц с одинаковыми размерами по каждому измерению сводится к сложению их соответствующих элементов. Так, если

,

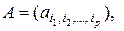
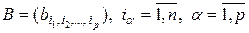то

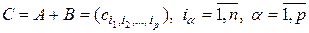,                      (2.2.1)

где

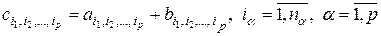.            (2.2.2)

Если 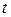 – некоторое число,  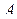– 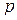-мерная матрица 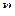-го порядка, то произведение  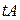есть матрица

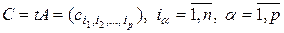,                    (2.2.3)

элементы которой определяются формулой

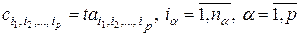.                  (2.2.4)

Рассмотрим операцию умножения многомерных матриц. Пусть 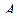 – 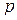-мерная матрица 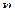-го порядка,

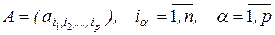,                          (2.2.5)

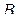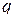 – -мерная матрица 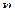-го порядка,

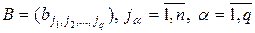.                          (2.2.6)

Разобьем мультииндексы 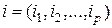,  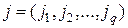на составляющие мультииндексы следующим образом:

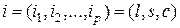,                                  (2.2.7)

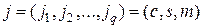,                                (2.2.8)

где

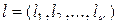,                                         (2.2.9)

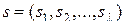,                                       (2.2.10)

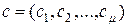,                                      (2.2.11)

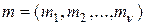                                    (2.2.12)

и

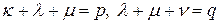.                              (2.2.13)

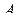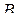Тогда матрицы  и  (2.2.5), (2.2.6) можно записать в виде

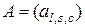,                                             (2.2.14)

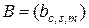,                                             (2.2.15)

где каждый из индексов мультииндексов 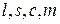 пробегает значения от 1 до .

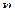Матрица

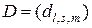
называется 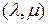-свернутым произведением матриц  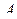и 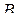, если ее элементы определяются выражением

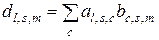.                                     (2.2.16)

Обозначается 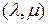-свернутое произведение как 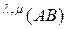. Таким образом,

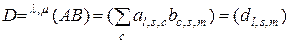.                        (2.2.17)

В произведении (2.2.17) мультииндекс 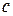 (2.2.11), по которому производится суммирование, называется кэлиевым, мультииндекс  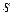(2.2.10), общий для множителей и произведения, – скоттовым, а мультииндексы  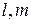(2.2.9), (2.2.12), не причастные к свертыванию, – свободными.

Пример 2.3. Рассмотрим две трехмерные матрицы второго порядка

, .

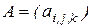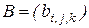
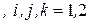Тогда 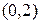-свернутое произведение  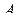на 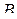 будет двухмерной матрицей второго порядка

, .

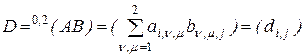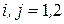Ее элементы рассчитываются по формулам

,

,

,

.

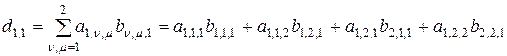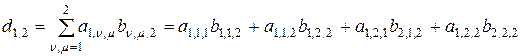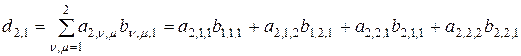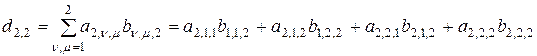В частности, если

,

.

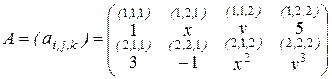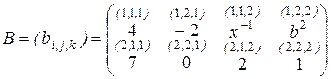то

,

,

,

.

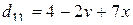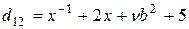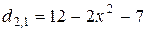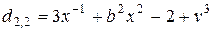Из определения 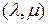-свернутого произведения матриц  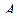и 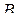 следует, что в общем случае оно не обладает коммутативным свойством, т.е. в общем случае

.

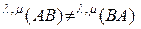Выполняется дистрибутивный закон умножения матриц одного и того же порядка относительно сложения матриц одного и того же числа измерений:

.

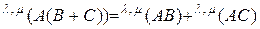Есл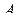и 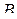 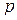и  – - и 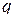-мерные матрицы 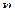-го порядка вида (2.2.14), (2.2.15) и числа  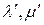удовлетворяют условию

,

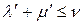то выполняется ассоциативный закон умножения матриц

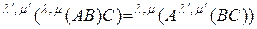.                          (2.2.18)

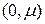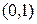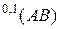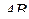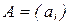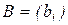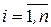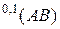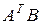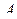Большое распространение имеет -свернутое произведение. Так, многомерно-матричное -свернутое произведение  совпадает с известным произведением  двухмерных матриц. В частности, если , , , – одномерные матрицы (векторы в векторно-матричном подходе), то  совпадает с произведением , где  и 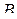 понимаются как векторы-столбцы. Мы видим, что в многомерном матричном подходе нет необходимости различать вектор-столбец и вектор-строку.

Произведению скалярных величин соответствует 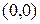-свернутое произведение многомерных матриц, поэтому вместо  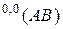мы будем писать 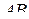. В частности, если 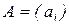, , 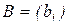, 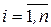– одномерные матрицы (векторы), то  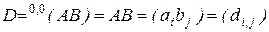– двухмерная матрица. Это произведение совпадает с произведением  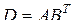векторно-матричного подхода, где 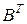– вектор-строка, а  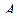– вектор столбец.

Любую матрицу 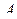, представленную в виде (2.2.14), будем обозначать также 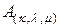, где числа 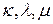, , 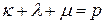указывают на количество свободных, скоттовых и кэлиевых индексов матрицы  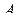соответственно. Так, обозначение  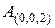свидетельствует, что двухмерная матрица  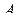содержит только кэлиевы индексы.