Определение. Многомерной ( 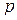-мерной ) 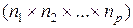-матрицей называется система чисел или переменных 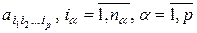, расположенных в точках 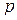-мерного пространства, определяемого координатами  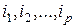[81].

Обозначается 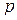-мерная матрица следующим образом:

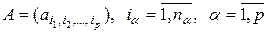.                             (2.1.1)

В случае различных чисел 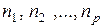 матрица называется гиперпрямоугольной. Если 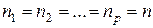, то матрица называется гиперквадратной или 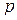-мерной матрицей -го порядка.

Совокупность индексов 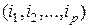 многомерной матрицы будем называть мультииндексом и обозначать одним символом 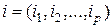. Для того, чтобы указать количество индексов в мультииндексе, будем применять также обозначение 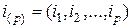. Мультииндекс, содержащий  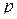индексов, будем называть 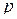-мультииндексом. С применением мультииндексов многомерную матрицу (2.1.1) будем обозначать также

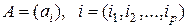.                                  (2.1.2)

Многомерную матрицу можно изобразить в виде двухмерной (плоской) матрицы. Для этого достаточно разбить множество ее индексов на два множества и упорядочить каким-либо образом значения индексов этих множеств.

Пример 2.1. Рассмотрим трехмерную матрицу второго порядка

.

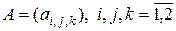Разбивая множество индексов этой матрицы на два множества 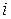 и 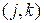 и упорядочивая значения этих множеств в виде (1,2) и ((1,1),(2,1),(1,2),(2,2)), эту матрицу можно изобразить в виде следующей двухмерной матрицы

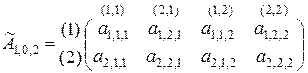.                     (2.1.3)

Строки этой матрицы нумеруются одним числом, записанным перед открывающей скобкой, а столбцы – парой чисел, записанной над матрицей. Матрица имеет другое обозначение 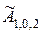, поскольку в отличие от  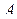это двухмерная матрица. Однако она полностью представляет матрицу 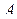, так как содержит все ее элементы. Смысл обозначения  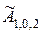поясняется в разделе 2.3.

Многомерная матрица 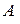 (2.1.1) называется симметричной относительно двух своих индексов 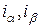, если каждые два ее элемента, получающиеся один из другого перестановкой этих индексов, одинаковы, т.е. если

.

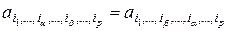Многомерная матрица 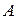 (2.1.1) называется симметричной относительно нескольких индексов, если она симметрична относительно любой пары из них.

Многомерная матрица 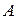 (2.1.1) называется просто симметричной, если она симметрична относительно всех своих индексов.

Число 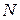 отличающихся друг от друга элементов симметричной 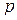-мерной

 матрицы 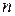-го порядка подсчитывается по формуле

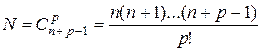.                            (2.1.4)

При этом каждый элемент симметричной матрицы повторяется 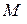 раз [61],

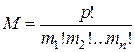,                                        (2.1.5)

где 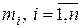, – количество значений 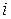, встречающихся в мультииндексе, .

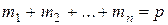Пример 2.2. Рассмотрим симметричную трехмерную матрицу второго порядка

.

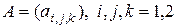Она имеет 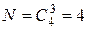 различных элемента: 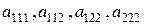. Элементы  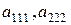повторяются по одному разу, а элементы  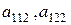– по 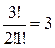 раза. Эта матрица, представленная в виде двухмерной матрицы, имеет следующий вид:

.

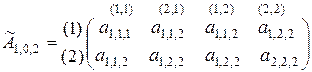Одинаковые элементы здесь обозначены одинаковыми значениями индексов.

Элементы многомерной матрицы, у которых значения всех индексов одинаковы, называются диагональными (лежащими на главной диагонали).

Многомерная матрица, у которой все элементы, расположенные вне главной диагонали, равны нулю, называется диагональной. Диагональную матрицу будем обозначать как .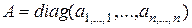

Если все элементы многомерной матрицы 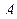 равны нулю, то матрица называется нулевой и обозначается как .

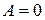Рассмотрим также 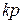-мерную матрицу 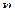-го порядка

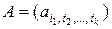,                                              (2.1.6)

где 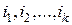 – 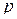-мультииндексы. Эту матрицу назовем симметричной относительно своих мультииндексов, если она не изменяется при перестановке местами любой пары мультииндексов.