Векторно-матричный подход базируется на векторных и матричных представлениях. Отдельные скалярные переменные группируются (упорядочиваются) в наборы, которые называются векторами и матрицами. Теоретическую основу векторно-матричного подхода составляет теория матриц [7, 12, 37] и матричный анализ [19, 101, 108, 110, 123].
Основные понятия теории матриц
Матрицей размера 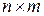 (двухмерной матрицей) называется набор чисел или
(двухмерной матрицей) называется набор чисел или
переменных, упорядоченных по строкам и столбцам в виде таблицы
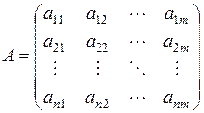 .
.
Коротко матрица обозначается как
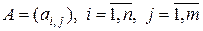 .
.
В общем случае 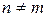 матрица называется прямоугольной, а при
матрица называется прямоугольной, а при 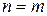 – квадратной или матрицей
– квадратной или матрицей 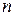 -го порядка. Матрица
-го порядка. Матрица
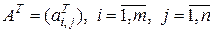 ,
,
элементы которой определяются по формуле
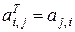 ,
,
называется транспонированной относительно 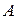 .
.
Матрица  , совпадающая со своей транспонированной матрицей, т.е. удовлетворяющая равенству
, совпадающая со своей транспонированной матрицей, т.е. удовлетворяющая равенству 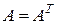 , называется симметричной.
, называется симметричной.
Матрицу, состоящую из одного столбца, называют вектором-столбцом,
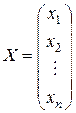 .
.
По определению принимается, что транспонированный вектор-столбец 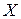 представляет собой вектор-строку,
представляет собой вектор-строку,

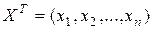 .
.
Для матриц определены операции умножения на число и сложения.
Суммой матриц 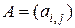 , и
, и 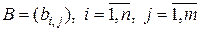 , называется матрица
, называется матрица 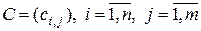 , элементы которой определяются формулой
, элементы которой определяются формулой
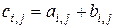 .
.
Сумма матриц обозначается как
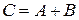 .
.
Произведением матрицы  , на число
, на число  называется матрица
называется матрица 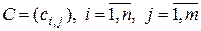 , элементы которой определяются формулой
, элементы которой определяются формулой
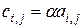 .
.
Произведение матрицы на число обозначается
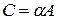 .
.
Матрица  , все элементы которой равны нулю, называется нулевой и обозначается
, все элементы которой равны нулю, называется нулевой и обозначается 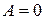 . Матрица
. Матрица 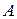
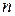 -го порядка, элементы которой определяются равенством
-го порядка, элементы которой определяются равенством
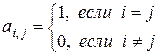 ,
,
называется единичной и обозначается  .
.
Рассмотрим пространство всевозможных  -матриц с введенными на нем вышеописанными операциями сложения и умножения на число. Легко видеть, что эти операции обладают следующими свойствами:
-матриц с введенными на нем вышеописанными операциями сложения и умножения на число. Легко видеть, что эти операции обладают следующими свойствами:
§ 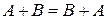 (коммутативность);
(коммутативность);
§ 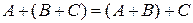 (ассоциативность);
(ассоциативность);
§ 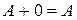 (существование нулевого элемента
(существование нулевого элемента  );
);
§ 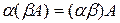 ;
;
§ 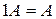 ;
;
§ 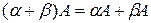 ;
;
§ 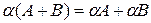 .
.
Отсюда мы видим, что множество прямоугольных матриц образует линейное
пространство.
Произведением  -матрицы
-матрицы 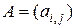 на
на  -матрицу
-матрицу  называется
называется 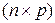 -матрица
-матрица 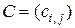 , элементы которой определяются как
, элементы которой определяются как
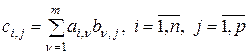 .
.
Произведение матриц обозначается
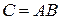 .
.
Частными случаями этого произведения являются скалярное и тензорное произведения векторов. Если 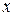 и
и 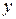 – векторы, содержащие по
– векторы, содержащие по  компонент, то произведение
компонент, то произведение

представляет собой число, называемое скалярным произведением 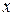 и
и  . Матрица
. Матрица  размера
размера 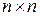 с элементами
с элементами  , называется тензорным произведением этих же векторов [29].
, называется тензорным произведением этих же векторов [29].
Для рассмотренных произведений справедливы следующие правила транспонирования:
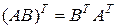 ,
,
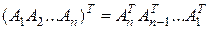 .
.
Известен еще один вид произведения матриц – кронекеровское произведение. В работе [30] это произведение называется прямым и определяется следующим образом. Прямое произведение  матрицы
матрицы  размера
размера 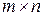 и матрицы
и матрицы 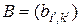 размера
размера 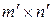 есть матрица
есть матрица
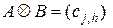 ,
, 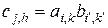 ,
,
размера 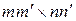 , где индекс
, где индекс 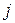 означает порядковый номер пары
означает порядковый номер пары 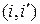 в последовательности
в последовательности 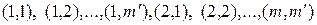 , а индекс
, а индекс  – порядковый номер пары
– порядковый номер пары 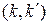 в аналогичной последовательности. В работе [7] приводится сдедующее лучше визуально воспринимаемое определение. Кронекеровское произведение
в аналогичной последовательности. В работе [7] приводится сдедующее лучше визуально воспринимаемое определение. Кронекеровское произведение 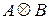 матрицы
матрицы  размера
размера 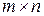 и матрицы
и матрицы 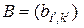 размера
размера 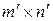 есть матрица размера
есть матрица размера 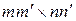 , определяемая формулой
, определяемая формулой
 .
.
Пример 1.16. Если матрицы  и
и 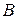 имеют вид
имеют вид
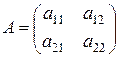 ,
,  ,
,
то их кронекеровским произведением будет матрица
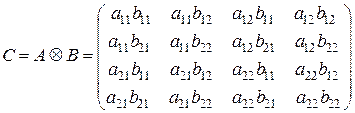 .
.
Для матрицы 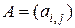
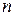 -го порядка определена скалярная функция, которая называется определителем матрицы и обозначается
-го порядка определена скалярная функция, которая называется определителем матрицы и обозначается 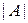 или
или  . Наиболее распространенный способ вычисления определителя матрицы
. Наиболее распространенный способ вычисления определителя матрицы 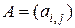 состоит в использовании его разложения по элементам
состоит в использовании его разложения по элементам 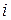 -й строки матрицы:
-й строки матрицы:
 ,
,
где 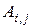 – матрица, которая получается после вычеркивания из исходной матрицы
– матрица, которая получается после вычеркивания из исходной матрицы 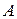
 -й строки и
-й строки и  -го столбца. Числа
-го столбца. Числа 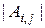 называются минорами матрицы
называются минорами матрицы 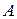 , а числа
, а числа 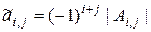 – алгебраическими дополнениями.
– алгебраическими дополнениями.
Для двух квадратных матриц 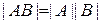 .
.
Матрица 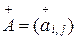
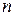 -го порядка называется присоединенной к матрице
-го порядка называется присоединенной к матрице 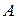
 -го порядка, если она определяется выражением
-го порядка, если она определяется выражением
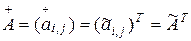 .
.
Матрица 
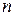 -го порядка называется особенной, вырожденной или сингулярной, если
-го порядка называется особенной, вырожденной или сингулярной, если  .
.
Для невырожденной матрицы 
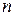 -го порядка существует обратная матрица
-го порядка существует обратная матрица
 .
.
Это такая матрица, которая удовлетворяет равенству 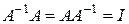 . Обратную матрицу можно получить по формуле
. Обратную матрицу можно получить по формуле
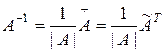 .
.
Справедлива следующая формула транспонирования обратной матрицы:
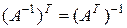 .
.
Если матрица разбита на отдельные матрицы (блоки), то она называется блочной. Практический интерес представляет формула Фробениуса для обращения блочной матрицы. Пусть  – невырожденная квадратная блочная матрица вида
– невырожденная квадратная блочная матрица вида
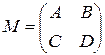 , (1.3.1)
, (1.3.1)
где 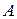 – квадратная невырожденная матрица (
– квадратная невырожденная матрица ( 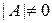 ). Тогда обратная матрица
). Тогда обратная матрица 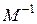 может быть определена по следующей формуле Фробениуса [12]
может быть определена по следующей формуле Фробениуса [12]
 , (1.3.2)
, (1.3.2)
где
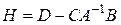 .
.
Если же предположить, что в матрице 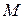 (1.3.1)
(1.3.1)  , то можно получить другой вид формулы Фробениуса
, то можно получить другой вид формулы Фробениуса
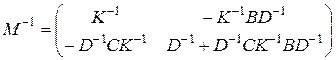 , (1.3.3)
, (1.3.3)
где
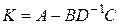 .
.
Прямоугольную матрицу 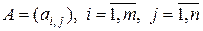 , можно рассматривать как оператор
, можно рассматривать как оператор 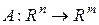 , действующий из
, действующий из 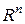 в
в 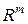 (см. раздел 1.2.2). В случае квадратной матрицы
(см. раздел 1.2.2). В случае квадратной матрицы 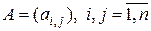 отображение
отображение
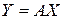
состоит в повороте вектора 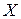 и изменении его длины (нормы). Ненулевые векторы
и изменении его длины (нормы). Ненулевые векторы 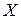 , для которых
, для которых
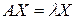 ,
,
называются собственными векторами матрицы 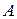 . Из определения собственных векторов ясно, что это такие векторы, которые отображаются матрицей
. Из определения собственных векторов ясно, что это такие векторы, которые отображаются матрицей 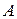 без поворота, а только с изменением их длины. Число
без поворота, а только с изменением их длины. Число  , соответствующее собственному вектору
, соответствующее собственному вектору 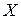 матрицы
матрицы 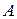 , называется собственным числом или собственным значением матрицы
, называется собственным числом или собственным значением матрицы  . Собственные векторы определяются как ненулевое решение однородного уравнения
. Собственные векторы определяются как ненулевое решение однородного уравнения
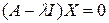 .
.
Такое решение существует, когда
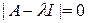 .
.
Собственные числа 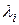 матрицы
матрицы  определяются как решение последнего уравнения.
определяются как решение последнего уравнения.
Как любой оператор, прямоугольная матрица 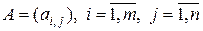 , может иметь норму (см. раздел 1.2.2). Эта норма должна быть согласованной с нормой вектора
, может иметь норму (см. раздел 1.2.2). Эта норма должна быть согласованной с нормой вектора  . С евклидовой нормой вектора
. С евклидовой нормой вектора 

согласована спектральная норма матрицы
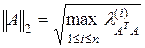 ,
,
где 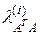 обозначены собственные числа матрицы
обозначены собственные числа матрицы 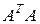 . Норма
. Норма 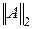 является операторной. С евклидовой нормой вектора согласована также евклидова норма матрицы
является операторной. С евклидовой нормой вектора согласована также евклидова норма матрицы
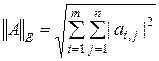 ,
,
которая, однако, не является операторной, поскольку для любой единичной матрицы 
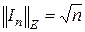 .
.
Векторно-матричный анализ
Если элементы матрицы 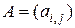 являются функциями скалярной переменной
являются функциями скалярной переменной  ,
, 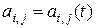 , то говорят, что матрица
, то говорят, что матрица  является функцией скалярного аргумента
является функцией скалярного аргумента 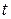 и записывают это в виде выражения
и записывают это в виде выражения  . Производная матричной функции скалярного аргумента определяется равенством
. Производная матричной функции скалярного аргумента определяется равенством
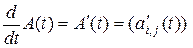 .
.
Аналогичным образом определяется интеграл от матричной функции скалярного аргумента:
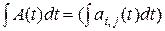 .
.
Таким образом, чтобы продифференцировать или проинтегрировать матричную функцию скалярного аргумента, необходимо продифференцировать или проинтегрировать по этому аргументу все ее элементы.
Более сложным является вопрос дифференцирования скалярной, векторной или матричной функции векторного или матричного аргумента. В работе [2] дается следующее определение производной скалярной функции матричного аргумента: если 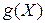 – скалярная функция матричного аргумента
– скалярная функция матричного аргумента  , то производной функции
, то производной функции 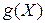 по
по  называется
называется 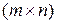 -матрица частных производных
-матрица частных производных
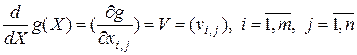 . (1.3.4)
. (1.3.4)
Эта производная в работе [2] названа скалярно-матричной. В соответствии с этим определением производная скалярной функции по вектору-строке является вектором-строкой частных производных, а по вектору-столбцу – вектором-столбцом частных производных.
Если 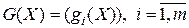 , – векторная функция векторного аргумента, то производная
, – векторная функция векторного аргумента, то производная  по
по 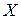 определяется как
определяется как 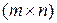 -матрица частных производных
-матрица частных производных
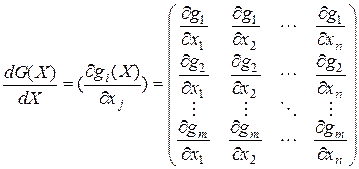 .
.
Эта матрица называется матрицей Якоби.
Практический интерес представляет дифференцирование линейных и квадратичных функций вектора-столбца 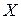 . Если в скалярной линейной функции
. Если в скалярной линейной функции

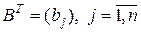 , – вектор-строка коэффициентов, то
, – вектор-строка коэффициентов, то
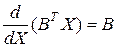 .
.
Если в векторной линейной функции
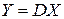
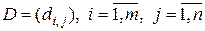 , – матрица коэффициентов, то
, – матрица коэффициентов, то
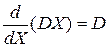 .
.
Для квадратичной формы вектора 
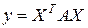
где  , – симметричная квадратная матрица коэффициентов, получены производные
, – симметричная квадратная матрица коэффициентов, получены производные
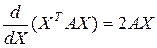 ,
,
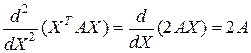 .
.
В работе [2] приведены некоторые скалярно-матричные производные (производные следа, определителя матрицы и др.). Эти производные получены также в разделах 3.2.13 – 3.2.15 данной работы в рамках аппарата многомерно-матричного дифференцирования.
Для дифференцирования матричной функции по матричному аргументу (матрично-матричное дифференцирование) в работе [2] введено понятие дифференциала матрицы: если  – матричная функция от матрицы
– матричная функция от матрицы 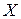 , то дифференциал
, то дифференциал 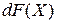 задается в виде
задается в виде
 ,
,
где
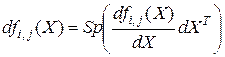 ,
,
и 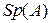 означает след матрицы
означает след матрицы 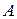 . Как видно, дифференциал матричной функции есть матрица тех же размеров, что и сама функция. Это позволяет авторам работы [2] при матрично-матричном дифференцировании не выходить за рамки обычных (двухмерных) матриц. В работе [2] получены дифференциалы некоторых матричных функций (произведения, степени, обратной матрицы и др.). Необходимо отметить, что нахождение дифференциала не всегда оказывается достаточным. Часто нужно иметь производную. В этом состоит ограничение подхода работы [2]. Кроме того, эта теория относится лишь к обычным (двухмерным) матрицам. Тем не менее этот подход находит в настоящее время применение. Так, некоторые скалярно-матричные производные приводятся в работах [19, 89].
. Как видно, дифференциал матричной функции есть матрица тех же размеров, что и сама функция. Это позволяет авторам работы [2] при матрично-матричном дифференцировании не выходить за рамки обычных (двухмерных) матриц. В работе [2] получены дифференциалы некоторых матричных функций (произведения, степени, обратной матрицы и др.). Необходимо отметить, что нахождение дифференциала не всегда оказывается достаточным. Часто нужно иметь производную. В этом состоит ограничение подхода работы [2]. Кроме того, эта теория относится лишь к обычным (двухмерным) матрицам. Тем не менее этот подход находит в настоящее время применение. Так, некоторые скалярно-матричные производные приводятся в работах [19, 89].
Теория скалярно-матричного дифференцирования позволяет записать три члена ряда Тейлора для скалярной функции 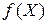 векторной переменной
векторной переменной  :
:
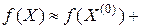
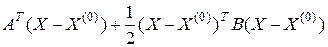 , (1.3.5)
, (1.3.5)
где  – вектор-столбец аргументов функции
– вектор-столбец аргументов функции 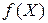 ,
, 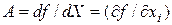 ,
, 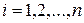 – первая производная функции
– первая производная функции 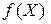 в точке
в точке 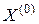 , которая называется градиентам функции
, которая называется градиентам функции 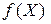 в точке
в точке 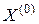 ,
, 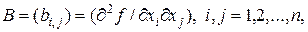 – вторая производная функции
– вторая производная функции 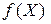 в точке
в точке 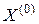 (
( 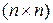 -матрица), которая называется матрицей Гессе в точке
-матрица), которая называется матрицей Гессе в точке 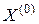 .
.
Записать последующие члены ряда Тейлора с помощью векторно-матричного подхода и теории скалярно-матричного дифференцирования не представляется возможным.
Выводы
Векторно-матричный подход преодолевает большинство недостатков классического подхода. Во-первых, он строго формализован и менее громоздок по сравнению с классическим подходом. Во-вторых, модели, полученные в рамках этого подхода, во многом аналогичны моделям скалярного случая. Поясним это на примере системы рис. 1.2. Если ввести в рассмотрение вектор-столбец входных воздействий 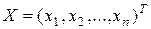 , то векторная модель (1.1.9) нашей системы запишется в виде
, то векторная модель (1.1.9) нашей системы запишется в виде
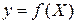 . (1.3.12)
. (1.3.12)
Линейная векторно-матричная модель (1.1.10) системы будет иметь вид
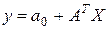 , (1.3.13)
, (1.3.13)
где 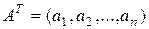 – матрица-строка коэффициентов модели. Квадратичная модель (1.1.11) запишется в виде
– матрица-строка коэффициентов модели. Квадратичная модель (1.1.11) запишется в виде
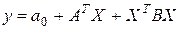 , (1.3.14)
, (1.3.14)
где 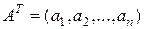 – матрица-строка коэффициентов при линейных членах модели, а
– матрица-строка коэффициентов при линейных членах модели, а 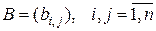 , – квадратная симметричная матрица коэффициентов при квадратичных членах. Мы видим, что выражения (1.3.13), (1.3.14) менее громоздки по сравнению с выражениями (1.1.10), (1.1.11). Кроме того, они аналогичны выражениям (1.1.2), (1.1.3) скалярного случая, т. е. являются их естественными обобщениями.
, – квадратная симметричная матрица коэффициентов при квадратичных членах. Мы видим, что выражения (1.3.13), (1.3.14) менее громоздки по сравнению с выражениями (1.1.10), (1.1.11). Кроме того, они аналогичны выражениям (1.1.2), (1.1.3) скалярного случая, т. е. являются их естественными обобщениями.
Однако векторно-матричный подход имеет и определенные недостатки. Он обладает ограниченными возможностями по представлению нелинейных данных, поскольку с его помощью можно получить не более чем квадратичные модели (1.3.14). Имеются случаи представления моделей третьей и даже четвертой степени [110], однако это скорее исключение, чем общее правило. В связи с этим считается, что матрицы являются “линейными преобразованиями” [7]. Понятие матрично-матричной производной определено лишь в форме дифференциала (раздел 1.3.1), что не всегда достаточно. Попытки использования для определения матрично-матричной производной кронекеровских произведений приводят к ухудшению формализованности подхода, поскольку кронекеровское произведение плохо формализовано. Кроме того, векторно-матричный подход не позволяет работать с многомерными массивами данных, широко применяемыми во всех языках программирования.
Имеются также попытки привлечения к анализу многомерных данных тензорного подхода, сводящегося к использованию тензора в качестве многомерной матрицы и операций внешнего и внутреннего произведения тензоров. Однако такой подход нельзя считать правомерным. Тензор определяется как геометрический объект в 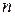 -мерном линейном пространстве
-мерном линейном пространстве  , в то время как многомерная матрица определяется как алгебраический объект в
, в то время как многомерная матрица определяется как алгебраический объект в 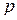 -мерном пространстве своих индексов. Это значит, что тензор не является многомерной матрицей. Общим свойством этих двух объектов является лишь то, что они представляют собой совокупности многоиндексных величин. Вместе с тем все индексы тензора пробегают значения от 1 до
-мерном пространстве своих индексов. Это значит, что тензор не является многомерной матрицей. Общим свойством этих двух объектов является лишь то, что они представляют собой совокупности многоиндексных величин. Вместе с тем все индексы тензора пробегают значения от 1 до 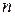 , в то время как индексы многомерной матрицы могут пробегать различное число значений. Это значит, что с использованием тензоров мы не получаем возможности работать с гиперпрямоугольными многомерными матрицами. Использование тензорных произведений также не дает никаких преимуществ, так как операции внешнего и внутреннего произведения тензоров не позволяют реализовать
, в то время как индексы многомерной матрицы могут пробегать различное число значений. Это значит, что с использованием тензоров мы не получаем возможности работать с гиперпрямоугольными многомерными матрицами. Использование тензорных произведений также не дает никаких преимуществ, так как операции внешнего и внутреннего произведения тензоров не позволяют реализовать  -свернутое произведение многомерных матриц при
-свернутое произведение многомерных матриц при  (см. раздел 2).
(см. раздел 2).
Дата: 2019-02-02, просмотров: 666.