Пусть даны два линейных пространства 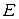 и
и 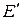 . Если каждому элементу
. Если каждому элементу 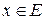 поставлен в соответствие элемент
поставлен в соответствие элемент 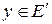 , то говорят, что задано отображение
, то говорят, что задано отображение 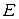 в
в 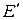 . Это отображение называется также функцией, определенной на
. Это отображение называется также функцией, определенной на 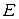 со значениями в
со значениями в 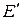 . Любое отображение (или функцию) обозначают
. Любое отображение (или функцию) обозначают
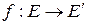 или
или 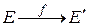 .
.
Запись вида 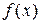 означает элемент из
означает элемент из 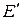 , соответствующий
, соответствующий 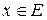 при отображении
при отображении 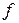 . Числовая функция, заданная на пространстве
. Числовая функция, заданная на пространстве 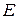 , часто называется функционалом.
, часто называется функционалом.
Отображение 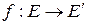 , обладающее свойством
, обладающее свойством
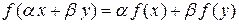 ,
,
где 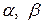 – любые числа, называется линейным. Каждое однородное линейное отображение может быть записано как умножение вектора
– любые числа, называется линейным. Каждое однородное линейное отображение может быть записано как умножение вектора 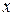 на линейный оператор
на линейный оператор 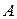 (линейную операцию), т.е. в виде
(линейную операцию), т.е. в виде
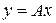 ,
,
причем
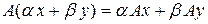 .
.
Функция вида 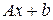 , где
, где 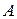 – линейный оператор, называется линейной функцией.
– линейный оператор, называется линейной функцией.
Пространство линейных операторов, действующих из 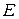 в
в 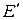 , обозначается
, обозначается 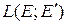 .
.
Если элемент 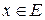 преобразуется в элемент
преобразуется в элемент 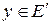 с помощью оператора
с помощью оператора 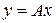 , элемент
, элемент 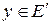 преобразуется в элемент
преобразуется в элемент 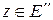 с помощью оператора
с помощью оператора 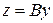 , то такое преобразование можно заменить одним преобразованием (оператором)
, то такое преобразование можно заменить одним преобразованием (оператором) 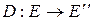 и записать
и записать
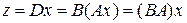 .
.
Оператор 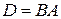 в этом случае называется суперпозицией операторов
в этом случае называется суперпозицией операторов 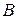 и
и 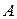 .
.
Если 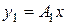 и
и 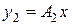 , где
, где 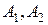 – операторы, действующие из
– операторы, действующие из 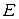 в
в 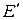 , то оператор
, то оператор 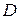 , действующий из
, действующий из 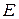 в
в 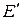 в соответствии с выражением
в соответствии с выражением
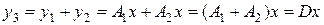 ,
,
называется суммой операторов 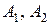 и обозначается
и обозначается 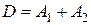 .
.
Если операторы 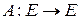 и
и 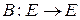 таковы, что
таковы, что
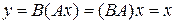 ,
,
то оператор 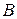 называется обратным к оператору
называется обратным к оператору 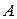 и обозначается
и обозначается 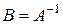 . В этих обозначениях предыдущее равенство приобретает вид
. В этих обозначениях предыдущее равенство приобретает вид
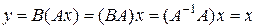 .
.
Оператор 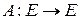 называется единичным, если
называется единичным, если 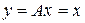 . Единичный оператор обозначается как
. Единичный оператор обозначается как 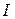 . В этих обозначениях мы имеем
. В этих обозначениях мы имеем 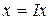 . Вполне понятно, что суперпозиция прямого и обратного оператора дает единичный оператор,
. Вполне понятно, что суперпозиция прямого и обратного оператора дает единичный оператор,
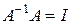 .
.
Оператор 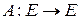 называется ограниченным, если существует такая постоянная величина
называется ограниченным, если существует такая постоянная величина 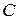 , что для всякого
, что для всякого 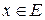
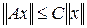 .
.
Наименьшее из чисел 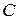 , удовлетворяющее этому неравенству, называется нормой оператора
, удовлетворяющее этому неравенству, называется нормой оператора 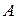 и обозначается
и обозначается 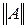 . Определенная таким образом норма
. Определенная таким образом норма 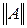 оператора
оператора 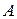 называется согласованной с нормой
называется согласованной с нормой 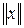 вектора
вектора 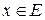 . Таким образом, согласованная норма оператора – это норма, подчиняющаяся условию
. Таким образом, согласованная норма оператора – это норма, подчиняющаяся условию
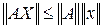
для 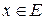 . Наиболее простой способ добиться согласованности нормы оператора с нормой вектора
. Наиболее простой способ добиться согласованности нормы оператора с нормой вектора 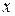 , уже введенной в
, уже введенной в 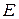 , – это принять определение
, – это принять определение
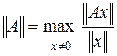 .
.
Такая норма называется операторной. Всякая операторная норма обладает свойством
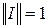 ,
,
где 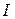 – единичный оператор. Норма оператора обладает следующими свойствами. Если операторы
– единичный оператор. Норма оператора обладает следующими свойствами. Если операторы 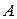 и
и 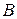 ограничены, то операторы
ограничены, то операторы 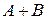 и
и 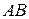 также ограничены, причем
также ограничены, причем
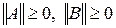 ,
,
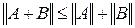 ,
,
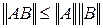 ,
,
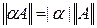 .
.
Функция 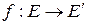 называется непрерывной в точке
называется непрерывной в точке 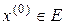 , если
, если 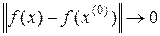 при
при 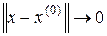 . Понятно, что пространства
. Понятно, что пространства 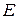 и
и 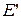 должны быть нормированными.
должны быть нормированными.
Функция 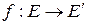 называется дифференцируемой в точке
называется дифференцируемой в точке 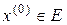 , если существует линейный оператор
, если существует линейный оператор 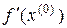 такой что
такой что
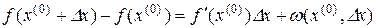 ,
,
где
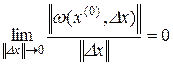 .
.
Указанный здесь оператор 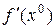 называется полной производной или производной Фреше функции
называется полной производной или производной Фреше функции 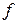 в точке
в точке 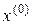 , а функция, имеющая производную Фреше, называется дифференцируемой по Фреше в точке
, а функция, имеющая производную Фреше, называется дифференцируемой по Фреше в точке 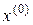 . Выражение
. Выражение 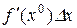 называется линейной частью приращения функции
называется линейной частью приращения функции 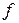 в точке
в точке 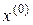 .
.
Итак, производная Фреше функции 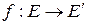 в точке
в точке 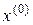 определена как линейный оператор,
определена как линейный оператор,
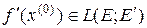 .
.
Если функция 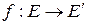 дифференцируема по Фреше во всех точках пространства
дифференцируема по Фреше во всех точках пространства 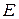 , то это означает, что каждому элементу
, то это означает, что каждому элементу 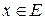 поставлен в соответствие линейный оператор, т.е. задана функция
поставлен в соответствие линейный оператор, т.е. задана функция
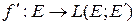 .
.
Аналогично определяются производные Фреше более высоких порядков. Так, производной Фреше второго порядка функции 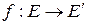 в точке
в точке 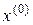 на-
на-
зывается линейный оператор 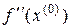 такой что
такой что
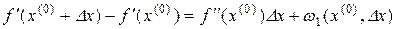 ,
,
где
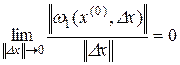 .
.
В соответствии с этим определением вторая производная Фреше в любой точке 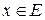 есть линейное отображение пространства
есть линейное отображение пространства 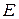 в пространство линейных операторов, действующих из
в пространство линейных операторов, действующих из 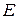 в
в 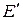 :
:
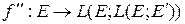 .
.
Приведем некоторые свойства производной Фреше.
1. Если 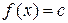 , где
, где 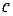 – константа, то
– константа, то 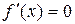 (производная константы).
(производная константы).
2. Если 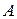 – линейный оператор, то
– линейный оператор, то 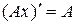 (производная линейного оператора).
(производная линейного оператора).
3. Если 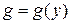 , где
, где 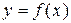 , т.е.
, т.е. 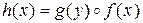 , то
, то 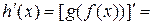

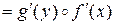 (производная сложной функции или суперпозиции функций).
(производная сложной функции или суперпозиции функций).
Формула Тейлора для отображения выражается, например, следующей теоремой из [27]: "пусть 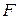 – отображение, действующее из
– отображение, действующее из 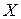 в
в 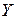 , определенное в некоторой области
, определенное в некоторой области 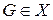 и такое, что
и такое, что 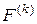 существует и представляет собой равномерно непрерывную функцию от
существует и представляет собой равномерно непрерывную функцию от 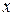 в
в  . Тогда имеет место равенство
. Тогда имеет место равенство
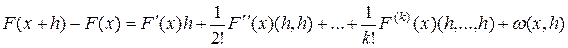 , (1.2.1)
, (1.2.1)
где
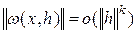 ",
", 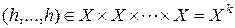 .
.
В приведенной теореме 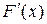 – производная Фреше,
– производная Фреше, 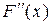 ,
, 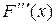 , – производные Фреше высших порядков.
, – производные Фреше высших порядков.
Формула (1.2.1) отличается краткостью и лаконичностью. Однако она имеет скорее теоретический, чем прикладной характер. Это связано с символичностью обозначений, которые не конкретизированы и в случае конечномерных пространств. Впрочем, в работе [27] отмечается, что в случае конечномерных евклидовых пространств 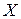 и
и 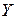 производная
производная 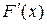 отображения
отображения 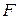 , действующего из
, действующего из 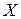 в
в 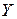 , есть зависящая от
, есть зависящая от 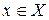
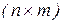 -матрица (
-матрица ( 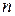 – размерность пространства
– размерность пространства 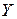 ,
, 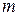 – размерность пространства
– размерность пространства 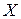 ). "Вторая производная
). "Вторая производная 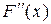 определяется в этом случае совокупностью
определяется в этом случае совокупностью 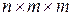 величин
величин 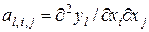 " [27]. Производные Фреше более высоких порядков в работе [27] не комментируются.
" [27]. Производные Фреше более высоких порядков в работе [27] не комментируются.
Как видно из приведенного обзора, функциональный анализ является весьма общим (обладающим теоретической общностью) и мощным, но и весьма абстрактным математическим аппаратом. Он приспособлен для теоретических исследований и совсем не приспособлен для практических расчетов. С точки зрения приведенных в разделах (1.1.2), (1.1.3) соображений этот подход следует считать плохо формализованным и вследствие этого не обладающим алгоритмической общностью.
Дата: 2019-02-02, просмотров: 511.