Подход функционального анализа характеризуется тем, что многомерные данные рассматриваются как элементы некоторых абстрактных математических пространств. При построении математических моделей данных используется понятие отображения этих пространств. Теоретической основой этого подхода является функциональный анализ [18, 25, 27, 77, 98, 103].
Математические пространства
Математическим пространством называется совокупность объектов (элементов), между которыми установлены определенные соотношения. Очевидно, что произвольное множество еще не математическое пространство, поскольку между его элементами не установлены какие-либо соотношения.
Пространство, элементами которого являются функции, называют функциональным пространством.
Непустое множество элементов 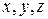 и т. д. называется линейным пространством, если в нем определены
и т. д. называется линейным пространством, если в нем определены
1) операция сложения элементов со свойствами
§ 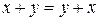 (коммутативность);
(коммутативность);
§ 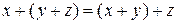 (ассоциативность);
(ассоциативность);
§ 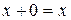 (существование нулевого элемента
(существование нулевого элемента 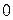 );
);
2) операция умножения элементов на любое число 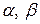 со свойствами
со свойствами
§ 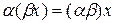 ;
;
§ 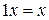 ;
;
§ 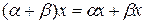 ;
;
§ 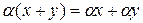 .
.
Приведем примеры линейных пространств.
Пример 1.7. Действительная прямая с известными операциями над действительными числами.
Пример 1.8. Пространство точек (векторов) 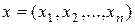 с известными правилами сложения векторов и умножения их на число.
с известными правилами сложения векторов и умножения их на число.
Пример 1.9. Пространство функций 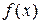 с веденными на нем операциями сложения функций и умножения их на число. Такое пространство называется линейным функциональным.
с веденными на нем операциями сложения функций и умножения их на число. Такое пространство называется линейным функциональным.
Отметим, что линейные пространства оказываются удобными для исследований, в связи с чем все известные и практически важные пространства оказываются линейными.
Множество 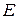 называется метрическим пространством, если для любых двух его элементов
называется метрическим пространством, если для любых двух его элементов 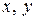 введена функция
введена функция 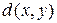 , которая называется расстоянием между
, которая называется расстоянием между 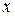 и
и 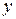 или метрикой, удовлетворяющая свойствам
или метрикой, удовлетворяющая свойствам
§  (симметричность);
(симметричность);
§ 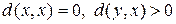 (неотрицательность);
(неотрицательность);
§ 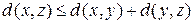 (неравенство треугольника).
(неравенство треугольника).
Пример 1.10. Действительная прямая с расстоянием между точками 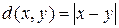 представляет собой метрическое пространство.
представляет собой метрическое пространство.
Пример 1.11. Пространство точек (векторов) 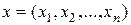 с расстоянием между двумя точками
с расстоянием между двумя точками 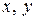 вида
вида
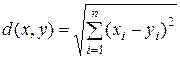
также является метрическим пространством.
Пример 1.12. Пространство функций 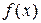 , интегрируемых на отрезке
, интегрируемых на отрезке 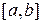 , с расстоянием между двумя функциями
, с расстоянием между двумя функциями 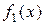 ,
, 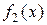 вида
вида
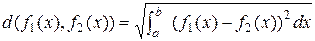 ,
,
является метрическим функциональным пространством.
Множество 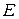 называется нормированным пространством, если для любого
называется нормированным пространством, если для любого 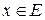 определена норма
определена норма 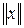 , обладающая свойствами
, обладающая свойствами
§ 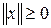 и
и 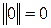 (неотрицательность);
(неотрицательность);
§ 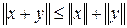 (выпуклость);
(выпуклость);
§ 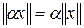 , где
, где 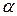 – число.
– число.
Норма 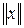 представляет собой не что иное, как длину вектора
представляет собой не что иное, как длину вектора 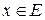 .
.
Если в пространстве введена норма, то в этом пространстве можно легко ввести метрику с помощью равенства
 .
.
С помощью этого соотношения любое нормированное пространство становится также и метрическим.
Пример 1.13. Действительная прямая 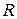 становится нормированным пространством, если для любого действительного числа
становится нормированным пространством, если для любого действительного числа 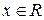 определить норму
определить норму 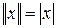 , где
, где 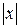 – модуль числа
– модуль числа 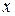 .
.
Пример 1.14. Если в 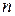 -мерном арифметическом пространстве
-мерном арифметическом пространстве 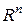 определить норму вектора
определить норму вектора 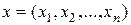 выражением
выражением
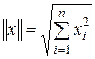 ,
,
то такое пространство становится нормированным. В этом пространстве можно теперь определить метрику с помощью выражения
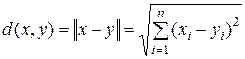
и тем самым превратить его в метрическое пространство.
Наиболее распространенным способом введения нормы в линейном пространстве 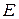 является введение в нем скалярного произведения двух элементов. Скалярным произведением двух элементов
является введение в нем скалярного произведения двух элементов. Скалярным произведением двух элементов 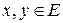 называется действительная функция, обозначаемая как
называется действительная функция, обозначаемая как 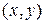 и обладающая свойствами
и обладающая свойствами
§ 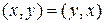 (симметричность);
(симметричность);
§ 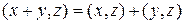 ;
;
§ 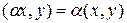 , где
, где 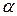 – число;
– число;
§ 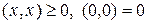 (неотрицательность).
(неотрицательность).
Пространство с введенным в нем скалярным произведением называется евклидовым пространством. В евклидовом пространстве легко ввести норму
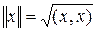 ,
,
сделав евклидово пространство нормированным. Можно также ввести метрику
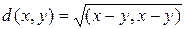 ,
,
сделав пространство метрическим.
Пример 1.15. Если в 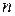 -мерном арифметическом пространстве
-мерном арифметическом пространстве 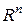 определить скалярное произведение двух векторов
определить скалярное произведение двух векторов 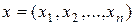 и
и 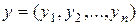 выражением
выражением
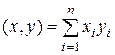 ,
,
то мы получим 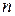 -мерное евклидово пространство. Норма в таком пространстве определяется выражением
-мерное евклидово пространство. Норма в таком пространстве определяется выражением
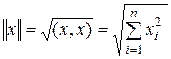 ,
,
а метрика (расстояние) – выражением
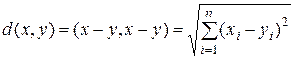 .
.
Такое расстояние, как известно, называется евклидовым. Евклидово 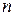 -мерное арифметическое пространство будем обозначать
-мерное арифметическое пространство будем обозначать 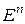 .
.
Дата: 2019-02-02, просмотров: 437.