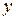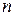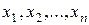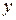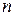Пусть теперь на показатель качества  некоторой системы влияет  факторов . Такую систему называют системой с одним выходом  и  входами  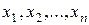и изображают так, как показано на рис 1.2.

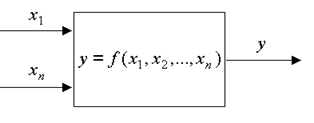
Рис. 1.2. Многомерная система

Это уже многомерная система, математической моделью которой может служить функциональная зависимость выходной переменной 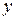 от входных переменных 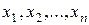. Модель данных классического подхода в этом случае представляет собой скалярную функцию многих переменных

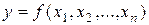.                                         (1.1.9)

Если модель линейна, то эта функция будет иметь вид

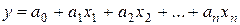.                              (1.1.10)

Квадратичная модель рассмотренной системы будет гораздо более громоздкой

по сравнению с линейной моделью (1.1.10),

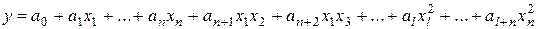. (1.1.11)

Важнейшим разделом классического анализа применительно к многомерным данным является дифференциальное исчисление функции многих переменных. Приведем основные свойства производных функции многих переменных.

1. Производная произведения. Правило дифференцирования не претерпевает существенных изменений по сравнению со скалярным случаем, за исключением того, что теперь рассматриваются частные производные. Итак, если 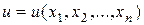, , 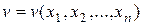то

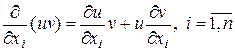.                          (1.1.12)

Пример 1.4. Пусть 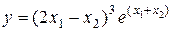, и требуется найти производную 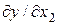. Введем функции 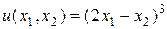, 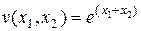. Тогда 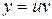, , 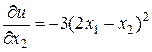, 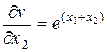и мы получим

.

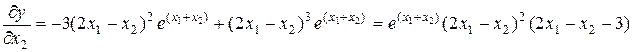2. Производная сложной функции. Если функции

,

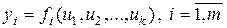зависят от промежуточных переменных 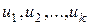, которые в свою очередь являются функциями независимых переменных 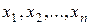, т.е.

,

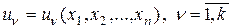то

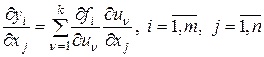.                    (1.1.13)

Более общим будет случай, когда дифференцируемые функции прямо зависят не только от промежуточных переменных , но и от независимых переменных 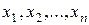. Итак, если

,

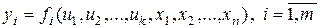где 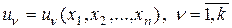, то

.                  (1.1.14)

Пример 1.5. Пусть

,

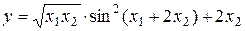и требуется найти производную 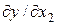. Введем промежуточные функции 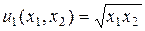, 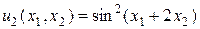. Тогда получим случай явной зависимости функции от промежуточных и независимых переменных:

.

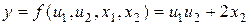В этом случае

.

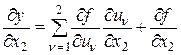Поскольку

, , , , ,

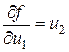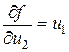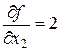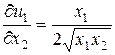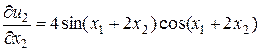то

.

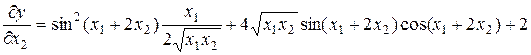3. Производная неявной функции. Если функции 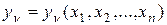, , 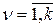заданы неявно в виде системы уравнений

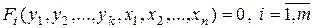,                     (1.1.15)

то производные 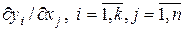, определяются как решение следующей системы линейных алгебраических уравнений:

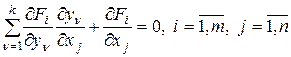.                     (1.1.16)

Пример 1.6. Пусть функция 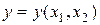 задана неявно с помощью уравнения

,

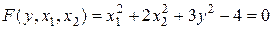 и требуется найти ее производные 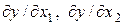. Это уравнение задает эллипсоид в трехмерном пространстве с координатами  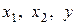с центром в точке 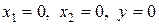. В этом случае нам необходимо составлять и решать следующую систему уравнений:

.

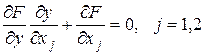Поскольку 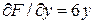, , 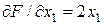, 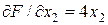то для определения искомых производных мы имеем следующую систему двух уравнений:

,

.

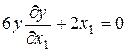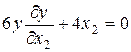Из этой системы получаем

, .

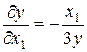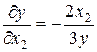Классический подход к записи формулы Тейлора для функции многих переменных 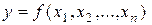 выражается, например, следующей теоремой из [32]: "если скалярная функция  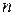переменных  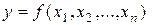определена и непрерывна вместе со всеми своими частными производными до порядка  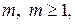включительно в некоторой 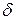-окрестности точки 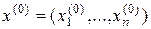, то справедлива формула

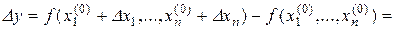
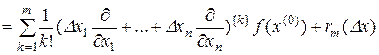,           (1.1.17)

где

".

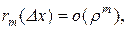
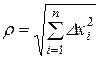В формуле (1.1.17) применена символическая запись

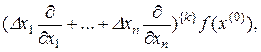                    (1.1.18)

которая, в частности, для двух переменных означает следующее:

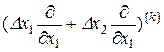
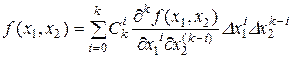.   (1.1.19)

Выполнение формулы (1.1.19) требует привлечения логического мышления (логических операций). Выражения, содержащие в явной или неявной форме логические операции, будем называть плохо формализованными. Программная реализация плохо формализованных выражений намного сложнее реализации хорошо формализованных выражений. Формулу (1.1.17) следует считать плохо формализованной из-за наличия в ней выражения вида (1.1.18). Кроме того, эта формула достаточна громоздка.

Еще один вариант записи формулы Тейлора для скалярной функции многих переменных, который также можно отнести к классическому, получается из (1.1.17) с помощью алгебраической формулы

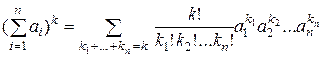
и имеет вид [32]

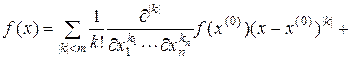
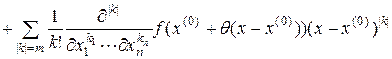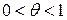, ,  (1.1.20)

где 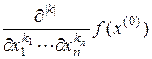 – смешанная производная 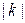-го порядка функции 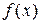, вычисленная в точке , , , , , , .

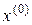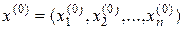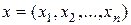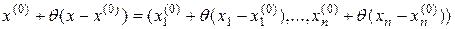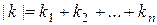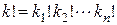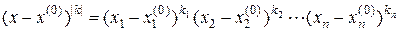Формула (1.1.20) также плохо формализована, так как при ее использовании приходится прибегать к логическим операциям. Например, необходимо просматривать все числа 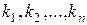. В выражении (1.1.20) вычисляется и добавляется новое слагаемое в том случае, если сумма чисел  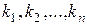равна 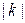. При рассмотрении векторной функции многих переменных формулы (1.1.17), (1.1.20) еще более усложнятся.

Выводы

Из приведенного краткого обзора просматриваются следующие недостатки классического подхода к анализу многомерных данных.

1. Громоздкость (необозримость) математических выражений. Это можно видеть на сравнении линейных моделей (1.1.2) и (1.1.10), квадратичных моделей (1.1.3) и (1.1.11), рядов и формул Тейлора (1.1.8) и (1.1.17).

2. Отсутствие аналогии со скалярным случаем. Действительно, многомерные модели (1.1.10), (1.1.11) нельзя назвать аналогичными скалярным моделям (1.1.2), (1.1.3). То же самое можно сказать и при сравнении выражений для ряда Тейлора (1.1.8) и формулы Тейлора (1.1.17). Иначе говоря, многомерные модели (1.1.10), (1.1.11), (1.1.17) не являются естественными обобщениями на многомерный случай скалярных моделей

 (1.1.2), (1.1.3), (1.1.8).

3. Плохая формализованность классического подхода, под которой будем понимать использование при определении моделей логических операций или логических представлений. Выражения, содержащие в явной или неявной форме логические операции, будем называть плохо формализованными. О плохой формализованности выражения обычно свидетельствует сопровождение его дополнительными словесными описаниями. Это существенно затрудняет понимание и особенно компьютерную реализацию выражения. Так, при записи квадратичной многомерной модели (1.1.11) нам пришлось воспользоваться многоточиями, смысл которых не совсем четко определен. Чтобы определить модель (1.1.11) вполне однозначно, необходимо условиться, каким образом упорядочиваются всевозможные произведения 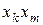. Можно сказать, что при использовании классического подхода к анализу многомерных данных возникает проблема упорядочивания. Эта проблема не разрешена в рамках классического подхода и должна решаться отдельно, что усложняет использование классического подхода в практических расчетах. Формула для многомерного ряда Тейлора (1.1.17) также плохо формализована, так как при ее использовании приходится прибегать к логическим операциям.

Важными характеристиками того или иного подхода являются возможность его реализации в виде алгоритма (компьютерной программы), а также теоретическая и алгоритмическая общность.

Под теоретической общностью будем понимать справедливость записанного выражения для любого числа переменных. Классический подход не обладает теоретической общностью. Действительно, выражение, задающее квадратичную модель системы для двух переменных, имеет вид

.

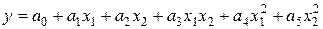Это выражение строго формализовано, однако оно не обладает теоретической общностью. Квадратичная модель для трех переменных задается совсем другим выражением

.

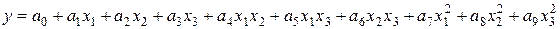Ситуация улучшается, если применить для квадратичной модели следующую запись

.

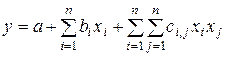Это выражение справедливо для любого числа переменных 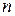, однако такая запись представляет собой переход к новому векторно-матричному подходу.

Под алгоритмической общностью будем понимать работоспособность алгоритма (или программы) для любого числа переменных без их модификации. Очевидно, что отсутствие теоретической общности влечет за собой отсутствие и алгоритмической общности. В связи с этим классический подход не обладает алгоритмической общностью. Вместе с тем теоретическая общность еще не обеспечивает алгоритмическую общность хотя бы потому, что выражение, обладающее теоретической общностью, может быть столь плохо формализованным, что не представляется возможным его реализация в виде алгоритма или программы.