Общие сведения
Сведения об электронном учебно-методическом комплексе по дисциплине «Анализ многомерных данных»
Электронный учебно-методический комплекс по дисциплине «Анализ многомерных данных» предназначен для студентов специальности 1-53 01 02 "Автоматизированные системы обработки информации".
Электронный учебно-методический комплекс разработан на основе учебной программы «Анализ многомерных данных», утверждённой ректором БГУИР 01 июля 2009 г., регистрационный № УД-53-116/уч.
Составитель:
В.С. Муха, заведующий кафедрой информационных технологий автоматизированных систем (ИТАС) Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники», доктор технических наук, профессор.
Рассмотрен и рекомендован к изданию на заседании кафедры ИТАС, протокол № 16 от 21.06.2011 г.
Одобрен и рекомендован к изданию методическим советом факультета информационных технологий и управления, протокол № 10 от 28.06.2011 г.
Методические рекомендации по изучению дисциплины
Виды занятий и формы контроля знаний определяются рабочей учебной программой дисциплины. Для студентов очной формы обучения предусмотрены лекции в объеме 32 часов, лабораторные работы в объеме 24 часов (6 четырехчасовых лабораторных работ) и экзамен по курсу.
Для студентов дистанционной формы обучения предусмотрена самостоятельная работа над теоретическим материалом дисциплины, две контрольные работы, два индивидуальных практических занятия и экзамен по курсу.
К сдаче экзамена студенты допускаются только при условии выполнения и защиты лабораторных работ (дневная форма обучения), выполнения и защиты контрольных работ и индивидуальных практических занятий (дистанционная форма обучения).
Последовательность изучения материала и выполнения индивидуальных практических занятий и контрольных работ студентами дистанционной формы обучения определяется рабочей учебной программой дисциплины.
Рабочая учебная программа
Учреждение образования
«Белорусский государственный университет
информатики и радиоэлектроники»
УТВЕРЖДАЮ
Декан факультета НИДО
______________ В.М. Бондарик
«______»_________ _______ г.
Регистрационный № УД-____________/р.
АНАЛИЗ МНОГОМЕРНЫХ ДАННЫХ
Рабочая учебная программа для специальности 1-53 01 02 Автоматизированные системы обработки информации
Факультет непрерывного и дистанционного обучения
Кафедра Информационных технологий автоматизированных систем
Курс 6-й
Индивидуальные практические Экзамен 6-й курс
занятия 2
Контрольные работы 2
Всего часов Форма получения
по дисциплине 136 высшего образования дистанционная
Минск 2011
Составил Муха В.С., д.т.н., профессор
Рабочая учебная программа составлена на основе учебной программы "Анализ многомерных данных", утвержденной ректором БГУИР 25.03.2011 г., рег. № УД-53-254/уч., и учебного плана специальности 1-53 01 02 «Автоматизированные системы обработки информации»
Рассмотрена и рекомендована к утверждению на заседании кафедры ИТАС протокол № ___ от «____»___________ г.
Заведующий кафедрой ____________(Муха В.С.)
Одобрена и рекомендована к утверждению Советом факультета ИТУ Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники»
протокол № ____ от «_____»________ _______ г.
Председатель ________________(Л.Ю. Шилин)
СОГЛАСОВАНО
Начальник ОМОУП______________Ц.С.Шикова
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цель преподавания дисциплины. Целью преподавания дисциплины является изложение студентам существующих подходов и методов обработки и анализа многомерных детерминированных и стохастических данных.
Задачи изучения дисциплины. Задачи изучения дисциплины состоят в обзоре существующих подходов к анализу многомерных данных, изложении нового многомерно-матричного подхода и рассмотрении задач, связанных с обработкой многомерных данных.
В результате освоения курса «Анализ многомерных данных» обучаемый должен:
Знать:
- существующие подходы к анализу многомерных данных;
- основные положения многомерно-матричного подхода к анализу многомерных данных;
уметь:
- выполнять математические операции с многомерными данными;
- выполнять программную реализацию методов анализа многомерных данных;
- выбирать программные средства в области анализа многомерных данных;
Иметь представление
- о практических задачах, связанных с анализом многомерных данных;
Перечень дисциплин, усвоение которых необходимо для изучения данной дисциплины.
| № | Название дисциплины | Раздел, тема |
| 1 | Высшая математика | Все разделы |
| 2 | Теории вероятностей и математическая статистика | Все разделы |
| 3 | Вычислительные методы и компьютерная алгебра | Все разделы |
| 4 | Статистические методы обработки данных | Все разделы |
Знания, полученные в рамках данной дисциплины, используются в дипломном проектировании и практической деятельности.
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
| Ку р с | Название и содержание тем (по типовой или учебной программе) | Контрольная работа (номер и тема по п.2) | Индивидуальная практическая работа (по п.1) | Оснащение контрольных, лабораторных и индивидуальных практических работ (по п.4) | Литература (по п.3) | Рекомендуемый объем для изучения (в часах) | Форма контроля знаний |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Раздел 1 Введение. Подходы к анализу многомерных данных | 1–3 | ||||||
| Тема 1. Классический подход к анализу многомерных данных. Понятие многомерных данных. Обзор существующих подходов к анализу многомерных данных. Характеристика классического подхода. | Тема 1. Представление данных рядами Тейлора: классический подход. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 8 | защита и.п.р. | ||
| Тема 2. Подход функционального анализа к анализу многомерных данных. Краткие сведения из функционального анализа и его характеристика | 1–3 | 9 | |||||
| Тема 3. Векторно-матричный и многомерно-матричный подходы к анализу многомерных данных. Характеристика векторно-матричного и многомерно-матричного подходов к анализу многомерных данных. | 1–3 | 8 | |||||
| Раздел 2 Основы многомерно-матричного подхода к анализу многомерных данных. | 1–3 | ||||||
| Тема 4. Определение и структура многомерной матрицы. Определение и структура многомерной матрицы. Транспонирование многомерной матрицы, симметричные многомерные матрицы. | 1–3 | 9 | |||||
Тема 5. Подстановки.
Подстановки на множестве индексов многомерной матрицы как биективные отображения. Суперпозиция подстановок. Некоторые типы подстановок. Операции над многомерными матрицами, ( 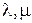 )-свернутое произведение многомерных матриц и его частные случаи. )-свернутое произведение многомерных матриц и его частные случаи.
| 1,4 | 8 | |||||
Тема 6. Формальные правила транспонирования многомерных матриц.
Формальные правила транспонирования многомерной матрицы. Повторное транспонирование многомерной матрицы. Транспонирование ( 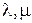 )-свернутого произведения многомерных матриц. )-свернутого произведения многомерных матриц.
| Тема 1. Многомерные матрицы. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 9 | защита к.р. | ||
| Тема 7. Многомерно-матричные полиномы. Многомерно-матричная форма представления полиномов произвольных степеней от многомерно-матричных аргументов. | Тема 2. Многомерно-матричные полиномы. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 8 | защита к.р. | ||
| Раздел 3 Линейные многомерно-матричные алгебраические уравнения. | 1–3 | ||||||
Тема 8. Единичные многомерные матрицы.
Единичные многомерные матрицы. Обратные многомерные матрицы. Матрицы, ( 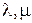 )-ассоциированные с многомерными матрицами. )-ассоциированные с многомерными матрицами.
| 1–3 | 9 | |||||
| Тема 9. Многомерно-матричные линейные алгебраические уравнения. Определитель многомерной матрицы. Многомерно-матричные линейные алгебраические уравнения. | 1–3 | 8 | |||||
| Тема 10. Дифференцирование по многомерно-матричному аргументу. Определение производной многомерно-матричной функции по многомерно-матричному аргументу (многомерно-матричной производной). Повторные производные по многомерно-матричному аргументу. Основные правила многомерно-матричного дифференцирования. | 1–3 | 9 | |||||
| Тема 11. Производные некоторых функций многомерно-матричного аргумента. Производные некоторых функций многомерно-матричного аргумента. Аппроксимация моделей многомерных данных рядами Тейлора. | Тема 2. Представление данных рядами Тейлора: многомерно-матричный подход. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 8 | защита и.п.р. | ||
| Раздел 5 Случайные векторы, матрицы и многомерные матрицы. | 1–3 | ||||||
| Тема 12. Определения и законы распределения случайного вектора, матрицы, многомерной матрицы. Определения случайного вектора, матрицы, многомерной матрицы, их законы распределения. Гауссовские векторы, матрицы, многомерные матрицы. | 1–3 | 9 | |||||
| Тема 13. Числовые характеристики случайных векторов, матриц, многомерных матриц. Числовые характеристики случайных векторов, матриц, многомерных матриц. Максимально-правдоподобные оценки гауссовских случайных матриц. Апостериорное распределение гауссовских случайных матриц. | 1–3 | 8 | |||||
| Тема 14. Определения и законы распределения векторного и матричного случайных процессов. Определение векторного и матричного случайного процесса, их законы распределения. Моментные функции векторного и матричного случайного процессов. Гауссовские матричные случайные процессы. Оценивание математических ожиданий и ковариационных функций векторных случайных процессов. | 1–3 | 9 | |||||
| Тема 15. Определение, законы распределения и моментные функции скалярного случайного поля. Определение скалярного случайного поля. Законы распределения и моментные функции скалярного случайного поля. Гауссовское случайное поле. Случайное поле, определенное на сетке значений аргументов. Аналогия описаний скалярного случайного поля на сетке значений аргументов и векторного случайного процесса. | 1–3 | 8 | |||||
| Раздел 7 Многомерная модель данных и OLAP-системы. | 1–3 | ||||||
| Тема 16. Реляционная и многомерная модели данных. Модели данных в системах управления базами данных (СУБД). OLAP-системы и 12 принципов Э. Кодда. Многомерная модель данных. Примеры многомерной модели данных | 9 | ||||||
| Итого | 2 | 2 | 136 | Экз. |
ЛИТЕРАТУРА
ОСНОВНАЯ
1. Муха В.С. Анализ многомерных данных. Монография. – Мн.: УП Технопринт, 2004. – 368 с.
2. Муха В.С., Корчиц К.С. Анализ многомерных данных: Лабораторный практикум. – Мн.: БГУИР, 2005. – 56 с.
3. Соколов Н.П. Введение в теорию многомерных матриц. – Киев: Наукова думка, 1972. – 175 с.
4. Калужнин Л.А., Сущанский В.И. Преобразования и перестановки. – М.: Наука, 1979. – 112 с.
ДОПОЛНИТЕЛЬНАЯ
5. Харин Ю.С., Степанова М.Д. Практикум на ЭВМ по математической статистике. – Мн.: Университетское, 1987. – 304 с.
6. Боровков А.А. Математическая статистика. Дополнительные главы. – М.: Наука, 1984. – 172 с.
7. Андерсон Т. Введение в многомерный статистический анализ. – М.: Физматгиз, 1963. – 500 с.
8. Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.
9. Уилкс С. Математическая статистика. – М.: Наука, 1967. – 632 с.
10. Дьяконов В.П., Абраменкова И.В. Матлаб 5.0/5.3. Система символьной математики. – М.: Нолидж, 1999. – 640 с.
11. Кетков Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 6.x: программирование численных методов. – СПб.: БХВ-Петербург, 2004. – 672 с.
АНАЛИЗ МНОГОМЕРНЫХ ДАННЫХ
Теоретический раздел
ВВЕДЕНИЕ
Предметом рассмотрения в данном пособии являются математические данные, т.е. данные, которые в языках программирования принято называть целыми или действительными константами или переменными.
Данные будем называть многомерными, если они состоят из одного или более чисел или одной или более переменных. При таком определении скалярные данные являются частным случаем многомерных, и на них распространяются все изложенные в данной работе результаты.
Под анализом данных будем понимать построение и исследование математических моделей данных, т.е. математических зависимостей, которые показывают, как данные преобразуются в различных физических процессах и системах.
Выводы
Из приведенного краткого обзора просматриваются следующие недостатки классического подхода к анализу многомерных данных.
1. Громоздкость (необозримость) математических выражений. Это можно видеть на сравнении линейных моделей (1.1.2) и (1.1.10), квадратичных моделей (1.1.3) и (1.1.11), рядов и формул Тейлора (1.1.8) и (1.1.17).
2. Отсутствие аналогии со скалярным случаем. Действительно, многомерные модели (1.1.10), (1.1.11) нельзя назвать аналогичными скалярным моделям (1.1.2), (1.1.3). То же самое можно сказать и при сравнении выражений для ряда Тейлора (1.1.8) и формулы Тейлора (1.1.17). Иначе говоря, многомерные модели (1.1.10), (1.1.11), (1.1.17) не являются естественными обобщениями на многомерный случай скалярных моделей
(1.1.2), (1.1.3), (1.1.8).
3. Плохая формализованность классического подхода, под которой будем понимать использование при определении моделей логических операций или логических представлений. Выражения, содержащие в явной или неявной форме логические операции, будем называть плохо формализованными. О плохой формализованности выражения обычно свидетельствует сопровождение его дополнительными словесными описаниями. Это существенно затрудняет понимание и особенно компьютерную реализацию выражения. Так, при записи квадратичной многомерной модели (1.1.11) нам пришлось воспользоваться многоточиями, смысл которых не совсем четко определен. Чтобы определить модель (1.1.11) вполне однозначно, необходимо условиться, каким образом упорядочиваются всевозможные произведения 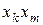 . Можно сказать, что при использовании классического подхода к анализу многомерных данных возникает проблема упорядочивания. Эта проблема не разрешена в рамках классического подхода и должна решаться отдельно, что усложняет использование классического подхода в практических расчетах. Формула для многомерного ряда Тейлора (1.1.17) также плохо формализована, так как при ее использовании приходится прибегать к логическим операциям.
. Можно сказать, что при использовании классического подхода к анализу многомерных данных возникает проблема упорядочивания. Эта проблема не разрешена в рамках классического подхода и должна решаться отдельно, что усложняет использование классического подхода в практических расчетах. Формула для многомерного ряда Тейлора (1.1.17) также плохо формализована, так как при ее использовании приходится прибегать к логическим операциям.
Важными характеристиками того или иного подхода являются возможность его реализации в виде алгоритма (компьютерной программы), а также теоретическая и алгоритмическая общность.
Под теоретической общностью будем понимать справедливость записанного выражения для любого числа переменных. Классический подход не обладает теоретической общностью. Действительно, выражение, задающее квадратичную модель системы для двух переменных, имеет вид
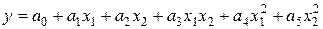 .
.
Это выражение строго формализовано, однако оно не обладает теоретической общностью. Квадратичная модель для трех переменных задается совсем другим выражением
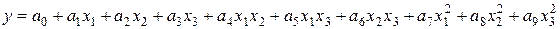 .
.
Ситуация улучшается, если применить для квадратичной модели следующую запись
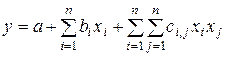 .
.
Это выражение справедливо для любого числа переменных 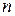 , однако такая запись представляет собой переход к новому векторно-матричному подходу.
, однако такая запись представляет собой переход к новому векторно-матричному подходу.
Под алгоритмической общностью будем понимать работоспособность алгоритма (или программы) для любого числа переменных без их модификации. Очевидно, что отсутствие теоретической общности влечет за собой отсутствие и алгоритмической общности. В связи с этим классический подход не обладает алгоритмической общностью. Вместе с тем теоретическая общность еще не обеспечивает алгоритмическую общность хотя бы потому, что выражение, обладающее теоретической общностью, может быть столь плохо формализованным, что не представляется возможным его реализация в виде алгоритма или программы.
Математические пространства
Математическим пространством называется совокупность объектов (элементов), между которыми установлены определенные соотношения. Очевидно, что произвольное множество еще не математическое пространство, поскольку между его элементами не установлены какие-либо соотношения.
Пространство, элементами которого являются функции, называют функциональным пространством.
Непустое множество элементов 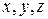 и т. д. называется линейным пространством, если в нем определены
и т. д. называется линейным пространством, если в нем определены
1) операция сложения элементов со свойствами
§ 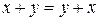 (коммутативность);
(коммутативность);
§ 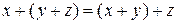 (ассоциативность);
(ассоциативность);
§ 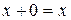 (существование нулевого элемента
(существование нулевого элемента 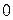 );
);
2) операция умножения элементов на любое число 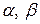 со свойствами
со свойствами
§ 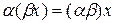 ;
;
§ 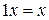 ;
;
§ 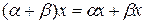 ;
;
§ 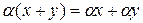 .
.
Приведем примеры линейных пространств.
Пример 1.7. Действительная прямая с известными операциями над действительными числами.
Пример 1.8. Пространство точек (векторов) 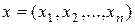 с известными правилами сложения векторов и умножения их на число.
с известными правилами сложения векторов и умножения их на число.
Пример 1.9. Пространство функций 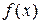 с веденными на нем операциями сложения функций и умножения их на число. Такое пространство называется линейным функциональным.
с веденными на нем операциями сложения функций и умножения их на число. Такое пространство называется линейным функциональным.
Отметим, что линейные пространства оказываются удобными для исследований, в связи с чем все известные и практически важные пространства оказываются линейными.
Множество 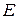 называется метрическим пространством, если для любых двух его элементов
называется метрическим пространством, если для любых двух его элементов 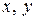 введена функция
введена функция 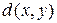 , которая называется расстоянием между
, которая называется расстоянием между 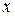 и
и 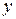 или метрикой, удовлетворяющая свойствам
или метрикой, удовлетворяющая свойствам
§  (симметричность);
(симметричность);
§ 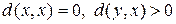 (неотрицательность);
(неотрицательность);
§ 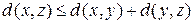 (неравенство треугольника).
(неравенство треугольника).
Пример 1.10. Действительная прямая с расстоянием между точками 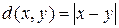 представляет собой метрическое пространство.
представляет собой метрическое пространство.
Пример 1.11. Пространство точек (векторов) 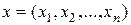 с расстоянием между двумя точками
с расстоянием между двумя точками 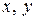 вида
вида
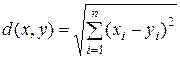
также является метрическим пространством.
Пример 1.12. Пространство функций 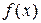 , интегрируемых на отрезке
, интегрируемых на отрезке 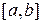 , с расстоянием между двумя функциями
, с расстоянием между двумя функциями 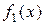 ,
, 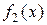 вида
вида
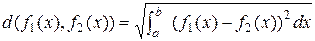 ,
,
является метрическим функциональным пространством.
Множество 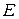 называется нормированным пространством, если для любого
называется нормированным пространством, если для любого 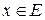 определена норма
определена норма 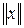 , обладающая свойствами
, обладающая свойствами
§ 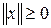 и
и 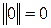 (неотрицательность);
(неотрицательность);
§ 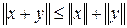 (выпуклость);
(выпуклость);
§ 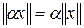 , где
, где 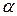 – число.
– число.
Норма 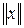 представляет собой не что иное, как длину вектора
представляет собой не что иное, как длину вектора 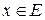 .
.
Если в пространстве введена норма, то в этом пространстве можно легко ввести метрику с помощью равенства
 .
.
С помощью этого соотношения любое нормированное пространство становится также и метрическим.
Пример 1.13. Действительная прямая 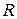 становится нормированным пространством, если для любого действительного числа
становится нормированным пространством, если для любого действительного числа 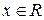 определить норму
определить норму 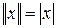 , где
, где 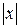 – модуль числа
– модуль числа 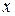 .
.
Пример 1.14. Если в 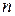 -мерном арифметическом пространстве
-мерном арифметическом пространстве 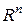 определить норму вектора
определить норму вектора 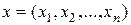 выражением
выражением
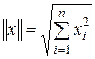 ,
,
то такое пространство становится нормированным. В этом пространстве можно теперь определить метрику с помощью выражения
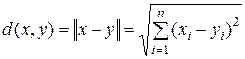
и тем самым превратить его в метрическое пространство.
Наиболее распространенным способом введения нормы в линейном пространстве 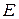 является введение в нем скалярного произведения двух элементов. Скалярным произведением двух элементов
является введение в нем скалярного произведения двух элементов. Скалярным произведением двух элементов 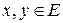 называется действительная функция, обозначаемая как
называется действительная функция, обозначаемая как 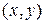 и обладающая свойствами
и обладающая свойствами
§ 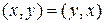 (симметричность);
(симметричность);
§ 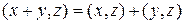 ;
;
§ 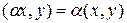 , где
, где 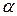 – число;
– число;
§ 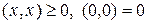 (неотрицательность).
(неотрицательность).
Пространство с введенным в нем скалярным произведением называется евклидовым пространством. В евклидовом пространстве легко ввести норму
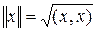 ,
,
сделав евклидово пространство нормированным. Можно также ввести метрику
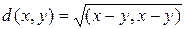 ,
,
сделав пространство метрическим.
Пример 1.15. Если в 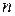 -мерном арифметическом пространстве
-мерном арифметическом пространстве 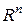 определить скалярное произведение двух векторов
определить скалярное произведение двух векторов 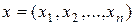 и
и 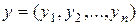 выражением
выражением
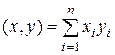 ,
,
то мы получим 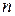 -мерное евклидово пространство. Норма в таком пространстве определяется выражением
-мерное евклидово пространство. Норма в таком пространстве определяется выражением
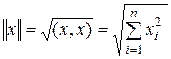 ,
,
а метрика (расстояние) – выражением
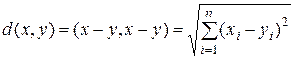 .
.
Такое расстояние, как известно, называется евклидовым. Евклидово 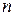 -мерное арифметическое пространство будем обозначать
-мерное арифметическое пространство будем обозначать 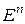 .
.
Основные понятия теории матриц
Матрицей размера 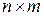 (двухмерной матрицей) называется набор чисел или
(двухмерной матрицей) называется набор чисел или
переменных, упорядоченных по строкам и столбцам в виде таблицы
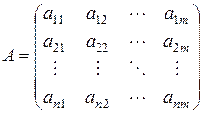 .
.
Коротко матрица обозначается как
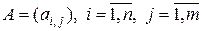 .
.
В общем случае 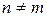 матрица называется прямоугольной, а при
матрица называется прямоугольной, а при 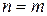 – квадратной или матрицей
– квадратной или матрицей 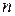 -го порядка. Матрица
-го порядка. Матрица
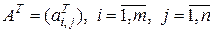 ,
,
элементы которой определяются по формуле
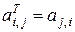 ,
,
называется транспонированной относительно 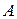 .
.
Матрица 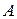 , совпадающая со своей транспонированной матрицей, т.е. удовлетворяющая равенству
, совпадающая со своей транспонированной матрицей, т.е. удовлетворяющая равенству 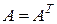 , называется симметричной.
, называется симметричной.
Матрицу, состоящую из одного столбца, называют вектором-столбцом,
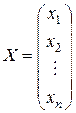 .
.
По определению принимается, что транспонированный вектор-столбец 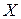 представляет собой вектор-строку,
представляет собой вектор-строку,

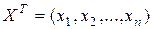 .
.
Для матриц определены операции умножения на число и сложения.
Суммой матриц 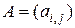 , и
, и 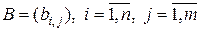 , называется матрица
, называется матрица 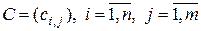 , элементы которой определяются формулой
, элементы которой определяются формулой
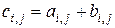 .
.
Сумма матриц обозначается как
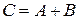 .
.
Произведением матрицы 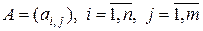 , на число
, на число 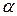 называется матрица
называется матрица 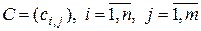 , элементы которой определяются формулой
, элементы которой определяются формулой
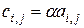 .
.
Произведение матрицы на число обозначается
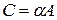 .
.
Матрица 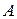 , все элементы которой равны нулю, называется нулевой и обозначается
, все элементы которой равны нулю, называется нулевой и обозначается 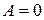 . Матрица
. Матрица 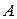
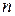 -го порядка, элементы которой определяются равенством
-го порядка, элементы которой определяются равенством
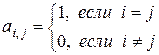 ,
,
называется единичной и обозначается 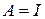 .
.
Рассмотрим пространство всевозможных 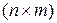 -матриц с введенными на нем вышеописанными операциями сложения и умножения на число. Легко видеть, что эти операции обладают следующими свойствами:
-матриц с введенными на нем вышеописанными операциями сложения и умножения на число. Легко видеть, что эти операции обладают следующими свойствами:
§ 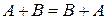 (коммутативность);
(коммутативность);
§ 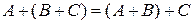 (ассоциативность);
(ассоциативность);
§ 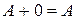 (существование нулевого элемента
(существование нулевого элемента 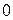 );
);
§ 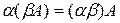 ;
;
§ 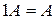 ;
;
§ 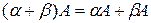 ;
;
§ 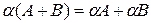 .
.
Отсюда мы видим, что множество прямоугольных матриц образует линейное
пространство.
Произведением 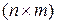 -матрицы
-матрицы 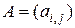 на
на  -матрицу
-матрицу 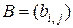 называется
называется 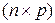 -матрица
-матрица 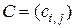 , элементы которой определяются как
, элементы которой определяются как
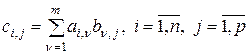 .
.
Произведение матриц обозначается
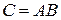 .
.
Частными случаями этого произведения являются скалярное и тензорное произведения векторов. Если 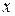 и
и 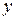 – векторы, содержащие по
– векторы, содержащие по 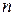 компонент, то произведение
компонент, то произведение
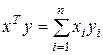
представляет собой число, называемое скалярным произведением 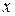 и
и 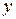 . Матрица
. Матрица 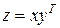 размера
размера 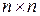 с элементами
с элементами 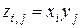 , называется тензорным произведением этих же векторов [29].
, называется тензорным произведением этих же векторов [29].
Для рассмотренных произведений справедливы следующие правила транспонирования:
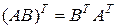 ,
,
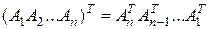 .
.
Известен еще один вид произведения матриц – кронекеровское произведение. В работе [30] это произведение называется прямым и определяется следующим образом. Прямое произведение 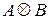 матрицы
матрицы 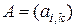 размера
размера 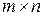 и матрицы
и матрицы 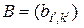 размера
размера 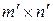 есть матрица
есть матрица
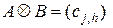 ,
, 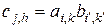 ,
,
размера 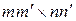 , где индекс
, где индекс 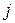 означает порядковый номер пары
означает порядковый номер пары 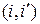 в последовательности
в последовательности 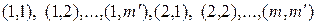 , а индекс
, а индекс  – порядковый номер пары
– порядковый номер пары 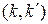 в аналогичной последовательности. В работе [7] приводится сдедующее лучше визуально воспринимаемое определение. Кронекеровское произведение
в аналогичной последовательности. В работе [7] приводится сдедующее лучше визуально воспринимаемое определение. Кронекеровское произведение 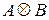 матрицы
матрицы 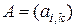 размера
размера 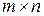 и матрицы
и матрицы 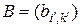 размера
размера 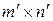 есть матрица размера
есть матрица размера 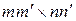 , определяемая формулой
, определяемая формулой
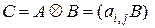 .
.
Пример 1.16. Если матрицы 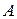 и
и 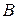 имеют вид
имеют вид
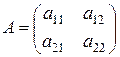 ,
, 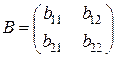 ,
,
то их кронекеровским произведением будет матрица
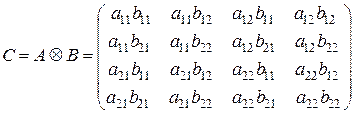 .
.
Для матрицы 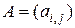
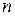 -го порядка определена скалярная функция, которая называется определителем матрицы и обозначается
-го порядка определена скалярная функция, которая называется определителем матрицы и обозначается 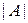 или
или 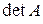 . Наиболее распространенный способ вычисления определителя матрицы
. Наиболее распространенный способ вычисления определителя матрицы 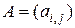 состоит в использовании его разложения по элементам
состоит в использовании его разложения по элементам 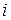 -й строки матрицы:
-й строки матрицы:
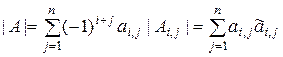 ,
,
где 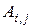 – матрица, которая получается после вычеркивания из исходной матрицы
– матрица, которая получается после вычеркивания из исходной матрицы 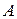
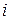 -й строки и
-й строки и 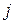 -го столбца. Числа
-го столбца. Числа 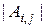 называются минорами матрицы
называются минорами матрицы 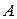 , а числа
, а числа 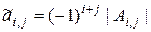 – алгебраическими дополнениями.
– алгебраическими дополнениями.
Для двух квадратных матриц 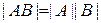 .
.
Матрица 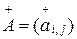
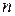 -го порядка называется присоединенной к матрице
-го порядка называется присоединенной к матрице 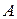
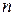 -го порядка, если она определяется выражением
-го порядка, если она определяется выражением
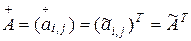 .
.
Матрица 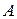
 -го порядка называется особенной, вырожденной или сингулярной, если
-го порядка называется особенной, вырожденной или сингулярной, если 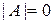 .
.
Для невырожденной матрицы 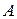
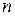 -го порядка существует обратная матрица
-го порядка существует обратная матрица
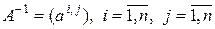 .
.
Это такая матрица, которая удовлетворяет равенству 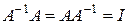 . Обратную матрицу можно получить по формуле
. Обратную матрицу можно получить по формуле
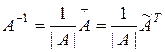 .
.
Справедлива следующая формула транспонирования обратной матрицы:
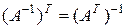 .
.
Если матрица разбита на отдельные матрицы (блоки), то она называется блочной. Практический интерес представляет формула Фробениуса для обращения блочной матрицы. Пусть 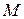 – невырожденная квадратная блочная матрица вида
– невырожденная квадратная блочная матрица вида
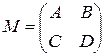 , (1.3.1)
, (1.3.1)
где 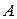 – квадратная невырожденная матрица (
– квадратная невырожденная матрица ( 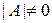 ). Тогда обратная матрица
). Тогда обратная матрица 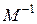 может быть определена по следующей формуле Фробениуса [12]
может быть определена по следующей формуле Фробениуса [12]
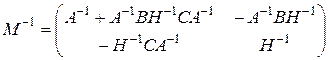 , (1.3.2)
, (1.3.2)
где
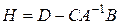 .
.
Если же предположить, что в матрице 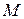 (1.3.1)
(1.3.1) 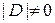 , то можно получить другой вид формулы Фробениуса
, то можно получить другой вид формулы Фробениуса
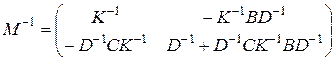 , (1.3.3)
, (1.3.3)
где
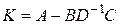 .
.
Прямоугольную матрицу 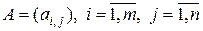 , можно рассматривать как оператор
, можно рассматривать как оператор 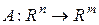 , действующий из
, действующий из 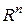 в
в 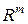 (см. раздел 1.2.2). В случае квадратной матрицы
(см. раздел 1.2.2). В случае квадратной матрицы 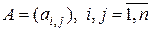 отображение
отображение
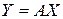
состоит в повороте вектора 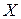 и изменении его длины (нормы). Ненулевые векторы
и изменении его длины (нормы). Ненулевые векторы 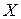 , для которых
, для которых
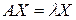 ,
,
называются собственными векторами матрицы 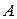 . Из определения собственных векторов ясно, что это такие векторы, которые отображаются матрицей
. Из определения собственных векторов ясно, что это такие векторы, которые отображаются матрицей 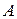 без поворота, а только с изменением их длины. Число
без поворота, а только с изменением их длины. Число 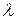 , соответствующее собственному вектору
, соответствующее собственному вектору 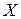 матрицы
матрицы 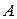 , называется собственным числом или собственным значением матрицы
, называется собственным числом или собственным значением матрицы 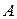 . Собственные векторы определяются как ненулевое решение однородного уравнения
. Собственные векторы определяются как ненулевое решение однородного уравнения
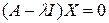 .
.
Такое решение существует, когда
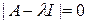 .
.
Собственные числа 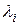 матрицы
матрицы 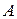 определяются как решение последнего уравнения.
определяются как решение последнего уравнения.
Как любой оператор, прямоугольная матрица 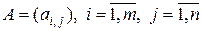 , может иметь норму (см. раздел 1.2.2). Эта норма должна быть согласованной с нормой вектора
, может иметь норму (см. раздел 1.2.2). Эта норма должна быть согласованной с нормой вектора  . С евклидовой нормой вектора
. С евклидовой нормой вектора 
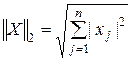
согласована спектральная норма матрицы
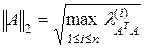 ,
,
где 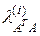 обозначены собственные числа матрицы
обозначены собственные числа матрицы 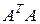 . Норма
. Норма 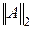 является операторной. С евклидовой нормой вектора согласована также евклидова норма матрицы
является операторной. С евклидовой нормой вектора согласована также евклидова норма матрицы
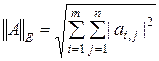 ,
,
которая, однако, не является операторной, поскольку для любой единичной матрицы 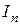
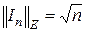 .
.
Векторно-матричный анализ
Если элементы матрицы 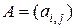 являются функциями скалярной переменной
являются функциями скалярной переменной 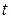 ,
, 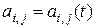 , то говорят, что матрица
, то говорят, что матрица 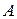 является функцией скалярного аргумента
является функцией скалярного аргумента 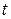 и записывают это в виде выражения
и записывают это в виде выражения 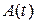 . Производная матричной функции скалярного аргумента определяется равенством
. Производная матричной функции скалярного аргумента определяется равенством
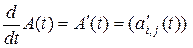 .
.
Аналогичным образом определяется интеграл от матричной функции скалярного аргумента:
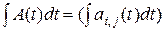 .
.
Таким образом, чтобы продифференцировать или проинтегрировать матричную функцию скалярного аргумента, необходимо продифференцировать или проинтегрировать по этому аргументу все ее элементы.
Более сложным является вопрос дифференцирования скалярной, векторной или матричной функции векторного или матричного аргумента. В работе [2] дается следующее определение производной скалярной функции матричного аргумента: если 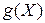 – скалярная функция матричного аргумента
– скалярная функция матричного аргумента 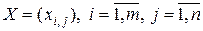 , то производной функции
, то производной функции 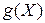 по
по 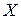 называется
называется 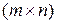 -матрица частных производных
-матрица частных производных
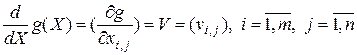 . (1.3.4)
. (1.3.4)
Эта производная в работе [2] названа скалярно-матричной. В соответствии с этим определением производная скалярной функции по вектору-строке является вектором-строкой частных производных, а по вектору-столбцу – вектором-столбцом частных производных.
Если 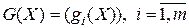 , – векторная функция векторного аргумента, то производная
, – векторная функция векторного аргумента, то производная  по
по 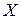 определяется как
определяется как 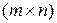 -матрица частных производных
-матрица частных производных
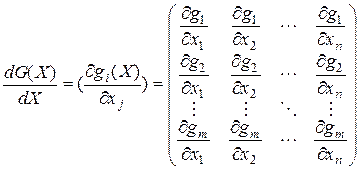 .
.
Эта матрица называется матрицей Якоби.
Практический интерес представляет дифференцирование линейных и квадратичных функций вектора-столбца 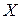 . Если в скалярной линейной функции
. Если в скалярной линейной функции
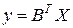
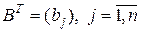 , – вектор-строка коэффициентов, то
, – вектор-строка коэффициентов, то
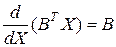 .
.
Если в векторной линейной функции
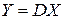
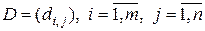 , – матрица коэффициентов, то
, – матрица коэффициентов, то
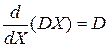 .
.
Для квадратичной формы вектора 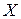
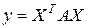
где 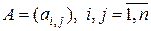 , – симметричная квадратная матрица коэффициентов, получены производные
, – симметричная квадратная матрица коэффициентов, получены производные
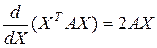 ,
,
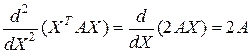 .
.
В работе [2] приведены некоторые скалярно-матричные производные (производные следа, определителя матрицы и др.). Эти производные получены также в разделах 3.2.13 – 3.2.15 данной работы в рамках аппарата многомерно-матричного дифференцирования.
Для дифференцирования матричной функции по матричному аргументу (матрично-матричное дифференцирование) в работе [2] введено понятие дифференциала матрицы: если 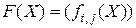 – матричная функция от матрицы
– матричная функция от матрицы 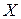 , то дифференциал
, то дифференциал 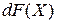 задается в виде
задается в виде
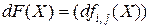 ,
,
где
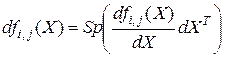 ,
,
и 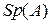 означает след матрицы
означает след матрицы 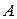 . Как видно, дифференциал матричной функции есть матрица тех же размеров, что и сама функция. Это позволяет авторам работы [2] при матрично-матричном дифференцировании не выходить за рамки обычных (двухмерных) матриц. В работе [2] получены дифференциалы некоторых матричных функций (произведения, степени, обратной матрицы и др.). Необходимо отметить, что нахождение дифференциала не всегда оказывается достаточным. Часто нужно иметь производную. В этом состоит ограничение подхода работы [2]. Кроме того, эта теория относится лишь к обычным (двухмерным) матрицам. Тем не менее этот подход находит в настоящее время применение. Так, некоторые скалярно-матричные производные приводятся в работах [19, 89].
. Как видно, дифференциал матричной функции есть матрица тех же размеров, что и сама функция. Это позволяет авторам работы [2] при матрично-матричном дифференцировании не выходить за рамки обычных (двухмерных) матриц. В работе [2] получены дифференциалы некоторых матричных функций (произведения, степени, обратной матрицы и др.). Необходимо отметить, что нахождение дифференциала не всегда оказывается достаточным. Часто нужно иметь производную. В этом состоит ограничение подхода работы [2]. Кроме того, эта теория относится лишь к обычным (двухмерным) матрицам. Тем не менее этот подход находит в настоящее время применение. Так, некоторые скалярно-матричные производные приводятся в работах [19, 89].
Теория скалярно-матричного дифференцирования позволяет записать три члена ряда Тейлора для скалярной функции 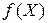 векторной переменной
векторной переменной 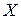 :
:
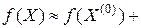
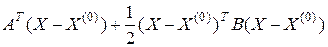 , (1.3.5)
, (1.3.5)
где 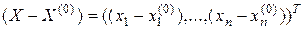 – вектор-столбец аргументов функции
– вектор-столбец аргументов функции 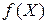 ,
, 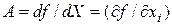 ,
, 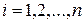 – первая производная функции
– первая производная функции 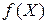 в точке
в точке 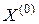 , которая называется градиентам функции
, которая называется градиентам функции 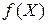 в точке
в точке 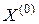 ,
, 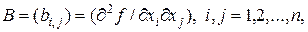 – вторая производная функции
– вторая производная функции 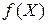 в точке
в точке 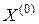 (
( 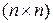 -матрица), которая называется матрицей Гессе в точке
-матрица), которая называется матрицей Гессе в точке 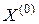 .
.
Записать последующие члены ряда Тейлора с помощью векторно-матричного подхода и теории скалярно-матричного дифференцирования не представляется возможным.
Выводы
Векторно-матричный подход преодолевает большинство недостатков классического подхода. Во-первых, он строго формализован и менее громоздок по сравнению с классическим подходом. Во-вторых, модели, полученные в рамках этого подхода, во многом аналогичны моделям скалярного случая. Поясним это на примере системы рис. 1.2. Если ввести в рассмотрение вектор-столбец входных воздействий 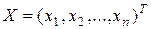 , то векторная модель (1.1.9) нашей системы запишется в виде
, то векторная модель (1.1.9) нашей системы запишется в виде
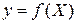 . (1.3.12)
. (1.3.12)
Линейная векторно-матричная модель (1.1.10) системы будет иметь вид
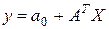 , (1.3.13)
, (1.3.13)
где 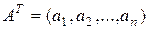 – матрица-строка коэффициентов модели. Квадратичная модель (1.1.11) запишется в виде
– матрица-строка коэффициентов модели. Квадратичная модель (1.1.11) запишется в виде
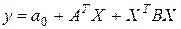 , (1.3.14)
, (1.3.14)
где 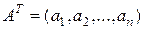 – матрица-строка коэффициентов при линейных членах модели, а
– матрица-строка коэффициентов при линейных членах модели, а 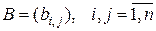 , – квадратная симметричная матрица коэффициентов при квадратичных членах. Мы видим, что выражения (1.3.13), (1.3.14) менее громоздки по сравнению с выражениями (1.1.10), (1.1.11). Кроме того, они аналогичны выражениям (1.1.2), (1.1.3) скалярного случая, т. е. являются их естественными обобщениями.
, – квадратная симметричная матрица коэффициентов при квадратичных членах. Мы видим, что выражения (1.3.13), (1.3.14) менее громоздки по сравнению с выражениями (1.1.10), (1.1.11). Кроме того, они аналогичны выражениям (1.1.2), (1.1.3) скалярного случая, т. е. являются их естественными обобщениями.
Однако векторно-матричный подход имеет и определенные недостатки. Он обладает ограниченными возможностями по представлению нелинейных данных, поскольку с его помощью можно получить не более чем квадратичные модели (1.3.14). Имеются случаи представления моделей третьей и даже четвертой степени [110], однако это скорее исключение, чем общее правило. В связи с этим считается, что матрицы являются “линейными преобразованиями” [7]. Понятие матрично-матричной производной определено лишь в форме дифференциала (раздел 1.3.1), что не всегда достаточно. Попытки использования для определения матрично-матричной производной кронекеровских произведений приводят к ухудшению формализованности подхода, поскольку кронекеровское произведение плохо формализовано. Кроме того, векторно-матричный подход не позволяет работать с многомерными массивами данных, широко применяемыми во всех языках программирования.
Имеются также попытки привлечения к анализу многомерных данных тензорного подхода, сводящегося к использованию тензора в качестве многомерной матрицы и операций внешнего и внутреннего произведения тензоров. Однако такой подход нельзя считать правомерным. Тензор определяется как геометрический объект в 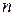 -мерном линейном пространстве
-мерном линейном пространстве 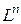 , в то время как многомерная матрица определяется как алгебраический объект в
, в то время как многомерная матрица определяется как алгебраический объект в 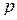 -мерном пространстве своих индексов. Это значит, что тензор не является многомерной матрицей. Общим свойством этих двух объектов является лишь то, что они представляют собой совокупности многоиндексных величин. Вместе с тем все индексы тензора пробегают значения от 1 до
-мерном пространстве своих индексов. Это значит, что тензор не является многомерной матрицей. Общим свойством этих двух объектов является лишь то, что они представляют собой совокупности многоиндексных величин. Вместе с тем все индексы тензора пробегают значения от 1 до 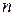 , в то время как индексы многомерной матрицы могут пробегать различное число значений. Это значит, что с использованием тензоров мы не получаем возможности работать с гиперпрямоугольными многомерными матрицами. Использование тензорных произведений также не дает никаких преимуществ, так как операции внешнего и внутреннего произведения тензоров не позволяют реализовать
, в то время как индексы многомерной матрицы могут пробегать различное число значений. Это значит, что с использованием тензоров мы не получаем возможности работать с гиперпрямоугольными многомерными матрицами. Использование тензорных произведений также не дает никаких преимуществ, так как операции внешнего и внутреннего произведения тензоров не позволяют реализовать 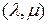 -свернутое произведение многомерных матриц при
-свернутое произведение многомерных матриц при 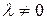 (см. раздел 2).
(см. раздел 2).
МНОГОМЕРНО-МАТРИЧНЫЙ АНАЛИЗ
В данном разделе анализируется состояние существующих подходов к теории матричного дифференцирования и разрабатывается теория многомерно-матричного дифференцирования.
Производная сложной функции
Пусть  – многомерно-матричная функция (
– многомерно-матричная функция ( 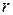 -мерная матрица)
-мерная матрица)
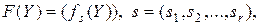
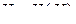 –
– 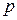 -мерная матрица,
-мерная матрица,

 –
–  -мерная матрица с различными (несовпадающими) элементами,
-мерная матрица с различными (несовпадающими) элементами,
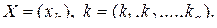
Тогда производная 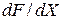 определяется как следующее
определяется как следующее 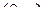 -свернутое произведение:
-свернутое произведение:
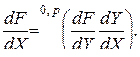 (3.2.4)
(3.2.4)
Докажем формулу (3.2.4). По определению (3.2.3) производная 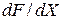 является
является 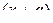 -мерной матрицей
-мерной матрицей
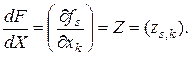
Так как для каждого элемента этой матрицы имеем формулу [30]
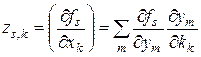 ,
,
то это означает справедливость формулы (3.2.4).
Более общим является случай функции 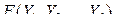 , где
, где 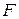 –
– 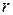 -мерная матрица,
-мерная матрица, 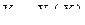 –
–  -мерные матрицы,
-мерные матрицы, 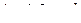 ,
,  –
–  -мерная матрица. Тогда
-мерная матрица. Тогда
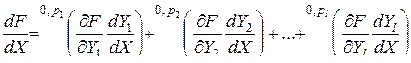 . (3.2.5)
. (3.2.5)
Эта формула следует из того, что для каждого элемента 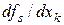 справедливо равенство [30]
справедливо равенство [30]
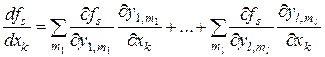 .
.
Если дифференцируемая сложная функция  ,
, 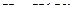 , явно зависит от аргумента
, явно зависит от аргумента  , т. е. имеет вид
, т. е. имеет вид  , то
, то
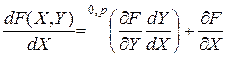 .
.
Эта формула вытекает из существующей для этого случая формулы дифференцирования для отдельного элемента матрицы 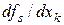 [30]
[30]
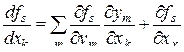 .
.
Производная произведения
Пусть 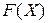 –
–  -мерная матрица,
-мерная матрица,
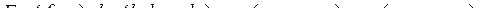
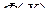 –
– 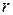 -мерная матрица,
-мерная матрица,
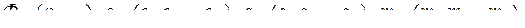
 –
–  -мерная матрица,
-мерная матрица,
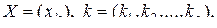
причем 
 ,
, 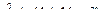 Справедлива следующая формула дифференцирования
Справедлива следующая формула дифференцирования 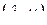 -свернутого произведения матриц
-свернутого произведения матриц 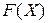 и
и 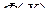 :
:
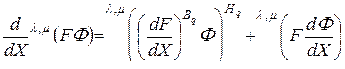 . (3.2.6)
. (3.2.6)
Здесь символами 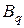 и
и 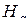 обозначены подстановки типа «вперед» и «назад» (2.8.11), (2.8.12) соответственно. Количество индексов подстановок
обозначены подстановки типа «вперед» и «назад» (2.8.11), (2.8.12) соответственно. Количество индексов подстановок 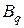 и
и 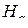 равно размерности транспонируемых матриц.
равно размерности транспонируемых матриц.
Для доказательства формулы (3.2.6) введем обозначения
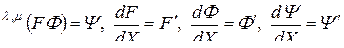 .
.
По определению 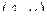 -свернутого произведения (2.2.17) для матриц
-свернутого произведения (2.2.17) для матриц 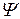 и
и  будем иметь выражения
будем иметь выражения
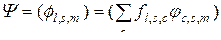 ,
,
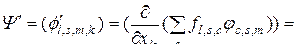
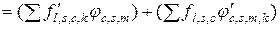 . (3.2.7)
. (3.2.7)
Второе слагаемое в правой части выражения (3.2.7) дает второе слагаемое в формуле (3.2.6), т.е.
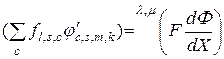 . (3.2.8)
. (3.2.8)
Первое слагаемое в правой части выражения (3.2.7) есть 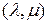 -свернутое произведение матриц
-свернутое произведение матриц 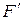 и
и 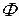 , однако свертывание производится не по внутренним индексам, как это принято в определении (2.2.17). Обозначим такое произведение как
, однако свертывание производится не по внутренним индексам, как это принято в определении (2.2.17). Обозначим такое произведение как  -свернутое,
-свернутое,
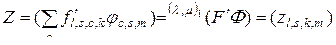 .
.
Выразим  -свернутое произведение через
-свернутое произведение через 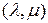 -свернутое произведение со свертыванием по внутренним индексам. Для этого введем матрицу
-свернутое произведение со свертыванием по внутренним индексам. Для этого введем матрицу
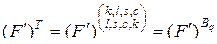 , (3.2.9)
, (3.2.9)
где символом 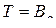 обозначена подстановка типа «вперед». Из формулы (3.2.9) следует, что
обозначена подстановка типа «вперед». Из формулы (3.2.9) следует, что
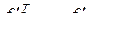 . (3.2.10)
. (3.2.10)
Найдем 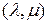 -свернутое произведение матриц
-свернутое произведение матриц 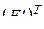 и
и 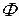
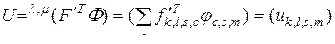 . (3.2.11)
. (3.2.11)
Подставив в формулу (3.2.11) выражение (3.2.10), получим
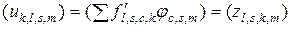 .
.
Из последнего равенства видно, что матрицы 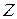 и
и 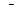 связаны соотношениями транспонирования
связаны соотношениями транспонирования
 ,
, 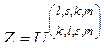 . (3.2.12)
. (3.2.12)
В результате первое слагаемое в выражении (3.2.7) приведено к виду
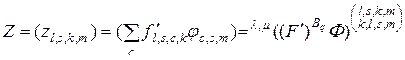 . (3.2.13)
. (3.2.13)
Однако порядок следования индексов в матрице (3.2.13) отличается от порядка следования индексов в производной  (3.2.7). Поэтому от матрицы Z необходимо перейти к матрице
(3.2.7). Поэтому от матрицы Z необходимо перейти к матрице 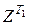 так, чтобы выполнялось условие
так, чтобы выполнялось условие
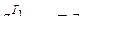 . (3.2.14)
. (3.2.14)
Подставляя выражение (3.2.12) в равенство (3.2.14), получаем
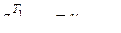 ,
,
или
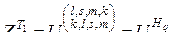 , (3.2.15)
, (3.2.15)
Учитывая формулу (3.2.11), запишем матрицу (3.2.15) в виде
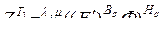 . (3.2.16)
. (3.2.16)
Теперь первое слагаемое в выражении (3.2.7) записано в форме (3.2.16), а второе слагаемое – в форме (3.2.8), что и доказывает формулу (3.2.6).
Производная неявной функции
Пусть функция 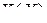 задана неявно равенством
задана неявно равенством
 , (3.2.17)
, (3.2.17)
где 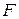 –
– 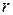 -мерная матрица,
-мерная матрица,
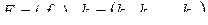 ,
,
 –
–  -мерная матрица,
-мерная матрица,
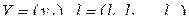 ,
,
 –
–  -мерная матрица,
-мерная матрица,
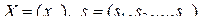 .
.
Тогда производная 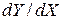 есть
есть 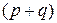 -мерная матрица, которая находится как решение следующего многомерно-матричного уравнения
-мерная матрица, которая находится как решение следующего многомерно-матричного уравнения
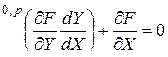 . (3.2.18)
. (3.2.18)
Действительно, расписав равенство (3.2.17) поэлементно,
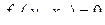 ,
, 

находим, что производные 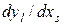 могут быть получены из системы линейных алгебраических уравнений [30]
могут быть получены из системы линейных алгебраических уравнений [30]
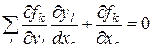 . (3.2.19)
. (3.2.19)
Система уравнений (3.2.19) в многомерно-матричной форме имеет вид (3.2.18).
Если функция 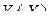 задана соотношением
задана соотношением
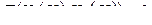 , (3.2.20)
, (3.2.20)
где 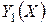 –
–  -мерная матрица,
-мерная матрица, 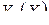 –
– 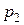 -мерная матрица,
-мерная матрица,  –
–  -мерная матрица, то
-мерная матрица, то  определяется как решение уравнения
определяется как решение уравнения
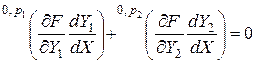 . (3.2.21)
. (3.2.21)
Это следует из правила (3.2.5).
Выводы
В разделе 3 выполнен анализ существующих подходов к двухмерно-матричному и многомерно-матричному дифференцированию и выявлены их ограничения и недостатки. Скалярно-матричное дифференцирование обладает теми ограничениями, что не выходит за рамки двухмерных матриц и, как следствие, не допускает повторного дифференцирования в форме производных, что приводит к трудностям в представлении функций рядами Тейлора, к неестественному определению дифференциала функции. Различные определения матрично-матричных производных также не выходят за рамки теории обычных (двухмерных) матриц. С этой целью в них используются кронекеровские произведения или векторные упорядочивания, что приводит к громоздкости и плохой формализованности таких производных. Известные результаты в области многомерно-матричного дифференцирования также громоздки, плохо формализованы, плохо согласуются с существующей теорией многомерных матриц, в связи с чем не получают дальнейшего развития. В разделе 3 разработана теория многомерно-матричного дифференцирования, свободная от указанных недостатков. В частности:
1) дано определение многомерно-матричной производной (3.2.3);
2) получены основные правила многомерно-матричного дифференцирования: дифференцирование сложной функции (3.2.4), (3.2.5), 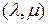 -свернутого произведения матриц (3.2.6), неявной функции (3.2.18), (3.2.21), транспонированной матрицы (3.2.22);
-свернутого произведения матриц (3.2.6), неявной функции (3.2.18), (3.2.21), транспонированной матрицы (3.2.22);
3) получены производные ряда многомерно-матричных функций: постоянной матрицы  по
по  (3.2.23), многомерной матрицы
(3.2.23), многомерной матрицы  по
по  (3.2.25), однородных многомерно-матричных полиномов 1-й степени (3.2.26), 2-й степени (3.2.30), (3.2.31),
(3.2.25), однородных многомерно-матричных полиномов 1-й степени (3.2.26), 2-й степени (3.2.30), (3.2.31), 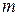 -й степени (3.2.38), (3.2.43)–(3.2.47),
-й степени (3.2.38), (3.2.43)–(3.2.47), 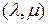 -обратной матрицы
-обратной матрицы 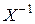 по
по  (3.2.48),
(3.2.48), 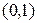 -обратной двухмерной матрицы
-обратной двухмерной матрицы 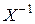 по
по  (3.2.50), определителя двухмерной матрицы
(3.2.50), определителя двухмерной матрицы  по
по  (3.2.51) и по
(3.2.51) и по 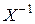 (3.2.52), логарифма определителя двухмерной матрицы
(3.2.52), логарифма определителя двухмерной матрицы  по
по  (3.2.56) и по
(3.2.56) и по 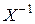 (3.2.57), евклидовой нормы многомерной матрицы
(3.2.57), евклидовой нормы многомерной матрицы  по
по  (3.2.58);
(3.2.58);
4) получено представление многомерно-матричной функции многомерно-матричным рядом Тейлора (3.2.61) и многомерно-матричная формула Тейлора (3.2.65);
5) дано определение полного дифференциала многомерно-матричной функции (3.2.66);
6) разработана теория дифференцирования функций симметричных двухмерных матриц (раздел 3.3), симметричных многомерных матриц (раздел 3.4), симметричных относительно множества мультииндексов многомерных матриц (раздел 3.5);
7) установлены соотношения между многомерно-матричным анализом и функциональным анализом (раздел 3.3).
СЛУЧАЙНЫЕ ПРОЦЕССЫ И ПОЛЯ
Скалярные случайные поля
Пусть задано некоторое вероятностное пространство 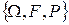 .
.
Определение. Скалярным случайным полем
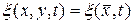 (10.4.1)
(10.4.1)
называется действительная скалярная функция 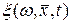 , которая для любых фиксированных аргументов
, которая для любых фиксированных аргументов 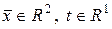 является измеримой функцией
является измеримой функцией 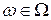 .
.
Аргумент 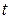 в этом определении понимается как время, а аргумент
в этом определении понимается как время, а аргумент 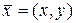 – как точка плоскости.
– как точка плоскости.
Если в трехмерном пространстве переменных 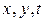 зафиксировать
зафиксировать  точек
точек
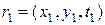 ,
, 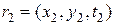 , …,
, …, 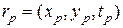 , (10.4.2)
, (10.4.2)
то получим  случайных величин – сечений случайного поля
случайных величин – сечений случайного поля
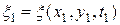 ,
, 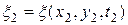 , … ,
, … , 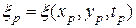 .
.
Распределение случайного вектора  при любом
при любом  и любых наборах точек
и любых наборах точек 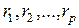 (10.4.2) назовем конечномерным (
(10.4.2) назовем конечномерным (  -мерным) распределением скалярного случайного поля.
-мерным) распределением скалярного случайного поля.
Определение. Конечномерной (  -мерной) функцией распределения скалярного случайного поля
-мерной) функцией распределения скалярного случайного поля  (10.4.1) назовем функцию распределения
(10.4.1) назовем функцию распределения  -мерного случайного вектора
-мерного случайного вектора  :
:
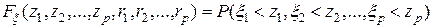 ,
,
где 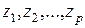 ,
, 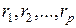 - аргументы функции распределения.
- аргументы функции распределения.
Определение. Конечномерной (  -мерной) плотностью вероятности скалярного случайного поля
-мерной) плотностью вероятности скалярного случайного поля  (10.4.1) называется функция
(10.4.1) называется функция
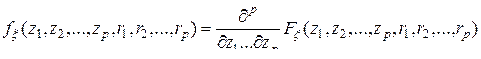
Замечание. Конечномерные (  -мерные) функция распределения и плотность вероятности случайного поля зависят от
-мерные) функция распределения и плотность вероятности случайного поля зависят от  точек плоскости
точек плоскости 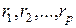 (10.4.2), на которых рассматриваются случайные величины
(10.4.2), на которых рассматриваются случайные величины 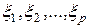 .
.
Определение. Математическим ожиданием случайного поля  (10.4.1) в точке
(10.4.1) в точке 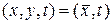 называется функция
называется функция 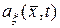 , определяемая выражением
, определяемая выражением
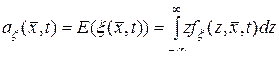 , (10.4.3)
, (10.4.3)
где 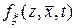 – одномерная плотность вероятности случайного поля.
– одномерная плотность вероятности случайного поля.
Определение. Дисперсией случайного поля  (10.4.1) в точке
(10.4.1) в точке 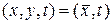 называется функция
называется функция 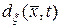 , определяемая выражением
, определяемая выражением
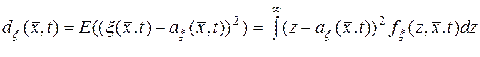 . (10.4.4)
. (10.4.4)
Определение. Ковариационной функцией случайного поля  (10.4.1) называется функция, определяемая выражением
(10.4.1) называется функция, определяемая выражением
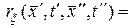
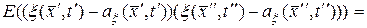
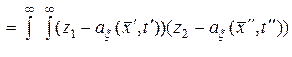
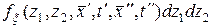 , (10.4.5)
, (10.4.5)
где 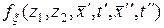 – двухмерная плотность вероятности случайного поля.
– двухмерная плотность вероятности случайного поля.
Ковариационная функция случайного поля обладает тем свойством, что
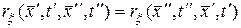 .
.
Дисперсия случайного поля может быть получена по его ковариационной функции,
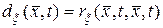 .
.
Определение. Конечномерным (  -мерным) математическим ожиданием случайного поля
-мерным) математическим ожиданием случайного поля  (10.4.1) на системе из
(10.4.1) на системе из  точек называется
точек называется  -мерный вектор
-мерный вектор 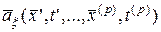 , являющийся математическим ожиданием вектора
, являющийся математическим ожиданием вектора  :
:
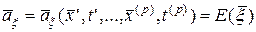 . (10.4.6)
. (10.4.6)
Определение. Ковариационной матрицей случайного поля  (10.4.1) на системе из
(10.4.1) на системе из  точек называется
точек называется 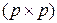 -матрица
-матрица 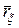 , которая является ковариационной матрицей вектора
, которая является ковариационной матрицей вектора  :
:
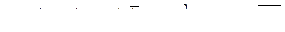 .
.
Элементы ковариационной матрицы могут быть получены по известной ковариационной функции с помощью формулы
 .
.
Определение. Случайное поле  (10.4.1) называется стационарным в узком смысле, если для любого
(10.4.1) называется стационарным в узком смысле, если для любого 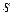
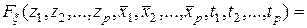
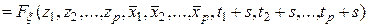 ,
,
где  –
–  -мерная функция распределения случайного поля.
-мерная функция распределения случайного поля.
Определение. Случайное поле  (10.4.1) называется стационарным в широком смысле, если его математическое ожидание не зависит от времени,
(10.4.1) называется стационарным в широком смысле, если его математическое ожидание не зависит от времени,
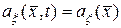 ,
,
а ковариационная функция зависит лишь от одного аргумента 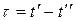 ,
,
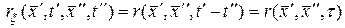 .
.
Ковариационная функция стационарного случайного поля обладает следующим
свойством:
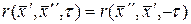 .
.
Определение. Случайное поле  (10.4.1) называется однородным в широком смысле, если для двух точек пространства аргументов
(10.4.1) называется однородным в широком смысле, если для двух точек пространства аргументов 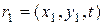 ,
, 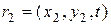 выполняются равенства
выполняются равенства
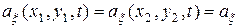 ,
,
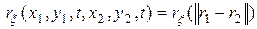 ,
,
где 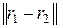 – расстояние между точками
– расстояние между точками 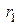 и
и 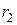 .
.
Определение. Случайное поле  (10.4.1) называется гауссовским, если все его конечномерные распределения гауссовские.
(10.4.1) называется гауссовским, если все его конечномерные распределения гауссовские.
Если случайное поле в момент времени 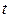 измеряется на сетке (матрице)
измеряется на сетке (матрице)  значений аргументов
значений аргументов 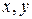 ,
,
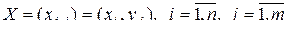 ,
,
то значения поля образуют двухмерную случайную матрицу
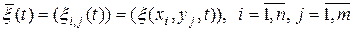 .
.
Математическим ожиданием случайного поля на сетке значений аргументов будет также двухмерная матрица
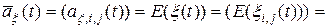
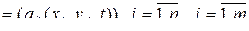 .
.
Ковариационная матрица случайного поля на сетке значений аргументов будет представлять собой четырехмерную 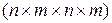 -матрицу
-матрицу
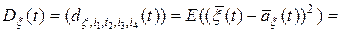
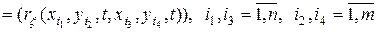 .
.
Плотность вероятности гауссовского случайного поля на сетке значений аргументов имеет вид
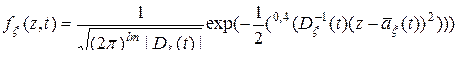 , (10.4.7)
, (10.4.7)
где 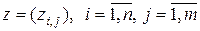 , – матричный аргумент плотности вероятности,
, – матричный аргумент плотности вероятности, 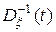 – матрица,
– матрица, 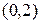 -обратная к
-обратная к 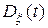 ,
, 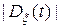 – определитель матрицы
– определитель матрицы 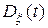 .
.
В практических приложениях чаще всего предполагается, что известна ковариационная функция случайного поля [122]. Часто используется ковариационная функция поля вида [17]
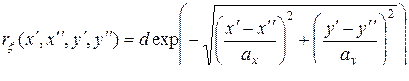 ,
,
где 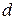 – дисперсия поля,
– дисперсия поля, 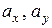 – параметры, характеризующие коррелированность поля в горизонтальном и вертикальном направлениях. В задачах фильтрации изображений иногда используется ковариационная функция вида [97]
– параметры, характеризующие коррелированность поля в горизонтальном и вертикальном направлениях. В задачах фильтрации изображений иногда используется ковариационная функция вида [97]
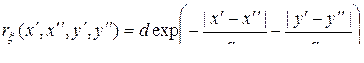 .
.
ЛИТЕРАТУРА
1. Альперович М. Введение в OLAP и многомерные базы данных. http://www.cfin.ru/itm/olap/intro.shtml?printversion
2. Амосов А.А., Колпаков В.В. Скалярно-матричное дифференцирование и его приложения к конструктивным задачам теории связи // Проблемы передачи информации. – 1972. – №. 8. – Вып. 1. – С. 3–15.
3. Аоки М. Оптимизация стохастических систем. – М.: Наука, 1971. – 424 с.
4. Баландин Ю.П., Милов Л.Т. Метод наименьших квадратов для многомерных массивов данных // Управление. Передача, преобразование и отображение информации / Межвузовский сб. статей. – Рязань, 1977. – Вып. 4. – С. 11–17.
5. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции: Гипергеометрическая функция, функция Лежандра. – М.: Наука, 1973. – 294 с.
6. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции: Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. – М.: Наука, 1974. – 295 с.
7. Беллман Р. Введение в теорию матриц. – М.: Наука, 1969. – 368 с.
8. Боровков А.А. Теория вероятностей. – М.: Наука, 1986. – 432 с.
9. Браммер К., Зиффлинг Г. Фильтр Калмана-Бьюси. – М.: Наука, 1982. – 200 с.
10.Гайшун И.В. Вполне разрешимые многомерные дифференциальные уравнения. – Мн.: Наука и техника, 1983. – 272 с.
11.Гайшун И.В. Линейные уравнения в полных производных. – Мн.: Наука и техника, 1989. – 254 с.
12.Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1988. – 552 с.
13.Гендель Е.Г., Мунерман В.И. Применение алгебраических моделей для синтеза процессов обработки файлов // Управляющие системы и машины. – 1984. – № 4. – С. 69–72.
14.Гурса Э. Курс математического анализа. – М.–Л.: ОНТИ, 1936. – Т. 1. –592 с.
15.Данилов Д.Л., Жиглявский А.А. Главные компоненты временных рядов: Метод "гусеница". – 1997.
16.Де Гроот М. Оптимальные статистические решения. – М.: Мир,1974. – 496 с.
17.Джайн А.К. Успехи в области математических моделей для обработки изображений // ТИИЭР. – 1981. – Т. 69. – № 5. – С. 9–39.
18.Дьедонне Ж. Основы современного анализа. – М.: Мир, 1964. – 432 с.
19.Ермаков С.М., Жиглявский А.А. Математическая теория оптимального эксперимента. – М.: Наука, 1987. – 320 с.
20.Икрамов Х.Д. Численные методы линейной алгебры. – М.: Знание, 1987. – 47 с.
21.Казаков И.Е. Обобщение метода статистической линеаризации на многомерные системы // Автоматика и телемеханика. – 1965. – Т. 26. – № 7. – С. 1210–1215.
22.Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.
23.Колло Д. Матричная производная для статистики. – Тарту: 1991. – 155 с.
24.Калужнин Л.А., Сущанский В.И. Преобразования и перестановки. – М.: Наука, 1979. – 112 с.
25.Картан А. Дифференциальное исчисление и дифференциальные формы. – М.: Мир, 1971. – 392 с.
26.Кендалл М., Стьюарт А. Теория распределений. – М.: Наука, 1966. – 587 с.
27.Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1972. – 496 с.
28.Колмогоров А.Н. Интерполирование и экстраполирование стационарных случайных последовательностей // Известия АН СССР. Сер. математическая. – 1941. – Т. 5.– С. 3–14.
29.Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: МЦНМО, 2001. – 960 с.
30.Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1973. – 832 с.
31.Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.
32.Кудрявцев Л.Д. Курс математического анализа. – М.: Высш. школа, 1981. – Т.2. – 584 с.
33.Левин Б.Р. Теоретические основы статистической радиотехники. Книга первая. – М.:Сов. радио, 1969. – 752 с.
34.Ли Р. Оптимальные оценки, определение характеристик и управление. – М.: Наука, 1966. – 176 с.
35.Лурье К.А. Оптимальное управление в задачах математической физики. – М.: Наука, 1975. – 478 с.
36.Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977. – 584 с.
37.Маркус М., Минк Х. Обзор по теории матриц и матричных неравенств. – М.: Наука, 1972. – 232 с.
38.Медич Дж. Статистически оптимальные линейные оценки и управление. – М.: Энергия, 1973. – 440 с.
39.Милов Л.Т. Многомерные матрицы при обработке массивов данных // Управление. Передача, преобразование и отображение информации / Межвузовский сб. статей. – Рязань, 1977. – Вып. 4. – С. 3–11.
40.Милов Л.Т. Многомерно-матричные производные и анализ чувствительности систем автоматического управления // Автоматика и телемеханика. – 1979. – № 9. – С. 15–25.
41.Митенков В.Б., Конычев В.И., Емельченко Е.П., Мунерман В.И., Самойлов М.Ю., Самойлова Т.А. // Эффективное решение задач обработки результатов летных испытаний на суперкомпьютерах // Тезисы докладов международной конференции "Авиационные технологии 2000". – Жуковский, 1997. – С. 15–16.
42.Монин А.С., Яглом А.М. Статистическая гидромеханика. Часть 1. – М.: Наука, 1965. – 639 с.
43.Мунерман В.И. Принципы создания многомерных аналитических информационных систем // Программа IV ежегодной научно-практической конференции "Создание единого информационного пространства Смоленской области" (25 апреля 2002 года) http://admin.smolensk.ru/sobyt/konfer/progr.htm
44.Мунерман В.И. Параллельная обработка данных. Методы и средства http://www.smolensk.ru/user/sgma/MMORPH/N-3-html/23.htm
45.Муха В.С. Нерекуррентный фильтр для гауссовских процессов // Автоматика и вычислительная техника. – 1985. – Вып.14. – C. 47–50.
46.Муха В.С. Многомерно-матричные производные и разложение функции нескольких переменных в ряд Тейлора // Автоматика и вычислительная техника. – 1987. – Вып. 16. – С. 65–71.
47.Муха В.С. Многомерно-матричные полиномы Эрмита // Известия АНБ. Сер. физ.-мат. наук. – 1990. – № 4. – С. 42–47.
48.Муха В.С. Многомерно-матричные дифференциальные уравнения и анализ чувствительности систем // Автоматика и вычислительная техника. – 1991. – Вып. 20. – С. 128–133.
49.Муха В.С. Многомерно-матричный подход к оцениванию реализаций векторных нестационарных процессов // Доклады 12 научно-технического семинара "Статистический синтез и анализ информационных систем" (23–25 июня 1992 г., г. Черкассы). – Москва-Черкассы, 1992. – С. 137–139.
50.Муха В.С. О многомерно-матричных дифференциальных уравнениях // Весцi АНБ. Сер. фiз.-мат. навук. – 1993. – № 2. – С. 37–44.
51.Муха В.С. Формальные правила транспонирования многомерных матриц // Автоматика и вычислительная техника. – 1993. – Вып. 21. – С. 65–72.
52.Муха В.С. К аппроксимации многомерных зависимостей и распределений рядами по полиномам Эрмита // Применение многомерного статистического анализа в экономике и оценке качества продукции: Тез. докл. 5-й науч. конф. стран СНГ. – М.: ЦЭМИ РАН, 1993. – С. 77–78.
53.Муха В.С. Ряды Фурье и Грама-Шарлье по многомерно-матричным полиномам Эрмита // Современные проблемы компьютерного анализа данных и моделирования: Сб. науч. ст. – Мн.: Белгосуниверситет, 1993. – С. 64–69.
54.Муха В.С. Расчет моментов многомерного гауссовского распределения // Весцi АНБ. Сер. фiз.-мат. навук. – 1993. – № 4. – С. 39–43.
55.Муха В.С. К теории полиномов Эрмита одной переменной и их применению // Автоматика и вычислительная техника. – Вып. 22.– Мн.,1994. – С. 58–63.
56.Муха В.С. Расчет моментов распределения Уишарта // Компьютерный анализ данных и моделирование: Сб. науч. ст. междунар. конф. (Минск, 4–8 сент. 1995 г.). – Т. 2. – Мн.: Белгосуниверситет, 1995. – С. 207–212.
57.Муха В.С. Дифференцирование функций симметричных матриц // Весцi АНБ. Сер. фiз.-мат. навук. – 1997. – № 2. – С. 46–53.
58.Муха В.С. К теории полиномов Лягерра векторной переменной // Еругинские чтения-IV: Тез. докл. междунар. матем. конф. (Витебск, 20–22 мая 1997 г.). – Витебск: Изд.-во Витебского госуниверситета, 1997. – С. 158–159.
59.Муха В.С. Многомерно-матричная технология для полиномов Лягерра векторной переменной в вероятностных приложениях // Электромагнитные волны и электронные системы. – 1998. – Т 3. – №4 . – С. 18–22.
60.Муха В.С. Многомерно-матричная технология в теории моделирования изображений // Материалы международной научно-технической конференции "Новые информационные технологии в науке и производстве".–Мн.:БГУИР,1998. – С. 199–202.
61.Муха В.С. Моделирование многомерных систем и процессов. Многомерно-матричный подход: Методическое пособие для аспирантов и научных работников. – Мн.: БГУИР, 1998. – 40 с.
62.Муха В.С. Многомерно-матричный подход к теории ортогональных систем полиномов векторной переменной // Тезисы докладов международной математической конференции "Еругинские чтения VI". (Гомель, 20–21 мая 1999 г.). – Часть 1. – Гомель: ГГУ им. Ф. Скорины, 1999. – C. 159–160.
63.Муха В.С. Байесовская фильтрация случайных полей и изображений // Вторая международная конференция "Цифровая обработка информации и управление в чрезвычайных ситуациях" (Минск, 28–30 ноября 2000 г.). Доклады. – Т. 1. – Мн., 2000. – С. 19 – 24.
64.Муха В.С. Многомерно-матричный подход к теории ортогональных систем полиномов векторной переменной // Весцi НАН Беларусi. Сер. фiз.-мат. навук.– 2001. – № 2. – С. 64–68.
65.Муха В.С. Статистическое распознавание многомерных негауссовских образов // Автоматика и телемеханика. – 2001. – № 4. – С. 80–90.
66.Муха В.С. Теория вероятностей: Учебное пособие для студентов технических специальностей высших учебных заведений. – Мн.: БГУИР, 2001. – 168 с.
67.Мысовских И.П. Интерполяционные кубатурные формулы. – М.: Наука, 1981. – 336 с.
68.Никифоров А.Ф., Уваров В.Б. Специальные функции математической физики. – М.: Наука, 1984. – 344 с.
69.Обухов А.М. Статистическое описание непрерывных полей // Труды геофизического института АН СССР. – 1954. – Вып. 24 (151). – С. 3–42.
70.Острем К.Ю. Введение в стохастическую теорию управления. – М.: Мир, 1973. – 322 с.
71.Принципы проектирования и использования многомерных баз данных (WinWord) http://students.informika.ru/essay/Detailed/1744.html
72.Прэтт У. Цифровая обработка изображений. – Кн. 1. – М.: Мир,1982. – 312 с.
73.Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Элементарные функции. – М.: Наука, 1981. – 800 с.
74.Пугачев В.С., Синицын И.Н. Стохастические дифференциальные системы. Анализ и фильтрация. – М.: Наука, 1990. – 632 с.
75.Рамм А.Г. Теория оценивания случайных полей. – М.: Мир, 1996. – 352 с.
76.Рао С.Р. Линейные статистические методы и их применение. – М.: 1968. – 548 с.
77.Рудин У. Основы математического анализа. – М.: Мир, 1976. – 319 с.
78.Сегё Г. Ортогональные многочлены. – М.: Физматгиз, 1962.
79.Синицын И.Н. Методы статистической линеаризации (обзор) // Автоматика и телемеханика. – 1974. – № 5. – С. 82–94.
80.Сираждинов С.Х. К теории многомерных полиномов Эрмита // Труды института математики и механики АН Уз. ССР. – 1949. – Вып. 5. – С. 70–95.
81.Соколов Н.П. Введение в теорию многомерных матриц. – Киев: Наукова думка, 1972. – 176 с.
82.Соколов Н.П. Пространственные матрицы и их приложения. – М.: Физматгиз, 1960. – 300 с.
83.Соколов Н.П. Об операциях над многомерными матрицами // Доклады АН СССР. – 1965. – Т. 163. – № 6. – С. 1322–1325.
84.Соколов Н.П. О функциях от многомерных матриц и применении их к решению линейных систем дифференциальных уравнений в частных производных // Укр. матем. журнал. – 1970. – Т. 22. – № 6. – С. 762–768.
85.Стрейц В. Методы пространства состояний в теории дискретных линейных систем управления. – М.: Наука, 1985. – 296 с.
86.Суетин П.К. Классические ортогональные многочлены. – М.: Наука, 1979. – 415 с.
87.Суетин П.К. Ортогональные многочлены по двум переменным. – М.: Наука, 1988. – 384 с.
88.Сю Д., Мейер А. Современная теория автоматического управления и ее применения. – М.: Машиностроение, 1972. – 552 с.
89.Тихонов В.И., Миронов М.А. Марковские процессы. – М.: Сов. радио, 1977. – 488 с.
90.Толстов Г.П. Курс математического анализа. – М.: Гос. изд. ТТЛ, 1957. – Т. 2. – 544 с.
91.Ту Ю. Современная теория управления. – М.:Машиностроение,1971. – 472 с.
92.Уилкс С. Математическая статистика. – М.: Наука, 1967. – 632 с.
93.Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. – М.-Л.: Физматгиз, 1963. – 734 с.
94.Феденя О.А. Многомерные матрицы и некоторые экстремальные комбинаторные задачи: Дис.-я на соиск. уч. ст. к. ф.-м. наук. – Ин-т матем. АН БССР. – 1978. – 103 с.
95.Фомин Я.А., Тарловский Г.Р. Статистическая теория распознавания образов. – М.: Радио и связь, 1986. – 264 с.
96.Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. – М.: Мир, 1980. – 280 с.
97.Хабиби А. Двумерная байесовская оценка изображений // ТИИЭР. – 1971. – Т. 60. – № 7. – С. 153–159.
98.Халмош П. Конечномерные векторные пространства. – М.:ФМ,1963. – 264 с.
99.Харин Ю.С. Робастность в статистическом распознавании образов. – Мн.: Университетское, 1985. – 232 с.
100. Харин Ю.С., Степанова М.Д. Практикум на ЭВМ по математической статистике. – Мн.: Университетское, 1987. – 304 с.
101. Хорн Р., Джонсон Ч. Матричный анализ. – М.: Мир, 1989. – 656 с.
102. Чукин Ю.В. Структуры данных для представления изображений // Зарубежная радиоэлектроника. – 1983. – № 8. – С. 87–103.
103. Шварц Л. Анализ. – Т . 1. – М.: Мир, 1972. – 824 с.
104. Шеффе Г. Дисперсионный анализ. – М.: Наука, 1980. – 512 с.
105. Шмелев А.Б. Основы марковской теории нелинейной обработки случайных полей. – М.: МФТИ, 1998. – 208 с.
106. Яншин В.В. Многосвязные цепи Маркова как пространственные матрицы // Доклады АН СССР. – 1991. – Т. 318. – № 5. – С. 1108–1112.
107. Appel P., Kampe de Feriet. Fonctions hypergeometriques et hyperspheriques. Polynomes D'Hermite. – Paris, 1926. – 390 p.
108. Bhatia R. Matrix Analysis. – Mew Dehli: Springer, 1997. – 347 p.
109. Brewer J.W. The derivative of the exponential matrix with respect to a matrix // IEEE Trans. – 1970. – V. AC-15. – № 2. – P. 241–244.
110. Brookes D.M. The Matrix Reference Manual. Section Matrix Calculus. – Imperial College of science, technology and medicine, London. http://www.cs.uwaterloo.ca/~frey/matrix/calculus.html
111. Dwyer P.S., Macphail M.S. Symbolic matrix derivatives // Annals of mathem. statistics. – 1948. – V. 19. – № 4. – P. 517–534.
112. Fraser R.A., Duncan W.Y., Collar A.R. Elementary matrices and some applications to dynamics and differential equations. – Cambridge university press, 1936.
113. Hermite M. Sur un nouveau doveloppement en serie des fonctions // Comptes Rendus hebdomadaires des seances de l'Academie des sciences. – 1864. – V. 58. – P. 93–100, 266–273.
114. Isserlis L. On a formula for the product-moment coefficient of any order of a normal frequency distribution in any number of variables // Biometrika. – 1918. – 12, № 1–2, – P. 134–139.
115. Kalman R.E. A new approach to linear filtering and prediction problems // Trans. ASME, series D. Journal of basic engineering. – March, 1960. – P. 35–45.
116. Krattenthaler C., Schlosser M. A new multidimensional matrix inverse with applications to multiple q-series // Discrete Mathematics. – 1999. – 204 . – P. 249–279.
117. MacRae E.C. Matrix derivatives with an application to adaptive linear decision problem // An. Statist. – 1974. – № 2. – P. 337–346.
118. Mukha V., Burtsev A. An Approach to the Multivariate Non-Gaussian Patterns Statistical Recognition // Computer Data Analysis and Modelling / Proceeding of the fifth Internationale Conference (Juni 8–12, 1998, Minsk, Republic of Belarus).– Minsk:BSU,1998. – P. 17–22.
119. Mukha V., Batin N. Statistical Recognition of Multivariate Essentially Non-Gaussian Patterns // Proceeding of Fifth International Conference PRIP'99 "Pattern Recognition and Information Processing" (May 18–20, 1999, Minsk, Republic of Belarus). – V. 1. – Minsk-Szczecin, 1999. – P. 163–167.
120. Mukha V.S. Statistical Recognition of Multivariate Non-Gaussian Patterns // Automation and Remote Control. – 2001. – V. 62. – № 4. – P. 580–590.
121. Neudecker H. Some theorems on matrix differentiations with special reference to Kronecker matrix products // J. Amer. Statist. Assoc. – 1969. – № 64. – P. 953–963.
122. Ramm A.G. Random Fields Estimation Theory. – New York: London Scientifik and Wiley, 1990.
123. Sebastiani P. On the Derivatives of Matrix Powers // SIAM Journal on Matrix Analysis and Applications. – V. 17(3). – July 1996. – P. 640–648.
124. Vetter W.J. Derivative operations on matrices // IEEE Trans. – 1970. – V. AC-15. – № 2. – P. 241–244.
Анализ многомерных данных
Практический раздел
Индивидуальные практические занятия для студентов специальности
1-53 01 02 "Автоматизированные системы обработки информации"
дистанционной формы обучения
Указания к выбору варианта
Выполните индивидуальные практические занятия по двум темам. Варианты возьмите из таблицы 1.0 в соответствии с последними двумя цифрами номера зачетки, отделенными дефисом. Если номер зачетки не содержит таких двух цифр, то обратитесь за вариантом к преподавателю. Отчет по каждой теме пришлите в виде отдельной папки, содержащей программы (m -файлы), отвечающие на каждый пункт "порядка выполнения работы". Имена файлов должны содержать номер пункта задания, например, файл с именем prog2_3_1.m решает задачи пункта 2.3.1 задания по теме 2. Если работа не зачтена, т.е. по ней имеются замечания, то присылайте работу целиком, включая и зачтенные вопросы (новую папку). Старая папка будет заменена новой и выполнена проверка.
Таблица 1.0
Номера вариантов индивидуальных практических занятий
| Две последние цифры зачетки | Вариант темы 1 по таблице 1.1 | Вариант темы 2 по таблице 1.2 |
| [ 1] | '1.03' | '2.18' |
| [ 2] | '1.30' | '2.05' |
| [ 3] | '1.13' | '2.11' |
| [ 4] | '1.19' | '2.07' |
| [ 5] | '1.01' | '2.12' |
| [ 6] | '1.16' | '2.03' |
| [ 7] | '1.21' | '2.02' |
| [ 8] | '1.08' | '2.03' |
| [ 9] | '1.25' | '2.09' |
| [ 10] | '1.02' | '2.25' |
| [ 11] | '1.22' | '2.14' |
| [ 12] | '1.03' | '2.23' |
| [ 13] | '1.25' | '2.22' |
| [ 14] | '1.27' | '2.01' |
| [ 15] | '1.21' | '2.26' |
| [ 16] | '1.28' | '2.08' |
| [ 17] | '1.04' | '2.20' |
| [ 18] | '1.26' | '2.27' |
| [ 19] | '1.08' | '2.18' |
| [ 20] | '1.26' | '2.03' |
| [ 21] | '1.29' | '2.08' |
| [ 22] | '1.17' | '2.30' |
| [ 23] | '1.26' | '2.18' |
| [ 24] | '1.01' | '2.08' |
| [ 25] | '1.22' | '2.25' |
| [ 26] | '1.19' | '2.19' |
| [ 27] | '1.11' | '2.16' |
| [ 28] | '1.27' | '2.21' |
| [ 29] | '1.01' | '2.27' |
| [ 30] | '1.21' | '2.04' |
| [ 31] | '1.17' | '2.01' |
| [ 32] | '1.17' | '2.15' |
| [ 33] | '1.13' | '2.05' |
| [ 34] | '1.18' | '2.02' |
| [ 35] | '1.29' | '2.04' |
| [ 36] | '1.19' | '2.24' |
| [ 37] | '1.02' | '2.20' |
| [ 38] | '1.22' | '2.20' |
| [ 39] | '1.10' | '2.10' |
| [ 40] | '1.04' | '2.26' |
| [ 41] | '1.19' | '2.09' |
| [ 42] | '1.16' | '2.23' |
| [ 43] | '1.03' | '2.09' |
| [ 44] | '1.10' | '2.29' |
| [ 45] | '1.11' | '2.29' |
| [ 46] | '1.21' | '2.12' |
| [ 47] | '1.22' | '2.21' |
| [ 48] | '1.16' | '2.01' |
| [ 49] | '1.26' | '2.26' |
| [ 50] | '1.26' | '2.22' |
| [ 51] | '1.08' | '2.01' |
| [ 52] | '1.08' | '2.29' |
| [ 53] | '1.03' | '2.19' |
| [ 54] | '1.29' | '2.06' |
| [ 55] | '1.11' | '2.21' |
| [ 56] | '1.13' | '2.13' |
| [ 57] | '1.03' | '2.26' |
| [ 58] | '1.22' | '2.13' |
| [ 59] | '1.30' | '2.21' |
| [ 60] | '1.29' | '2.20' |
| [ 61] | '1.26' | '2.10' |
| [ 62] | '1.11' | '2.29' |
| [ 63] | '1.11' | '2.21' |
| [ 64] | '1.02' | '2.22' |
| [ 65] | '1.27' | '2.26' |
| [ 66] | '1.19' | '2.16' |
| [ 67] | '1.01' | '2.15' |
| [ 68] | '1.04' | '2.02' |
| [ 69] | '1.11' | '2.1' |
| [ 70] | '1.30' | '2.25' |
| [ 71] | '1.23' | '2.03' |
| [ 72] | '1.22' | '2.01' |
| [ 73] | '1.03' | '2.18' |
| [ 74] | '1.12' | '2.13' |
| [ 75] | '1.02' | '2.07' |
| [ 76] | '1.02' | '2.09' |
| [ 77] | '1.05' | '2.01' |
| [ 78] | '1.18' | '2.24' |
| [ 79] | '1.10' | '2.17' |
| [ 80] | '1.19' | '2.15' |
| [ 81] | '1.25' | '2.03' |
| [ 82] | '1.17' | '2.01' |
| [ 83] | '1.30' | '2.10' |
| [ 84] | '1.29' | '2.20' |
| [ 85] | '1.11' | '2.13' |
| [ 86] | '1.17' | '2.09' |
| [ 87] | '1.23' | '2.24' |
| [ 88] | '1.30' | '2.20' |
| [ 89] | '1.13' | '2.11' |
| [ 90] | '1.13' | '2.13' |
| [ 91] | '1.10' | '2.26' |
| [ 92] | '1.09' | '2.21' |
| [ 93] | '1.03' | '2.30' |
| [ 94] | '1.13' | '2.12' |
| [ 95] | '1.10' | '2.14' |
| [ 96] | '1.12' | '2.17' |
| [ 97] | '1.24' | '2.18' |
| [ 98] | '1.18' | '2.25' |
| [ 99] | '1.29' | '2.21' |
Цель работы
1.1.1. Изучение аппроксимации функции одной переменной отрезками ряда Тейлора и исследование ее точности.
1.1.2. Изучение аппроксимации функции многих переменных отрезками ряда Тейлора с помощью классического подхода и исследование ее точности.
Теоретические положения
Порядок выполнения работы
1.3.1. Выбрать функцию из таблицы 1.1 в соответствии с номером своего варианта и получить (записать) для нее отрезок ряда Тейлора (1.1) в окрестности некоторой точки до 4-й степени независимой переменной включительно.
1.3.2. Написать m-файл-сценарий для аппроксимации функции одной переменной отрезками ряда Тейлора в окрестности некоторой точки от нулевой до 4-й степени независимой переменной включительно. C помощью программы plot вывести в одно графическое окно графики функции и аппроксимирующих полиномов. Проанализировать точность аппроксимации при различном числе слагаемых ряда Тейлора.
1.3.3. Выбрать функцию из таблицы 1.2 в соответствии с номером своего варианта, представив в ней скалярный аргумент 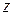 в виде полинома 1-й или 2-й степени переменных
в виде полинома 1-й или 2-й степени переменных  ,
, 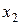 , например, в виде
, например, в виде
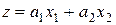 ,
,
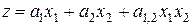 ,
,
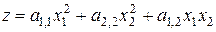 ,
,
и т.д. Для полученной таким образом функции двух переменных 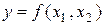 записать выражение ряда Тейлора (1.2) до 3-й степени независимых переменных включительно.
записать выражение ряда Тейлора (1.2) до 3-й степени независимых переменных включительно.
1.3.4. Написать m-файл-сценарий для аппроксимации функции двух переменных отрезками ряда Тейлора в окрестности некоторой точки от нулевой до 3-й степени независимой векторной переменной включительно. С помощью программы mesh вывести в одно графическое окно графики функции и аппроксимирующих полиномов. Проанализировать точность аппроксимации при различном числе слагаемых ряда Тейлора.
1.3.5. Оформить отчет, в котором привести функцию одной переменной, ее ряд Тейлора до 4-й степени независимой переменной включительно и графическую иллюстрацию аппроксимации, а также функцию двух переменных, ее ряд Тейлора до 3-й степени независимых переменных включительно и графическую иллюстрацию аппроксимации.
Таблица 1.1. Варианты заданий для функций одной переменной
| № вари-анта | Функция | № вари-анта | Функция |
| 1. | 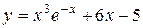
| 16. | 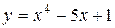
|
| 2. | 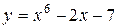
| 17. | 
|
| 3. | 
| 18. | 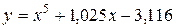
|
| 4. | 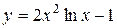
| 19. | 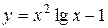
|
| 5. | 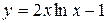
| 20. | 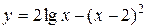
|
| 6. | 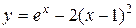
| 21. | 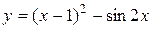
|
| 7. | 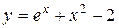
| 22. | 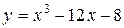
|
| 8. | 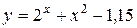
| 23. | 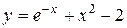
|
| 9. | 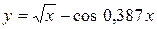
| 24. | 
|
| 10. | 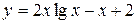
| 25. | 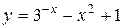
|
| 11. | 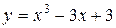
| 26. | 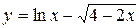
|
| 12. | 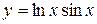
| 27. | 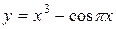
|
| 13. | 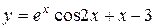
| 28. | 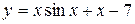
|
| 14. | 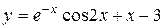
| 29. | 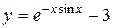
|
| 15. | 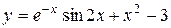
| 30. | 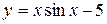
|
Таблица 1.2. Варианты заданий для функций двух переменных
| № вари-анта | Функция | № вари-анта | Функция |
| 1. | 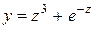
| 16. | 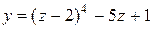
|
| 2. | 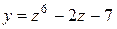
| 17. | 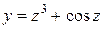
|
| 3. | 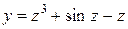
| 18. | 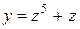
|
| 4. | 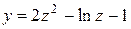
| 19. | 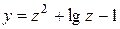
|
| 5. | 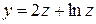
| 20. | 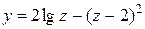
|
| 6. | 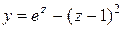
| 21. | 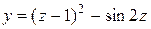
|
| 7. | 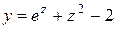
| 22. | 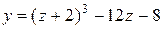
|
| 8. | 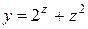
| 23. | 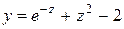
|
| 9. | 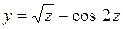
| 24. | 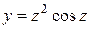
|
| 10. | 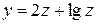
| 25. | 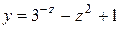
|
| 11. | 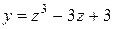
| 26. | 
|
| 12. | 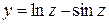
| 27. | 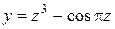
|
| 13. | 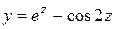
| 28. | 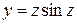
|
| 14. | 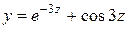
| 29. | 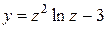
|
| 15. | 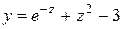
| 30. | 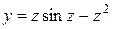
|
Цель работы
2.1.1. Изучение аппроксимации функции многих переменных отрезками ряда Тейлора с помощью многомерно-матричного подхода и исследование ее точности.
Теоретические положения
Пример
Приведем пример представления скалярной функции двух переменных многомерно-матричным рядом Тейлора. Рассмотрим функцию
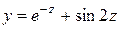 ,
,
где 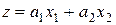 . В этом случае мы имеем скалярную функцию двух переменных
. В этом случае мы имеем скалярную функцию двух переменных 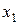 и
и 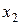 (одномерной матрицы второго порядка
(одномерной матрицы второго порядка 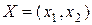 ). Если ввести одномерную матрицу коэффициентов
). Если ввести одномерную матрицу коэффициентов  , то
, то
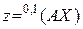 и
и 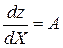 . Будем рассматривать разложение в ряд Тейлора в окрестности точки
. Будем рассматривать разложение в ряд Тейлора в окрестности точки 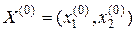 . Обозначим
. Обозначим
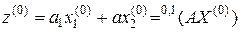 .
.
Тогда
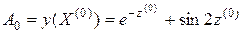 ,
,
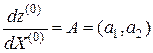 .
.
Заметим, что любая скалярная функция переменной 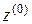 может перемещаться в многомерно-матричных произведениях в любое место как скалярная величина. Найдем коэффициенты
может перемещаться в многомерно-матричных произведениях в любое место как скалярная величина. Найдем коэффициенты 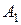 ,
, 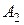 ,
, 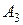 ,
, 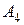 (2.2) ряда Тейлора (2.1). Получим
(2.2) ряда Тейлора (2.1). Получим
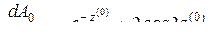 ,
,
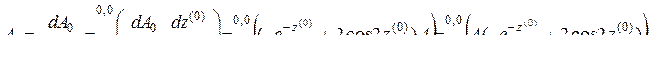 В последнем выражении мы изменили место функции
В последнем выражении мы изменили место функции  в произведении на основании сказанного выше. Этим приемом будем пользоваться и в дальнейшем. Далее, так как
в произведении на основании сказанного выше. Этим приемом будем пользоваться и в дальнейшем. Далее, так как 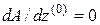 , то
, то
 ,
,
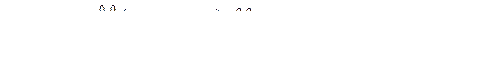
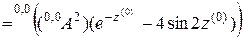 ,
,
где 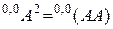 –
– 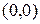 -свернутый квадрат матрицы
-свернутый квадрат матрицы  . Продолжим дифференцирование для поиска коэффициентов
. Продолжим дифференцирование для поиска коэффициентов 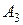 ,
, 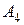 (2.2).
(2.2).
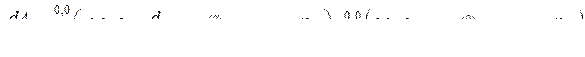
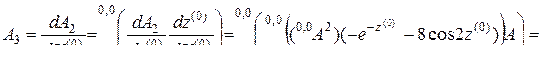
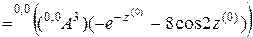 ,
,
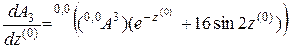 ,
,
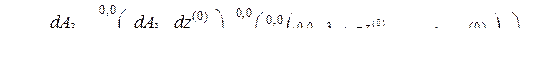
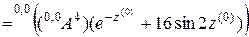 .
.
Отрезок ряда Тейлора для рассмотренной функции имеет вид
 .
.
Порядок выполнения работы
2.3.1. Выбрать функцию из таблицы 1.2 в соответствии с номером своего варианта, представив в ней скалярный аргумент 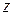 в виде полинома 1-й или 2-й степени переменных
в виде полинома 1-й или 2-й степени переменных  ,
, 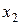 , например, в виде
, например, в виде 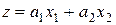 , или в виде
, или в виде
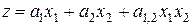 , (2.3)
, (2.3)
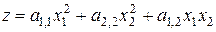 , (2.4)
, (2.4)
и т.д. Для полученной таким образом функции двух переменных 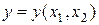 найти матрицы производных (2.2) до третьего порядка включительно. Воспользоваться при этом приведенными правилами многомерно-матричного дифференцирования [2, 3], оформив выбранную функцию
найти матрицы производных (2.2) до третьего порядка включительно. Воспользоваться при этом приведенными правилами многомерно-матричного дифференцирования [2, 3], оформив выбранную функцию 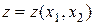 как промежуточную многомерно-матричную переменную. Например, для линейной функции
как промежуточную многомерно-матричную переменную. Например, для линейной функции 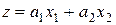 нужно ввести матрицы
нужно ввести матрицы  ,
, 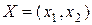 и записать ее в виде
и записать ее в виде 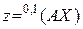 . Для квадратичных функций (2.3), (2.4) нужно дополнительно ввести симметричную матрицу коэффициентов
. Для квадратичных функций (2.3), (2.4) нужно дополнительно ввести симметричную матрицу коэффициентов
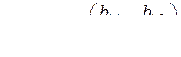 ,
, 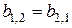 ,
,
и записать эти функции в виде 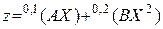 ,
, 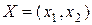 ,
, 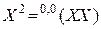 . При расчетах для получения функции (2.3) необходимо задать матрицу
. При расчетах для получения функции (2.3) необходимо задать матрицу 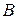 в виде
в виде
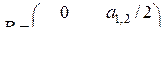 .
.
Для получения функции (2.4) матрицу  необходимо выбрать нулевой, а матрицу
необходимо выбрать нулевой, а матрицу 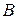 определить в виде
определить в виде
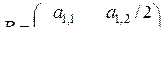 ,
,
т.е. записать функцию (2.4) в виде 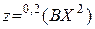 . С помощью варьирования значений матриц
. С помощью варьирования значений матриц  и
и  можно задавать другие функции двух переменных.
можно задавать другие функции двух переменных.
2.3.2. Написать m-файл-сценарий для аппроксимации данной функции двух переменных отрезками ряда Тейлора (2.1) в окрестности некоторой самостоятельно выбранной точки. В одно графическое окно с помощью программы mesh вывести графики функции и аппроксимирующих полиномов. Проанализировать точность аппроксимации при различном числе слагаемых ряда Тейлора.
2.3.3. Оформить отчет, в котором привести функцию двух переменных, ее многомерно-матричные производные и полученный отрезок ряда Тейлора.
ЛИТЕРАТУРА
1. Муха, В.С. Анализ многомерных данных: Монография / В.С. Муха. – Мн.: Технопринт, 2004. – 368 с.
2. Муха, В.С. Анализ многомерных данных: Лабораторный практикум / В.С. Муха. – Мн.: БГУИР, 2005. – 56 с.
3. Соколов, Н.П. Введение в теорию многомерных матриц / Н.П. Соколов. – Киев: Наукова думка, 1972. – 175 с.
4. Калюжнин, Л.А. Преобразования и перестановки / Л.А. Калюжнин, В.И. Сущанский. – М.: Наука, 1979. – 112 с.
5. Муха, В.С. Введение в MATLAB: Метод. пособие для выполнения лаб. работ по курсам "Статистические методы обработки данных" и "Теория автоматического управления" для спец. 53 01 02 "Автоматизированные системы обработки информации" / В.С. Муха, В.А. Птичкин. – Мн.: БГУИР, 2002. – 40 с.
6. Дьяконов, В.П. MATLAB 5.0/5.3. Система символьной математики / В.П. Дьяконов, И.В. Абраменкова. – М.: Нолидж. – 1999. – 740 с.
7. Муха, В.С. Теория вероятностей: Учеб. пособие для студентов технических специальностей высших учебных заведений / В.С. Муха. – Мн.: БГУИР, 2001. – 167 с.
Анализ многомерных данных
Контрольные работы для студентов специальности 1 53 01 02
"Автоматизированные системы обработки информации"
дистанционной формы обучения
Указания к выбору варианта
Выполните контрольные работы по двум темам. Варианты возьмите из таблицы 1.0 в соответствии с последними двумя цифрами номера зачетки, отделенными дефисом. Если номер зачетки не содержит таких двух цифр, то обратитесь за вариантом к преподавателю. Отчет по каждой теме пришлите в виде отдельной папки, содержащей программы (m -файлы), отвечающие на каждый пункт "порядка выполнения работы". Имена файлов должны содержать номер пункта задания, например, файл с именем prog2_3_1.m решает задачи пункта 2.3.1 задания по теме 2. Если работа не зачтена, т.е. по ней имеются замечания, то присылайте работу целиком, включая и зачтенные вопросы (новую папку). Старая папка будет заменена новой и выполнена проверка.
Таблица 1.0
Номера вариантов контрольных работ
| Последние две цифры зачетки | Вариант контрольной работы 1 по таблице 1.1 | Вариант контрольной работы 2 по таблице 2.1 |
| [ 1] | '1.29' | '2.07' |
| [ 2] | '1.19' | '2.15' |
| [ 3] | '1.27' | '2.23' |
| [ 4] | '1.14' | '2.01' |
| [ 5] | '1.25' | '2.14' |
| [ 6] | '1.19' | '2.24' |
| [ 7] | '1.28' | '2.23' |
| [ 8] | '1.06' | '2.13' |
| [ 9] | '1.29' | '2.28' |
| [ 10] | '1.13' | '2.27' |
| [ 11] | '1.02' | '2.11' |
| [ 12] | '1.25' | '2.01' |
| [ 13] | '1.05' | '2.07' |
| [ 14] | '1.06' | '2.19' |
| [ 15] | '1.09' | '2.06' |
| [ 16] | '1.01' | '2.23' |
| [ 17] | '1.14' | '2.28' |
| [ 18] | '1.15' | '2.13' |
| [ 19] | '1.26' | '2.16' |
| [ 20] | '1.07' | '2.21' |
| [ 21] | '1.26' | '2.01' |
| [ 22] | '1.21' | '2.12' |
| [ 23] | '1.25' | '2.16' |
| [ 24] | '1.22' | '2.13' |
| [ 25] | '1.10' | '2.06' |
| [ 26] | '1.06' | '2.21' |
| [ 27] | '1.10' | '2.17' |
| [ 28] | '1.05' | '2.21' |
| [ 29] | '1.12' | '2.26' |
| [ 30] | '1.26' | '2.18' |
| [ 31] | '1.15' | '2.27' |
| [ 32] | '1.25' | '2.20' |
| [ 33] | '1.25' | '2.20' |
| [ 34] | '1.21' | '2.09' |
| [ 35] | '1.11' | '2.17' |
| [ 36] | '1.22' | '2.10' |
| [ 37] | '1.26' | '2.18' |
| [ 38] | '1.12' | '2.22' |
| [ 39] | '1.17' | '2.14' |
| [ 40] | '1.21' | '2.19' |
| [ 41] | '1.24' | '2.29' |
| [ 42] | '1.16' | '2.27' |
| [ 43] | '1.06' | '2.30' |
| [ 44] | '1.09' | '2.08' |
| [ 45] | '1.27' | '2.23' |
| [ 46] | '1.05' | '2.01' |
| [ 47] | '1.27' | '2.06' |
| [ 48] | '1.09' | '2.20' |
| [ 49] | '1.09' | '2.15' |
| [ 50] | '1.02' | '2.30' |
| [ 51] | '1.18' | '2.13' |
| [ 52] | '1.16' | '2.11' |
| [ 53] | '1.13' | '2.07' |
| [ 54] | '1.18' | '2.23' |
| [ 55] | '1.16' | '2.20' |
| [ 56] | '1.07' | '2.12' |
| [ 57] | '1.24' | '2.21' |
| [ 58] | '1.14' | '2.18' |
| [ 59] | '1.25' | '2.22' |
| [ 60] | '1.19' | '2.02' |
| [ 61] | '1.13' | '2.10' |
| [ 62] | '1.27' | '2.01' |
| [ 63] | '1.24' | '2.30' |
| [ 64] | '1.30' | '2.24' |
| [ 65] | '1.14' | '2.15' |
| [ 66] | '1.07' | '2.20' |
| [ 67] | '1.10' | '2.29' |
| [ 68] | '1.22' | '2.13' |
| [ 69] | '1.23' | '2.09' |
| [ 70] | '1.14' | '2.29' |
| [ 71] | '1.21' | '2.07' |
| [ 72] | '1.26' | '2.19' |
| [ 73] | '1.05' | '2.07' |
| [ 74] | '1.19' | '2.19' |
| [ 75] | '1.12' | '2.18' |
| [ 76] | '1.14' | '2.02' |
| [ 77] | '1.01' | '2.10' |
| [ 78] | '1.11' | '2.12' |
| [ 79] | '1.21' | '2.03' |
| [ 80] | '1.02' | '2.19' |
| [ 81] | '1.19' | '2.01' |
| [ 82] | '1.01' | '2.06' |
| [ 83] | '1.18' | '2.02' |
| [ 84] | '1.12' | '2.19' |
| [ 85] | '1.22' | '2.21' |
| [ 86] | '1.03' | '2.14' |
| [ 87] | '1.14' | '2.11' |
| [ 88] | '1.05' | '2.21' |
| [ 89] | '1.21' | '2.22' |
| [ 90] | '1.15' | '2.17' |
| [ 91] | '1.04' | '2.14' |
| [ 92] | '1.22' | '2.27' |
| [ 93] | '1.09' | '2.08' |
| [ 94] | '1.26' | '2.07' |
| [ 95] | '1.25' | '2.28' |
| [ 96] | '1.07' | '2.08' |
| [ 97] | '1.02' | '2.03' |
| [ 98] | '1.20' | '2.16' |
| [ 99] | '1.26' | '2.06' |
Цель работы
1.1.1. Изучение основных положений теории многомерных матриц на основе системы Matlab.
Теоретические положения
Порядок выполнения работы
1.3.1. Сформировать 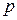 -мерную матрицу
-мерную матрицу 
 -го порядка и
-го порядка и 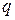 -мерную матрицу
-мерную матрицу 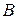
 -го порядка.
-го порядка.
1.3.2. Получить матрицу 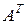 , транспонированную относительно
, транспонированную относительно  соответственно подстановке
соответственно подстановке 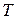 .
.
1.3.3. Получить матрицу 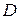 , равную
, равную 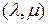 -свернутому произведению матриц
-свернутому произведению матриц  и
и 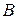 .
.
1.3.4. Сформировать 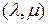 -единичную матрицу
-единичную матрицу 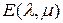
 -го порядка и найти произведение
-го порядка и найти произведение
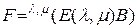 .
.
Указание. Необходимые параметры взять из табл. 1.1 в соответствии с номером варианта задания.
Таблица 1.1
| Номер варианта задания | Размер-ность  матри-цы матри-цы 
| Переста-новка 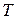
| Размер-ность 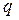 матри-цы матри-цы 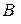
| Порядок 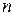 матриц матриц
 и и 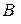
|
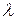
|

|
| 1. | 4 | 4,1,2,3 | 4 | 2 | 0 | 1 |
| 2. | 4 | 3,4,1,2 | 4 | 3 | 0 | 2 |
| 3. | 4 | 2,3,4,1 | 4 | 4 | 0 | 3 |
| 4. | 4 | 1,2,4,3 | 4 | 2 | 0 | 4 |
| 5. | 4 | 2,1,3,4 | 4 | 3 | 1 | 1 |
| 6. | 4 | 2,1,4,3 | 4 | 4 | 1 | 2 |
| 7. | 4 | 1,3,2,4 | 4 | 2 | 1 | 3 |
| 8. | 4 | 4,2,3,1 | 4 | 3 | 2 | 0 |
| 9. | 4 | 3,2,1,4 | 4 | 4 | 2 | 1 |
| 10. | 4 | 1,4,3,2 | 4 | 2 | 2 | 2 |
| 11. | 4 | 3,4,2,1 | 4 | 3 | 3 | 0 |
| 12. | 4 | 4,3,1,2 | 4 | 4 | 3 | 1 |
| 13. | 4 | 3,1,2,4 | 4 | 2 | 4 | 0 |
| 14. | 4 | 1,3,4,2 | 3 | 3 | 0 | 0 |
| 15. | 4 | 1,4,2,3 | 3 | 4 | 0 | 1 |
| 16. | 4 | 4,1,3,2 | 3 | 2 | 0 | 2 |
| 17. | 4 | 2,3,1,4 | 3 | 3 | 0 | 3 |
| 18. | 4 | 2,4,1,3 | 3 | 4 | 1 | 0 |
| 19. | 4 | 2,4,3,1 | 3 | 2 | 1 | 1 |
| 20. | 4 | 3,1,4,2 | 3 | 3 | 1 | 2 |
| 21. | 4 | 3,2,4,1 | 3 | 4 | 1 | 3 |
| 22. | 4 | 4,2,1,3 | 3 | 2 | 2 | 0 |
| 23. | 4 | 4,3,2,1 | 3 | 3 | 2 | 1 |
| 24. | 4 | 4,1,2,3 | 3 | 4 | 3 | 0 |
| 25. | 4 | 1,2,4,3 | 3 | 2 | 3 | 1 |
| 26. | 3 | 1,3,2 | 4 | 3 | 0 | 1 |
| 27. | 3 | 2,1,3 | 4 | 4 | 0 | 2 |
| 28. | 3 | 2,3,1 | 4 | 2 | 0 | 3 |
| 29. | 3 | 3,1,2 | 4 | 3 | 1 | 1 |
| 30 | 3 | 3,2,1 | 4 | 4 | 1 | 2 |
Цель работы
1. Изучение полиномов многих переменных на основе системы Matlab.
Теоретические положения
Порядок выполнения работы
2.3.1. Запрограммировать расчет скалярного полинома ( 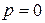 ) векторной переменной (
) векторной переменной ( 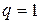 ) по выражениям (2.3) и (2.8) в случае двух переменных (
) по выражениям (2.3) и (2.8) в случае двух переменных ( 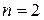 ). Варианты заданий приведены в табл. 2.1. Вывести в одно графическое окно трехмерный и контурный графики полинома (2.3), а в другое – трехмерный и контурный графики полинома (2.8) (с помощью функции meshc).
). Варианты заданий приведены в табл. 2.1. Вывести в одно графическое окно трехмерный и контурный графики полинома (2.3), а в другое – трехмерный и контурный графики полинома (2.8) (с помощью функции meshc).
Указание. Исходный полином задать в классическом представлении (2.3), выбрав коэффициенты 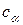 и степени
и степени 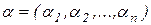 его переменных самостоятельно, а его многомерно-матричные коэффициенты в представлении (2.8) сформировать вручную путем сопоставления коэффициентов при одинаковых степенях переменных в классической и многомерно-матричной формах представления. Для такого сопоставления целесообразно записать эти две формы представления на бумаге. При правильном сопоставлении коэффициентов полинома двух форм представления (2.3) и (2.8) трехмерные графики в п. 2.3.1 должны совпадать. Для расчета значений полинома в многомерно-матричном представлении можно воспользоваться как непосредственно определением (2.8), так и схемой Горнера (2.13) (по выбору студента).
его переменных самостоятельно, а его многомерно-матричные коэффициенты в представлении (2.8) сформировать вручную путем сопоставления коэффициентов при одинаковых степенях переменных в классической и многомерно-матричной формах представления. Для такого сопоставления целесообразно записать эти две формы представления на бумаге. При правильном сопоставлении коэффициентов полинома двух форм представления (2.3) и (2.8) трехмерные графики в п. 2.3.1 должны совпадать. Для расчета значений полинома в многомерно-матричном представлении можно воспользоваться как непосредственно определением (2.8), так и схемой Горнера (2.13) (по выбору студента).
Таблица 2.1
| № варианта | Степень полинома 
| № варианта | Степень полинома 
| № варианта | Степень полинома 
|
| 1. | 3 | 11. | 3 | 21. | 3 |
| 2. | 2 | 12. | 4 | 22. | 2 |
| 3. | 3 | 13. | 3 | 23. | 3 |
| 4. | 4 | 14. | 2 | 24. | 4 |
| 5. | 5 | 15. | 3 | 25. | 3 |
| 6. | 2 | 16. | 4 | 26. | 2 |
| 7. | 3 | 17. | 3 | 27. | 3 |
| 8. | 4 | 18. | 2 | 28. | 4 |
| 9. | 3 | 19. | 3 | 29. | 3 |
| 10. | 2 | 20. | 4 | 30. | 5 |
ЛИТЕРАТУРА
1. Муха, В.С. Анализ многомерных данных: Монография / В.С. Муха. – Мн.: Технопринт, 2004. – 368 с.
2. Муха, В.С. Анализ многомерных данных: Лабораторный практикум / В.С. Муха, К.С. Корчиц. – Мн.: БГУИР, 2005. – 56 с.
3. Соколов, Н.П. Введение в теорию многомерных матриц / Н.П. Соколов. – Киев: Наукова думка, 1972. – 175 с.
4. Калюжнин, Л.А. Преобразования и перестановки / Л.А. Калюжнин, В.И. Сущанский. – М.: Наука, 1979. – 112 с.
5. Муха, В.С. Введение в MATLAB: Метод. пособие для выполнения лаб. работ по курсам "Статистические методы обработки данных" и "Теория автоматического управления" для спец. 53 01 02 "Автоматизированные системы обработки информации" / В.С. Муха, В.А. Птичкин. – Мн.: БГУИР, 2002. – 40 с.
6. Дьяконов, В.П. MATLAB 5.0/5.3. Система символьной математики / В.П. Дьяконов, И.В. Абраменкова. – М.: Нолидж. – 1999. – 740 с.
7. Муха, В.С. Теория вероятностей: Учеб. пособие для студентов технических специальностей высших учебных заведений / В.С. Муха. – Мн.: БГУИР, 2001. – 167 с.
КОНТРОЛЬ ЗНАНИЙ
Вопросы к экзамену по курсу "Анализ многомерных данных"
1. Классический подход к анализу данных: правила дифференцирования функции одной переменной, ряд Тейлора для функции одной переменной.
2. Классический подход к анализу многомерных данных: правила дифференцирования функций многих переменных.
3. Классический подход к анализу многомерных данных: ряд Тейлора для функции многих переменных.
4. Подход функционального анализа к анализу многомерных данных: линейное пространство, метрическое пространство, нормированное пространство, евклидово пространство.
5. Подход функционального анализа к анализу многомерных данных: операторы в линейных пространствах, линейный оператор, обратный оператор, сумма операторов, суперпозиция операторов.
6. Подход функционального анализа к анализу многомерных данных: непрерывный оператор, дифференцируемый оператор, производная Фреше, ряд Тейлора для дифференцируемого отображения.
7. Векторно-матричный подход к анализу многомерных данных: понятие матрицы и вектора, транспонирование матрицы, сложение, умножение матриц, умножение матрицы на число.
8. Векторно-матричный подход к анализу многомерных данных: определитель, след матрицы, обратная матрица, присоединенная матрица, транспонирование произведений матриц.
9. Векторно-матричный подход к анализу многомерных данных: дифференцирование, интегрирование матриц, зависящих от скалярного аргумента.
10. Векторно-матричный подход к анализу многомерных данных: дифференцирование скалярной функции по векторному и матричному аргументам, дифференцирование векторной функции по векторному аргументу.
11. Векторно-матричный подход к анализу многомерных данных: ряд Тейлора для функции векторной переменной.
12. Определение многомерной матрицы, симметричные многомерные матрицы.
13. Операции над многомерными матрицами (сложение, умножение на число, ( 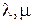 )-свернутое умножение).
)-свернутое умножение).
14. Частные случаи умножения многомерных матриц.
15. Многомерные единичные матрицы.
16. Матрицы, ассоциированные с многомерными матрицами. Теорема о произведении ассоциированных матриц.
17. Многомерные обратные матрицы.
18. Многомерно-матричные системы линейных алгебраических уравнений.
19. Подстановки (перестановки): определение, суперпозиция подстановок, тождественная, обратная подстановки, подстановки типа "вперед", "назад", "вперед-назад".
20. Транспонирование многомерных матриц: определение транспонированной матрицы, повторное транспонирование матрицы.
21. Транспонирование ( 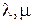 )-свернутого произведения многомерных матриц.
)-свернутого произведения многомерных матриц.
22. Определение многомерно-матричной производной, основные правила дифференцирования.
23. Производные некоторых многомерно-матричных функций.
24. Представление многомерно-матричной функции рядом Тейлора.
25. Определение многомерной случайной матрицы, законы распределения многомерной случайной матрицы.
26. Начальные и центральные моменты многомерной случайной матрицы.
27. Математическое ожидание, дисперсионная матрица многомерной случайной матрицы, их свойства.
28. Формулы связи между начальными и центральными моментами многомерной случайной матрицы.
29. Нормально распределенные многомерные случайные матрицы.
30. Многомерные случайные матрицы с совместным нормальным распределением.
31. Принятие решения о многомерной случайной матрице по наблюдению другой многомерной случайной матрицы, случай квадратичной функции потерь.
32. Многомерная модель данных и OLAP-системы.
Общие сведения
Сведения об электронном учебно-методическом комплексе по дисциплине «Анализ многомерных данных»
Электронный учебно-методический комплекс по дисциплине «Анализ многомерных данных» предназначен для студентов специальности 1-53 01 02 "Автоматизированные системы обработки информации".
Электронный учебно-методический комплекс разработан на основе учебной программы «Анализ многомерных данных», утверждённой ректором БГУИР 01 июля 2009 г., регистрационный № УД-53-116/уч.
Составитель:
В.С. Муха, заведующий кафедрой информационных технологий автоматизированных систем (ИТАС) Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники», доктор технических наук, профессор.
Рассмотрен и рекомендован к изданию на заседании кафедры ИТАС, протокол № 16 от 21.06.2011 г.
Одобрен и рекомендован к изданию методическим советом факультета информационных технологий и управления, протокол № 10 от 28.06.2011 г.
Методические рекомендации по изучению дисциплины
Виды занятий и формы контроля знаний определяются рабочей учебной программой дисциплины. Для студентов очной формы обучения предусмотрены лекции в объеме 32 часов, лабораторные работы в объеме 24 часов (6 четырехчасовых лабораторных работ) и экзамен по курсу.
Для студентов дистанционной формы обучения предусмотрена самостоятельная работа над теоретическим материалом дисциплины, две контрольные работы, два индивидуальных практических занятия и экзамен по курсу.
К сдаче экзамена студенты допускаются только при условии выполнения и защиты лабораторных работ (дневная форма обучения), выполнения и защиты контрольных работ и индивидуальных практических занятий (дистанционная форма обучения).
Последовательность изучения материала и выполнения индивидуальных практических занятий и контрольных работ студентами дистанционной формы обучения определяется рабочей учебной программой дисциплины.
Рабочая учебная программа
Учреждение образования
«Белорусский государственный университет
информатики и радиоэлектроники»
УТВЕРЖДАЮ
Декан факультета НИДО
______________ В.М. Бондарик
«______»_________ _______ г.
Регистрационный № УД-____________/р.
АНАЛИЗ МНОГОМЕРНЫХ ДАННЫХ
Рабочая учебная программа для специальности 1-53 01 02 Автоматизированные системы обработки информации
Факультет непрерывного и дистанционного обучения
Кафедра Информационных технологий автоматизированных систем
Курс 6-й
Индивидуальные практические Экзамен 6-й курс
занятия 2
Контрольные работы 2
Всего часов Форма получения
по дисциплине 136 высшего образования дистанционная
Минск 2011
Составил Муха В.С., д.т.н., профессор
Рабочая учебная программа составлена на основе учебной программы "Анализ многомерных данных", утвержденной ректором БГУИР 25.03.2011 г., рег. № УД-53-254/уч., и учебного плана специальности 1-53 01 02 «Автоматизированные системы обработки информации»
Рассмотрена и рекомендована к утверждению на заседании кафедры ИТАС протокол № ___ от «____»___________ г.
Заведующий кафедрой ____________(Муха В.С.)
Одобрена и рекомендована к утверждению Советом факультета ИТУ Учреждения образования «Белорусский государственный университет информатики и радиоэлектроники»
протокол № ____ от «_____»________ _______ г.
Председатель ________________(Л.Ю. Шилин)
СОГЛАСОВАНО
Начальник ОМОУП______________Ц.С.Шикова
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цель преподавания дисциплины. Целью преподавания дисциплины является изложение студентам существующих подходов и методов обработки и анализа многомерных детерминированных и стохастических данных.
Задачи изучения дисциплины. Задачи изучения дисциплины состоят в обзоре существующих подходов к анализу многомерных данных, изложении нового многомерно-матричного подхода и рассмотрении задач, связанных с обработкой многомерных данных.
В результате освоения курса «Анализ многомерных данных» обучаемый должен:
Знать:
- существующие подходы к анализу многомерных данных;
- основные положения многомерно-матричного подхода к анализу многомерных данных;
уметь:
- выполнять математические операции с многомерными данными;
- выполнять программную реализацию методов анализа многомерных данных;
- выбирать программные средства в области анализа многомерных данных;
Иметь представление
- о практических задачах, связанных с анализом многомерных данных;
Перечень дисциплин, усвоение которых необходимо для изучения данной дисциплины.
| № | Название дисциплины | Раздел, тема |
| 1 | Высшая математика | Все разделы |
| 2 | Теории вероятностей и математическая статистика | Все разделы |
| 3 | Вычислительные методы и компьютерная алгебра | Все разделы |
| 4 | Статистические методы обработки данных | Все разделы |
Знания, полученные в рамках данной дисциплины, используются в дипломном проектировании и практической деятельности.
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
| Ку р с | Название и содержание тем (по типовой или учебной программе) | Контрольная работа (номер и тема по п.2) | Индивидуальная практическая работа (по п.1) | Оснащение контрольных, лабораторных и индивидуальных практических работ (по п.4) | Литература (по п.3) | Рекомендуемый объем для изучения (в часах) | Форма контроля знаний |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Раздел 1 Введение. Подходы к анализу многомерных данных | 1–3 | ||||||
| Тема 1. Классический подход к анализу многомерных данных. Понятие многомерных данных. Обзор существующих подходов к анализу многомерных данных. Характеристика классического подхода. | Тема 1. Представление данных рядами Тейлора: классический подход. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 8 | защита и.п.р. | ||
| Тема 2. Подход функционального анализа к анализу многомерных данных. Краткие сведения из функционального анализа и его характеристика | 1–3 | 9 | |||||
| Тема 3. Векторно-матричный и многомерно-матричный подходы к анализу многомерных данных. Характеристика векторно-матричного и многомерно-матричного подходов к анализу многомерных данных. | 1–3 | 8 | |||||
| Раздел 2 Основы многомерно-матричного подхода к анализу многомерных данных. | 1–3 | ||||||
| Тема 4. Определение и структура многомерной матрицы. Определение и структура многомерной матрицы. Транспонирование многомерной матрицы, симметричные многомерные матрицы. | 1–3 | 9 | |||||
Тема 5. Подстановки.
Подстановки на множестве индексов многомерной матрицы как биективные отображения. Суперпозиция подстановок. Некоторые типы подстановок. Операции над многомерными матрицами, ( 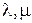 )-свернутое произведение многомерных матриц и его частные случаи. )-свернутое произведение многомерных матриц и его частные случаи.
| 1,4 | 8 | |||||
Тема 6. Формальные правила транспонирования многомерных матриц.
Формальные правила транспонирования многомерной матрицы. Повторное транспонирование многомерной матрицы. Транспонирование ( 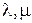 )-свернутого произведения многомерных матриц. )-свернутого произведения многомерных матриц.
| Тема 1. Многомерные матрицы. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 9 | защита к.р. | ||
| Тема 7. Многомерно-матричные полиномы. Многомерно-матричная форма представления полиномов произвольных степеней от многомерно-матричных аргументов. | Тема 2. Многомерно-матричные полиномы. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 8 | защита к.р. | ||
| Раздел 3 Линейные многомерно-матричные алгебраические уравнения. | 1–3 | ||||||
Тема 8. Единичные многомерные матрицы.
Единичные многомерные матрицы. Обратные многомерные матрицы. Матрицы, ( 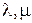 )-ассоциированные с многомерными матрицами. )-ассоциированные с многомерными матрицами.
| 1–3 | 9 | |||||
| Тема 9. Многомерно-матричные линейные алгебраические уравнения. Определитель многомерной матрицы. Многомерно-матричные линейные алгебраические уравнения. | 1–3 | 8 | |||||
| Тема 10. Дифференцирование по многомерно-матричному аргументу. Определение производной многомерно-матричной функции по многомерно-матричному аргументу (многомерно-матричной производной). Повторные производные по многомерно-матричному аргументу. Основные правила многомерно-матричного дифференцирования. | 1–3 | 9 | |||||
| Тема 11. Производные некоторых функций многомерно-матричного аргумента. Производные некоторых функций многомерно-матричного аргумента. Аппроксимация моделей многомерных данных рядами Тейлора. | Тема 2. Представление данных рядами Тейлора: многомерно-матричный подход. | MATLAB 6.5 или MATLAB 7.1 | 1–3 | 8 | защита и.п.р. | ||
| Раздел 5 Случайные векторы, матрицы и многомерные матрицы. | 1–3 | ||||||
| Тема 12. Определения и законы распределения случайного вектора, матрицы, многомерной матрицы. Определения случайного вектора, матрицы, многомерной матрицы, их законы распределения. Гауссовские векторы, матрицы, многомерные матрицы. | 1–3 | 9 | |||||
| Тема 13. Числовые характеристики случайных векторов, матриц, многомерных матриц. Числовые характеристики случайных векторов, матриц, многомерных матриц. Максимально-правдоподобные оценки гауссовских случайных матриц. Апостериорное распределение гауссовских случайных матриц. | 1–3 | 8 | |||||
| Тема 14. Определения и законы распределения векторного и матричного случайных процессов. Определение векторного и матричного случайного процесса, их законы распределения. Моментные функции векторного и матричного случайного процессов. Гауссовские матричные случайные процессы. Оценивание математических ожиданий и ковариационных функций векторных случайных процессов. | 1–3 | 9 | |||||
| Тема 15. Определение, законы распределения и моментные функции скалярного случайного поля. Определение скалярного случайного поля. Законы распределения и моментные функции скалярного случайного поля. Гауссовское случайное поле. Случайное поле, определенное на сетке значений аргументов. Аналогия описаний скалярного случайного поля на сетке значений аргументов и векторного случайного процесса. | 1–3 | 8 | |||||
| Раздел 7 Многомерная модель данных и OLAP-системы. | 1–3 | ||||||
| Тема 16. Реляционная и многомерная модели данных. Модели данных в системах управления базами данных (СУБД). OLAP-системы и 12 принципов Э. Кодда. Многомерная модель данных. Примеры многомерной модели данных | 9 | ||||||
| Итого | 2 | 2 | 136 | Экз. |
ИНДИВИДУАЛЬНЫЕ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ И ИХ ХАРАКТЕРИСТИКА
| № пп | Тема | Содержание | Объем в часах |
| 1 | Представление данных рядами Тейлора: классический подход. | Изучение вопроса аппроксимации функции одной и многих переменных рядом Тейлора на основе классического подхода с привлечением графического представления в Matlab. | 6 |
| 2 | Представление данных рядами Тейлора: многомерно-матричный подход. | Изучение вопроса аппроксимации функции многих переменных рядом Тейлора на основе многомерно-матричного подхода с привлечением графического представления в Matlab. | 6 |
Дата: 2019-02-02, просмотров: 693.