Задача 118. Доказать, что прямая 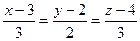 пересекает ось
пересекает ось  и найти точку пересечения.
и найти точку пересечения.
Решение. Если прямая пересекает ось  , то точка пересечения имеет вид
, то точка пересечения имеет вид  . Если в первые две дроби вместо
. Если в первые две дроби вместо  подставить 0, то получим
подставить 0, то получим 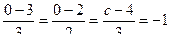 . Тогда
. Тогда  , т.е.
, т.е.  .
.
Если бы первые две дроби после такой подстановки оказались не равны, то это бы означало, что нет пересечения с осью  .
.
Ответ. (0,0,1).
Замечание. Если бы прямая и ось  были скрещивающимися, то подстановка
были скрещивающимися, то подстановка  в канонические уравнения привела бы к противоречию уже в первых двух дробях, например, для
в канонические уравнения привела бы к противоречию уже в первых двух дробях, например, для 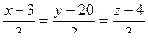 получили бы
получили бы 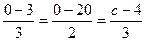 , но ведь
, но ведь 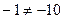 , т.е. противоречие уже в первых дробях, независимо от
, т.е. противоречие уже в первых дробях, независимо от 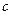 .
.
Практика № 13. Дата 30.10.2018.
Задача 119. Найти точку пересечения плоскости 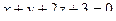 и прямой
и прямой 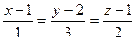 .
.
Решение. Запишем прямую с помощью параметрических уравнений:
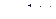 ,
, 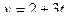 ,
, 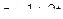 .
.
Подставим эти выражения в уравнение плоскости, чтобы найти, при каком значении  оно выполняется.
оно выполняется. 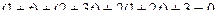

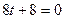

 . Тогда
. Тогда 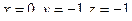 .
.
Ответ. Точка пересечения 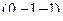 .
.
Нахождение углов.
Задача 120. Найти угол между прямой 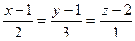
и плоскостью 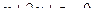 .
.
Решение.
Пусть дана плоскость с помощью уравнения 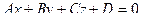 и прямая с помощью точки
и прямая с помощью точки 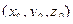 и направляющего
и направляющего 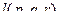 .
.
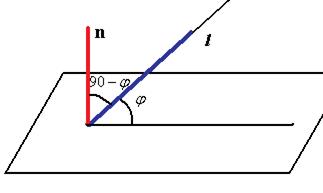
Угол 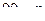 это угол между прямой и нормалью к плоскости.
это угол между прямой и нормалью к плоскости.
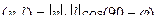 , тогда
, тогда 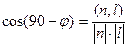 , и в итоге формула:
, и в итоге формула: 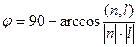 .
.
В данной задаче направляющий к прямой 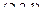 , нормаль к плоскости
, нормаль к плоскости 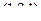 . Их скалярное произведение равно 9.
. Их скалярное произведение равно 9.
Модули векторов равны 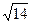 и
и 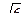 .
. 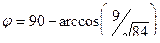 .
.
Приблизительно представим, какой это угол. Если бы было
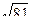 вместо
вместо 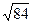 то было бы
то было бы 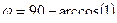 = 90.
= 90.
Но в данном случае дробь чуть меньше, а угол составляет около 79 градусов.
Ответ. 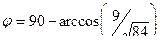 .
.
Задача 121. Доказать, что две прямые в пространстве
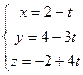 и
и 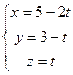 пересекаются, и найти точку пересечения.
пересекаются, и найти точку пересечения.
Решение. Если у них естьь общая точка, то можно приравнять 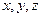 из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах
из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах 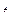 , а во вторых
, а во вторых 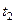 .
.
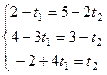 перенесём все
перенесём все 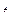 ,
, 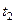 в одну сторону, а константы в другую, чтобы система была записана в стандартной форме.
в одну сторону, а константы в другую, чтобы система была записана в стандартной форме.
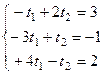 расширенная матрица:
расширенная матрица: 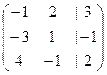
Преобразуем методом Гаусса. От 2-й строки отнимем утроенную 1-ю, а к 3-й прибавим 4-кратную 1-ю.
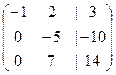 т.е.
т.е. 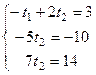 то есть сразу же
то есть сразу же 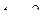 из 2-го и 3-го уравнений, и они не противоречат друг другу. Система совместна, ранги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем
из 2-го и 3-го уравнений, и они не противоречат друг другу. Система совместна, ранги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем 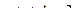 , т.е.
, т.е.  .
.
Впрочем, можно было решить систему ещё быстрее, если сложить 2 и 3 уравнения, тогда сразу бы получилось  .
.
Затем подставить  в первые уравнения либо
в первые уравнения либо 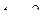 во вторые,
во вторые,
получим одни и те же значения для 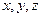 .
.
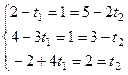 , т.к.
, т.к. 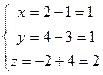 и
и 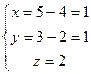
Ответ. Точка пересечения (1,1,2).
Задача 122. Доказать, что две прямые в пространстве:
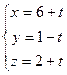 и
и 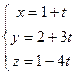 скрещивающиеся.
скрещивающиеся.
Решение. Решая систему уравнений, как в прошлой задаче, здесь мы обнаружим, что система несовместна.
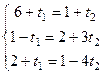

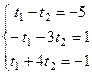 матрица:
матрица: 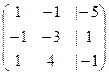
прибавим ко 2-й строке 1-ю, а от 3-й отнимем 1-ю.
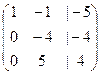 получили систему
получили систему 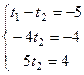
2-е и 3-е уравнения противоречат друг другу. Система не имеет решений, значит, эти 2 прямые не имеют ни одной общей точки.
Так как направляющие векторы 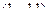 и
и  не коллинеарны, то прямые также и не параллельны. Таким образом, скрещивающиеся.
не коллинеарны, то прямые также и не параллельны. Таким образом, скрещивающиеся.
Полярная система координат.
Кроме пары чисел  , которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим
, которыми можно задать точку на плоскости, можно задать также и таким образом: соединим точку с началом координат, длину этого отрезка обозначим 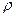 . Угол между осью
. Угол между осью  и этим отрезком обозначим
и этим отрезком обозначим 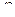 .
.
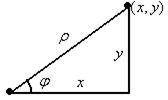
Так как 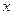 это прилежащий катет, а
это прилежащий катет, а 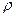 гипотенуза, тогда
гипотенуза, тогда 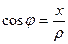 , аналогично
, аналогично 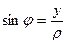 , откуда следуют такие формулы:
, откуда следуют такие формулы: 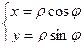
Задача 122. Доказать формулу расстояния между двумя точками в полярных координатах: 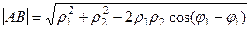 .
.
Решение. Пусть даны две точки, полярные координаты которых соответственно 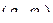 и
и 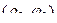 . Выразим их в декартовых координатах:
. Выразим их в декартовых координатах:
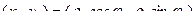 и
и 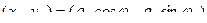 .
.
А в декартовых координатах расстояние считается так:
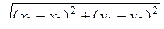 . Тогда получаем:
. Тогда получаем:
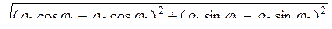 . Выражение под корнем преобразуем и приведём подобные. Оно пока настолько длинное, что занимает две строки:
. Выражение под корнем преобразуем и приведём подобные. Оно пока настолько длинное, что занимает две строки:
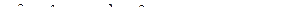 +
+
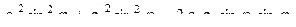 =
=
= 
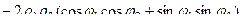 =
=
= 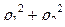
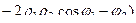 .
.
Итак, 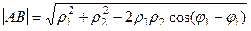 .
.
Задача 124. Найти расстояние между точками, которые заданы в полярных координатах: 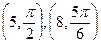 .
.
Решение. По формуле 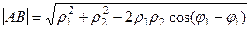 получаем .
получаем . 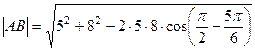 =
=  =
=
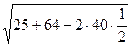 =
= 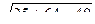 =
= 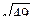 = 7.
= 7.
Ответ. 7.
Задача 125. Построить уравнение прямой 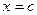 в полярных координатах.
в полярных координатах.
Решение. На чертеже видно, что чем больше угол наклона, тем больше расстояние. При  расстояние
расстояние 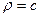 , при
, при 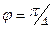 оно увеличивается до
оно увеличивается до 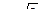 , а затем стремится к
, а затем стремится к 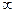 .
.
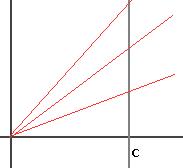
В уравнении 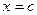 заменим
заменим 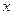 по формулам перехода к полярным координатам, т.е.
по формулам перехода к полярным координатам, т.е. 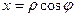 . Получается
. Получается 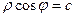 , тогда
, тогда 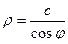 .
.
Замечание. При 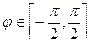 получается
получается  , и точка в правой полуплоскости. Но ведь косинус существует и не только в 4-й и 1-й четвертях, но и во 2-й и 3-й тоже. Но слева нет ни одной точки этой прямой. Нет ли в этом противоречия? На самом деле нет, потому что во 2 и 3 четвертях косинус отрицателен, а при
, и точка в правой полуплоскости. Но ведь косинус существует и не только в 4-й и 1-й четвертях, но и во 2-й и 3-й тоже. Но слева нет ни одной точки этой прямой. Нет ли в этом противоречия? На самом деле нет, потому что во 2 и 3 четвертях косинус отрицателен, а при  надо двигаться в обратную сторону по лучу, направленному влево, тем самым мы снова попадаем вправо, т.е. на ту же самую прямую, и фактически она прочерчивается второй раз.
надо двигаться в обратную сторону по лучу, направленному влево, тем самым мы снова попадаем вправо, т.е. на ту же самую прямую, и фактически она прочерчивается второй раз.
Ответ. 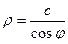
Задача 126. Построить уравнение прямой 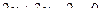 в полярных координатах.
в полярных координатах.
Решение. В уравнении 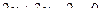 заменим обе переменные
заменим обе переменные  по формулам перехода к полярным координатам. Получится
по формулам перехода к полярным координатам. Получится  , следовательно,
, следовательно,  , откуда следует, что
, откуда следует, что 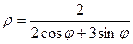 .
.
Ответ. 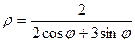 .
.
Задача 127. Построить уравнение окружности 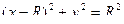 с центром в точке
с центром в точке 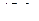 радиуса
радиуса 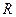 в полярных координатах.
в полярных координатах.
Решение. 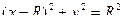

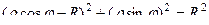



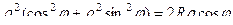

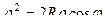

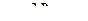 . Чертёж:
. Чертёж:
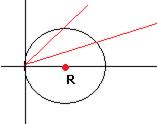
Замечание. Здесь снова, как было в позапрошлой задаче, если луч направлен во 2-ю или 3-ю четверть, при этом косинус отрицателен, а значит, мы попадаем в противоположную сторону - снова на ту же окружность, и она чертится 2-й раз.
Ответ. 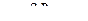 .
.
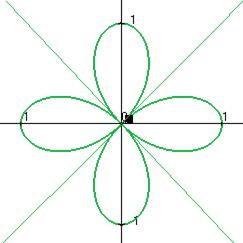
Задача 128. Построить уравнение линии 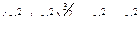 в полярных координатах, сделать чертёж.
в полярных координатах, сделать чертёж.
Решение. В уравнении заменим обе переменные  по формулам перехода к полярным координатам.
по формулам перехода к полярным координатам. 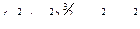

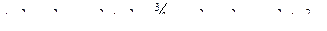

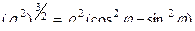

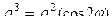

 .
.
Ответ.  .
.
Чертёж:
Практика № 14. Дата: 06.11.2018.
Пункт 129. (теоретическая задача). Выведем формулу 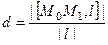 для расстояния от точки до прямой в пространстве.
для расстояния от точки до прямой в пространстве.
Пусть дана прямая (с помощью точки 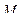 и направляющего
и направляющего 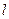 ) и точка
) и точка 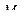 , не лежащая на прямой.
, не лежащая на прямой.
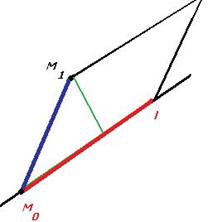
Соединим 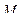 и
и 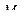 , это одна из двух сторон параллелограмма, вторая это
, это одна из двух сторон параллелограмма, вторая это 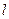 . Требуемое расстояние это высота, тогда надо площадь поделить на длину основания. Площадь равна векторному произведению векторов, образующих стороны.
. Требуемое расстояние это высота, тогда надо площадь поделить на длину основания. Площадь равна векторному произведению векторов, образующих стороны.
Поэтому 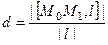 .
.
Закономерен вопрос, а почему требуется выводить новую формулу, если у нас уже была выведена формула расстояния от точки до прямой? Дело в том, что в пространстве уравнение прямой имеет вид не 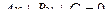 , а канонические или параметрические уравнения, то есть формула
, а канонические или параметрические уравнения, то есть формула 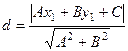 из прошлой темы не применима. В том случае мы пользовались проекцией на нормаль, а в пространстве нормаль к прямой однозначным образом не определяется.
из прошлой темы не применима. В том случае мы пользовались проекцией на нормаль, а в пространстве нормаль к прямой однозначным образом не определяется.
Задача 130. Вычислить расстояние от точки (4,4,-2) до прямой 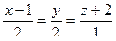 в пространстве.
в пространстве.
Решение. Применим формулу 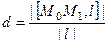 .
.
Точка 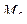 на прямой ищется из таких соображений: все дроби в каноническим уравнении приравняем к 0, тогда
на прямой ищется из таких соображений: все дроби в каноническим уравнении приравняем к 0, тогда 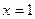 ,
,  ,
, 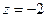 .
.
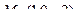 .
. 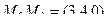 . Направляющий вектор состоит из чисел в знаменателях в канонических уравнениях:
. Направляющий вектор состоит из чисел в знаменателях в канонических уравнениях: 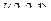 .
.
Его модуль равен  . Векторное произведение:
. Векторное произведение:
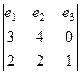 =
= 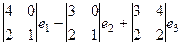 =
= 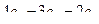 .
.
Модуль этого вектора равен 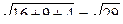 . Ответ.
. Ответ. 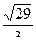 .
.
Задача 131. Даны три точки А(1,1,1),В(2,2,3),С(2,1,2). Вывести уравнение прямой, содержащей АВ, и найти расстояние от точки С
до этой прямой (высота треугольника АВС).
Решение. Вектор АВ (1,1,2) можем принять в качестве направляющего для этой прямой. Он отложен от точки А(1,1,1).
Тогда канонические уравнения прямой: 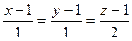 .
.
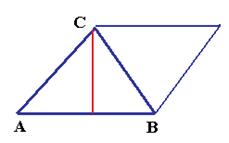
Расстояние в данной ситуации, в пространстве, надо искать по формуле 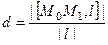 в данном случае
в данном случае 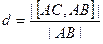 .
.
Здесь точки А,С играют ту же роль, что 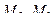 в прошлой задаче.
в прошлой задаче.
2-я сторона параллелограмма: АС=(1,0,1). 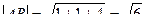 .
.
Векторное произведение:
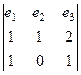 =
= 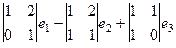 =
=  .
.
Модуль вектора 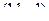 равен
равен 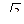 . Тогда результат:
. Тогда результат: 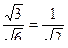 .
.
Ответ. 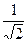 .
.
Пункт 132. (теоретическая задача). Выведем формулу 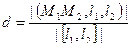 вычисления расстояния между скрещивающимися прямыми.
вычисления расстояния между скрещивающимися прямыми.
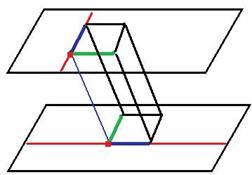
Спроецируем 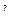 на ту плоскость, где лежит 2 прямая, и
на ту плоскость, где лежит 2 прямая, и 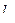 на плоскость, где 1-я. Получается два параллелограмма. Соединим их вершины, получаем параллелепипед.Обратите внимание, что отрезок
на плоскость, где 1-я. Получается два параллелограмма. Соединим их вершины, получаем параллелепипед.Обратите внимание, что отрезок 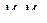 может не являться кратчайшим, так как точки не ровно одна над другой, т.е. углы параллелипепеда могут быть и не 900.
может не являться кратчайшим, так как точки не ровно одна над другой, т.е. углы параллелипепеда могут быть и не 900.
Кратчайшее расстояние = высоте переллелепипеда, то есть d = V / S.
Объём вычислим с помощью смешанного произведения, а площадь основания через векторное от 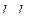 . Итак,
. Итак, 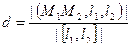 .
.
Задача 133. Найти расстояние между скрещивающимися прямыми: 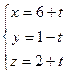 и
и 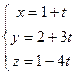 .
.
Решение. Тот факт, что эти прямые скрещивающиеся, мы доказывали (см. задачу 122). На каждой прямой найдём одну точку, присваивая 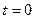 .
.  ,
, 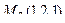 . Вектор, соединяющий две прямых,
. Вектор, соединяющий две прямых, 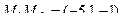 .
.
Вычисляем по формуле 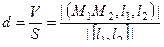 .
.
Смешанное произведение с помощью определителя.
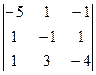 =
= 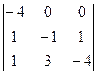 (прибавили 2-ю строку к 1-й)
(прибавили 2-ю строку к 1-й)
= 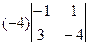 =
=  , а по модулю получается 4.
, а по модулю получается 4.
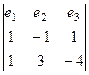 =
= 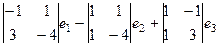 =
= 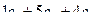 .
.
Модуль векторного произведения равен 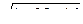 =
=  .
.
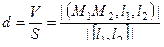 =
= 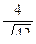 . Ответ.
. Ответ. 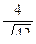 .
.
Задача 134. Заданы 2 прямые в пространстве:
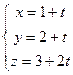 и
и 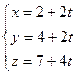 .
.
Доказать, что эти прямые параллельны, и найти уравнение плоскости, содержащей их.
Решение. Во-первых, направляющие векторы (1,1,2) и (2,2,4), что видно из коэффициентов при 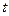 . Они коллинеарны, т.к. координаты пропорциональны.
. Они коллинеарны, т.к. координаты пропорциональны.
Полагая 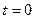 , можем найти хотя бы по одной точке на каждой прямой, а именно M1(1,2,3) и M2(2,4,7). Для построения уравнения плоскости нам нужна 1 точка и 2 неколлинеарных направляющих в плоскости. (1,1,2) и (2,2,4) для этой цели не подходят. В качестве одного направляющего возьмём (1,1,2) а в качестве второго - вектор, соединяющий пару точек на этих прямых, то есть M1M2=(1,2,4).
, можем найти хотя бы по одной точке на каждой прямой, а именно M1(1,2,3) и M2(2,4,7). Для построения уравнения плоскости нам нужна 1 точка и 2 неколлинеарных направляющих в плоскости. (1,1,2) и (2,2,4) для этой цели не подходят. В качестве одного направляющего возьмём (1,1,2) а в качестве второго - вектор, соединяющий пару точек на этих прямых, то есть M1M2=(1,2,4).
Точка в плоскости, например, M1. Итак, проведём плоскость через точку M1(1,2,3) и 2 направляющих: 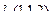 и
и 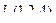 . Третий вектор, проведённый к какой-либо произвольной точке в этой плоскости, и 2 направляющих, образуют ЛЗС:
. Третий вектор, проведённый к какой-либо произвольной точке в этой плоскости, и 2 направляющих, образуют ЛЗС:
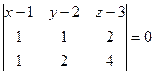

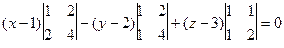

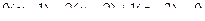

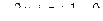

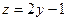 .
.
Ответ. 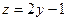 .
.
Пункт 135 (теоретическая задача). Вывод уравнения эллипса.
Определение эллипса. Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний до двух фиксированных точек постоянна.
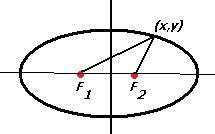
Доказательство (вывод) уравнения эллипса.
Выведем уравнение кривой, удовлетворяющей этому свойству (  = const), и докажем, что в уравнении должна быть сумма квадратов.
= const), и докажем, что в уравнении должна быть сумма квадратов.
Пусть фокусы расположены в точках 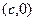 и
и 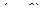 . Вычислим по теореме Пифагора расстояние от точки (x,y) до двух фокусов. F1 расположен дальше длина катета равна
. Вычислим по теореме Пифагора расстояние от точки (x,y) до двух фокусов. F1 расположен дальше длина катета равна  , тогда длина большего из двух отрезков, а именно
, тогда длина большего из двух отрезков, а именно 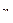 , равна:
, равна: 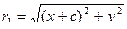 .
.
Фокус F2 наоборот, расположен ближе к точке на чертеже то есть катет на оси Ox равен  , тогда
, тогда 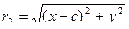 .
.
Выясним, какой именно константе равна величина  . Если расположить точку ровно в правой вершине, то получим
. Если расположить точку ровно в правой вершине, то получим 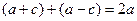 , такая же сумма расстояний по определению должна быть и для произвольных точек. Итак,
, такая же сумма расстояний по определению должна быть и для произвольных точек. Итак,  .
.
Заметим, что если оба корня возвести в квадрат, то они будут отличаться только одним слагаемым, а именно 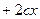 либо
либо 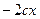 . Тогда можно так оценить разность квадратов:
. Тогда можно так оценить разность квадратов:
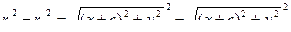 =
= 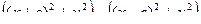 =
=
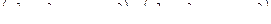 =
=  .
.
Но ведь 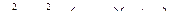 , то есть
, то есть 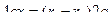 .
.
Тогда мы знаем и разность: 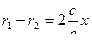 .
.
Итак, получили систему, из которой можно определить каждое 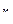 :
:

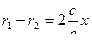
Сложив эти 2 равенства, получим 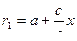 ,
,
а вычитая второе из 1-го, 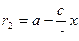 .
.
Сопоставим выражения, изначально полученные по теореме Пифагора, с этими выражениями:
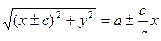 . Теперь возведём в квадрат:
. Теперь возведём в квадрат:
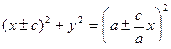 . Тогда
. Тогда 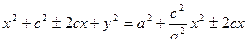 , далее
, далее 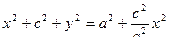 , тогда
, тогда 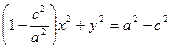

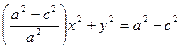

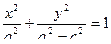 .
.
Рассмотрим вершину 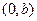 . Сумма расстояний до фокусов равна
. Сумма расстояний до фокусов равна 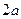 , то есть каждый отрезок, показанный зелёной линией на чертеже, имеет длину
, то есть каждый отрезок, показанный зелёной линией на чертеже, имеет длину 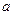 :
:
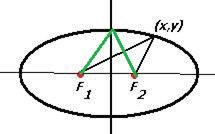
Но ведь он является гипотенузой треугольника, один катет которого это малая полуось (длина  ), а другой -
), а другой - 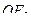 (длина равна
(длина равна 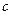 ). Таким образом,
). Таким образом, 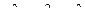 , тогда
, тогда 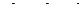 .
.
Итак, каноническое уравнение эллипса: 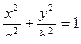 .
.
Задача 136. Доказать, что кривая 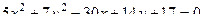
является эллипсом, найти каноническое уравнение, центр и полуоси.
Решение. Выделим полный квадрат по каждой переменной.
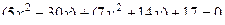

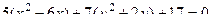 в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ):
в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ): 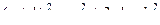 . Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.
. Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.
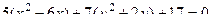

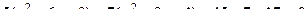

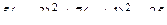

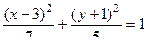

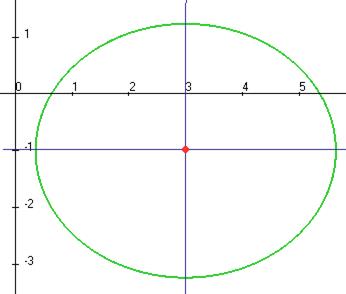
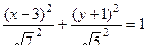 это каноническое уравнение.
это каноническое уравнение.
Ответ. Центр  , полуоси
, полуоси 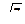 и
и 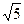 . Чертёж:
. Чертёж:
Практика № 15. Дата: 08.11.2018.
«Введение в математический анализ. Множества и функции»
Задача 137. Доказать нечётность функции 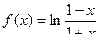 .
.
Решение. Заменим 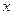 на
на 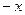 , при этом
, при этом 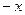 наоборот, заменится на
наоборот, заменится на 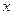 .
.
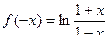 =
= 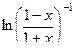 =
= 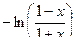 .
.
Таким образом, 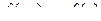 , то есть функция нечётная.
, то есть функция нечётная.
Пункт 138 (теоретическая задача). Докажем, что любая функция 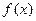 представима в виде суммы чётной и нечётной, то есть
представима в виде суммы чётной и нечётной, то есть 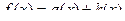 .
.
Доказательство. Введём две функции: 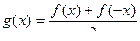 ,
, 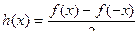 . Первая из них чётна, вторая нечётна. Видно, что если заменить
. Первая из них чётна, вторая нечётна. Видно, что если заменить 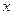 на
на 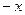 , то для
, то для 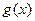 получится выражение, равное исходному, а вот для
получится выражение, равное исходному, а вот для 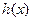 разность в числителе будет противоположна:
разность в числителе будет противоположна: 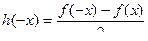 =
= 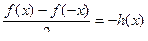 .
.
Сумма этих функций: 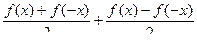 =
= 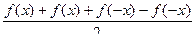 =
= 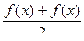 =
= 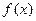 .
.
итак, 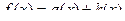 .
.
Если чётную и нечётную компоненты записать для функции  , то получатся так называемые гиперболический косинус и гиперболический синус:
, то получатся так называемые гиперболический косинус и гиперболический синус: 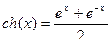 ,
,  .
.
Задача 139. Даны 2 функции:  ,
,  . Найти все их возможные композиции.
. Найти все их возможные композиции.
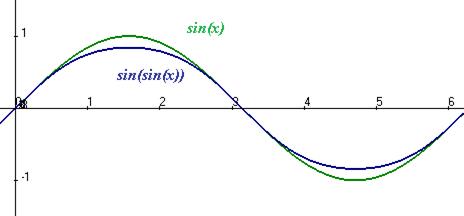
Решение. 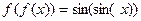 так как
так как  то повторное вычисление синуса ещё чуть уменьшает значение этой величины, поэтому график суть ниже обычного графика синуса.
то повторное вычисление синуса ещё чуть уменьшает значение этой величины, поэтому график суть ниже обычного графика синуса.
Графики для сравнения:
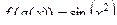 , здесь скорость возрастания с ростом
, здесь скорость возрастания с ростом 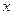 всё более увеличивается, то есть колебания синуса учащаются. График:
всё более увеличивается, то есть колебания синуса учащаются. График:
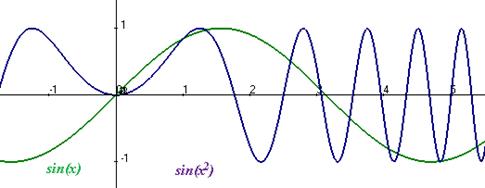
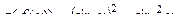 ,график:
,график:
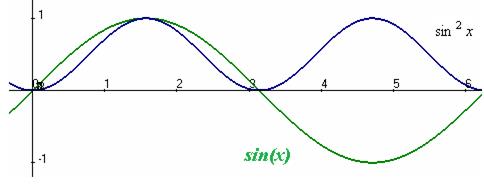
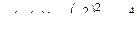 строение этой функции хорошо известно.
строение этой функции хорошо известно.
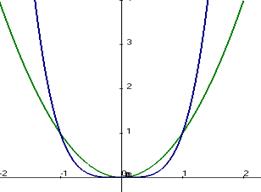
На чертеже зелёным показан график  , синим
, синим 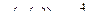 .
.
Задача 140. Найти композицию  если
если 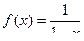 .
.
Решение. Двойная композиция это 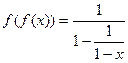 ,
,
а тройная композиция 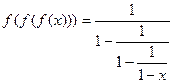 . Можно сначала привести подобные внутри самой внутренней дроби, для чего 1 представим как
. Можно сначала привести подобные внутри самой внутренней дроби, для чего 1 представим как 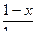 .
.
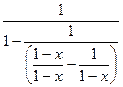 =
=  =
= 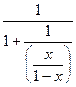 =
= 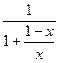
И в этой дроби тоже приведём подобные таким же способом.
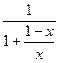 =
= 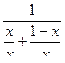 =
= 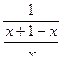 =
= 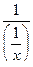 =
= 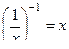 .
.
Ответ. 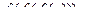 .
.
Задача 141. Точка движется по окружности единичного радиуса вокруг начала координат в плоскости. Температура распределена по закону:
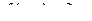 . Найти для этой точки функцию, как меняется температура в зависимости от времени.
. Найти для этой точки функцию, как меняется температура в зависимости от времени.
Решение. Движение точки можно задать так: 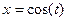 ,
, 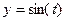 .
.
Подставим эти выражения в 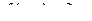 , чтобы получить композицию функций.
, чтобы получить композицию функций.  =
= 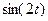 .
.
Ответ. Температура в зависимости от времени для этой точки изменяется так:  .
.
Задача 142. Найти область определения функции: 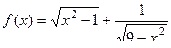 .
.
Решение. Выражение под каждым из корней должно быть  , а для второго даже строго больше 0, так как он в знаменателе.
, а для второго даже строго больше 0, так как он в знаменателе.
Получается система из 2 неравенств:  и
и  .
.
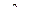

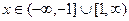 ,
, 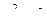

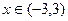 .
.
Итого, пересечение этих множеств: 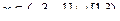 .
.
Ответ. 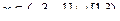 .
.
Задача 143. Найти область определения функции:
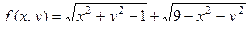 .
.
Решение. Оба подкоренных выражения должны быть неотрицательны
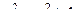 это область вне круга радиуса 1.
это область вне круга радиуса 1.
 это область внутри круга радиуса 3.
это область внутри круга радиуса 3.
В их пересечении лежит кольцо 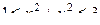 .
.
Чертёж:
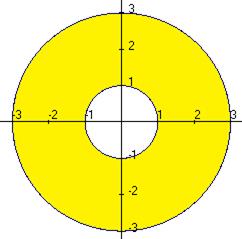
Ответ. Кольцо 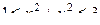 .
.
Задача 144. Найти область определения функции 3 переменных:
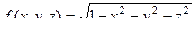 .
.
Решение. Здесь 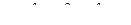 , т.е.
, т.е. 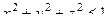 . Это неравенство задаёт шар радиуса 1. Штриховкой в плоскости, как в прошлой задаче, для функции трёх переменных изобразить уже невозможно.
. Это неравенство задаёт шар радиуса 1. Штриховкой в плоскости, как в прошлой задаче, для функции трёх переменных изобразить уже невозможно.
Ответ. Шар радиуса 1: 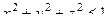 .
.
«Пределы»
Определение. Число 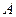 называется пределом последовательности
называется пределом последовательности 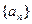 , если:
, если: 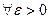
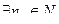 , такое, что
, такое, что 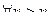 выполняется:
выполняется:  .
.
(для любого числа эпсилон больше нуля, существует такой номер элемента последовательности, что для всех последующих номеров отклонение элементов от числа А меньше, чем эпсилон). В этом случае говорится, что последовательность стремится к числу А.
Обозначение предела:  . (lim это от английского слова limit которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).
. (lim это от английского слова limit которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).
Если рассмотреть полосу от 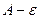 до
до 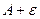 по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:
по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:
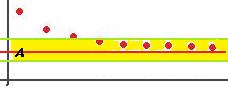
Чем меньше число 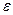 (погрешность меньше) тем больший номер требуется .
(погрешность меньше) тем больший номер требуется .
Пример. 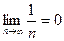 . По определению: если например требуемая точность
. По определению: если например требуемая точность 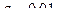 то
то 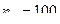 ,
, 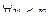 выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.
выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.
* Для того, чтобы лучше понять, что такое предел, представьте следующее. Машина приближается к городу. Для любого заранее заданного расстояния (например 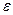 = 10 км.) существует такой момент времени
= 10 км.) существует такой момент времени 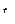 , что в последующие моменты времени
, что в последующие моменты времени  расстояние будет меньше, чем
расстояние будет меньше, чем 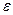 . Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать
. Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать 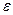 = 5 км. то это достигается в более поздний момент времени, а если
= 5 км. то это достигается в более поздний момент времени, а если 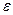 = 1 км. то ещё позже.
= 1 км. то ещё позже.
Предел может и не существовать. Для последовательности 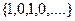 , например, предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа
, например, предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа 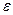 .
.
Задача 145. Найти предел 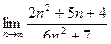 .
.
Решение. Здесь неопределённость типа 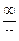 . Вынесем за скобки
. Вынесем за скобки  и в числителе, и в знаменателе, с целью сократить на этот множитель.
и в числителе, и в знаменателе, с целью сократить на этот множитель.
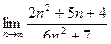 =
= 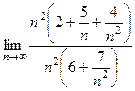 =
= 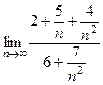
Каждая из мелких дробей в числителе и знаменателе стремится к 0,
поэтому получается сумма пределов в каждом случае, и тогда
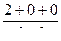 =
= 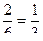 . Ответ.
. Ответ. 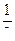 .
.
Предел функции в точке (при 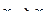 ).
).
Определение. Число 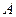 называется пределом функции
называется пределом функции 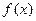 в точке
в точке  , если:
, если: 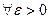
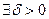 , такое, что при
, такое, что при 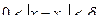 выполняется:
выполняется: 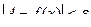 .
.
(для любого числа эпсилон больше нуля, существует такое число дельта, так что если модуль разности  меньше дельта, то модуль разности
меньше дельта, то модуль разности 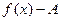 меньше, чем эпсилон).
меньше, чем эпсилон).
Обозначение 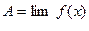 .
.
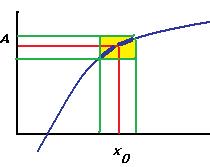
В случае существования предела, получается, что задавая погрешность 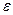 можно найти такой интервал в области определения, что отклонение значений от А будет меньше чем
можно найти такой интервал в области определения, что отклонение значений от А будет меньше чем 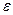 . Фактически, часть графика впишется в некоторый прямоугольник, при уменьшении одной стороны будет уменьшаться и вторая.
. Фактически, часть графика впишется в некоторый прямоугольник, при уменьшении одной стороны будет уменьшаться и вторая.
Задача 146. Найти предел функции 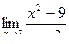 .
.
Решение. В точке 3 значение функции не существует, однако во всех соседних точках существует, и можно узнать, к какой ординате стремится график при 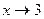 . Разложим на множители:
. Разложим на множители:
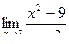 =
= 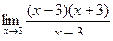 =
= 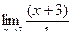 = 6.
= 6.
Тот множитель, который отвечал за стремление к 0 в числителе и знаменателе, сокращён, поэтому далее удалось просто подставить 3 и получить ответ.
Ответ. 6.
Файл обновлён 11.11.2018
Практика № 16. Дата: 13.11.2018.
Практика № 17. Дата: 20.11.2018.
Практика № 18. Дата: 22.11.2018.
Практика № 19. Дата: 27.11.2018.
Практика № 20. Дата: 04.12.2018.
Практика № 21. Дата: 06.12.2018.
Практика № 22. Дата: 11.12.2018.
Практика № 23. Дата: 18.12.2018.
Практика № 24. Дата: 20.12.2018.
Практика № 25. Дата: 25.12.2018.
Дата: 2019-02-02, просмотров: 362.