Задача 114. Построить уравнения прямой в пространстве (канонические, параметрические) по точке 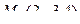 и направляющему вектору
и направляющему вектору 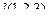 .
.
Решение. Если отложить вектор от 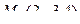 к произвольной точке
к произвольной точке 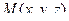 , то вектор
, то вектор  коллинеарен вектору
коллинеарен вектору  , то есть их координаты пропорциональны. Тогда:
, то есть их координаты пропорциональны. Тогда:
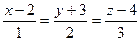
(это мы сейчас получили канонические уравнения).
Обратите внимание, что в знаменателях здесь оказались именно координаты направляющего вектора!
Чертёж:
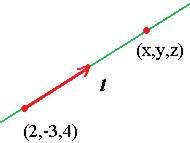
Как мы видим, прямая в пространстве задаётся не одним уравнением, а системой уравнений. Здесь как минимум 2 знака равенства. 1-я дробь равна 2-й, а 2-я равна 3-й. На самом деле здесь даже 3 уравнения, ведь ещё и 1-я равна 3-й.
Если теперь каждую такую дробь приравнять к некоторому параметру 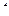 , то:
, то: 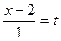 ,
, 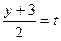 ,
, 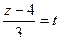 , следовательно:
, следовательно:
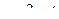 ,
, 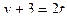 ,
, 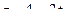 .
.
Тогда 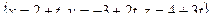 - параметрические уравнения.
- параметрические уравнения.
Можно их записать ещё и в векторной форме: 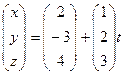 .
.
Они задают движение точки по этой прямой во времени. Здесь при 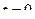 мы как раз оказались бы в исходной точке, а при
мы как раз оказались бы в исходной точке, а при 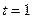 в конце направляющего вектора.
в конце направляющего вектора.
Ответ. 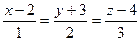 ,
, 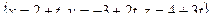
Задача 115. Построить уравнения прямой в пространстве (канонические, параметрические) по двум точкам 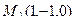 и
и 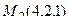
Решение. В качестве направляющего здесь можно рассматривать вектор 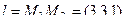 . А далее можно уже делать тем же методом, как в прошлой задаче. Есть точка
. А далее можно уже делать тем же методом, как в прошлой задаче. Есть точка 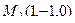 и направляющий
и направляющий 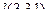 . Информация о 2-й точке при этом уже больше не нужна. Проведём от
. Информация о 2-й точке при этом уже больше не нужна. Проведём от 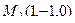 вектор к произвольной точке
вектор к произвольной точке 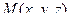 , это вектор
, это вектор 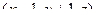 . Он пропорционален вектору
. Он пропорционален вектору 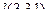 , тогда
, тогда
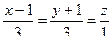
Это и есть канонические уравнения. Параметрические также можно получить с их помощью: 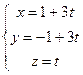 .
.
Ответ. 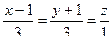 и
и 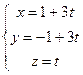 .
.
Задача 116. Построить уравнения прямой, лежащей в пересечении двух плоскостей 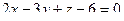 и
и 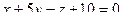 .
.
Решение. Векторное произведение нормалей 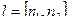 это направляющий вектор, вычислим его.
это направляющий вектор, вычислим его. 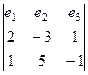 =
=
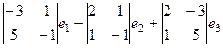 =
= 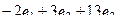 .
.
Итак, направляющий вектор 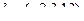 .
.
Теперь нужно найти хотя бы одну точку на этой прямой. Чтобы взять произвольную точку из пересечения плоскостей, можно положить 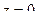 и решить систему, вычислив
и решить систему, вычислив 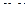 .
.
Два уравнения, без 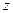 , приводят к такой системе:
, приводят к такой системе: 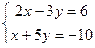 .
.
Выразим из 2-го 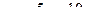 и подставим в 1-е.
и подставим в 1-е.
Получим 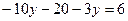 . Тогда
. Тогда 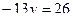 , т.е.
, т.е. 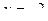 .
.
Но тогда 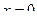 . Итак, получили точку
. Итак, получили точку 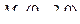 .
.
Вектор от этой точки к произвольной точке 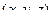 равен
равен  и он пропорционален направляющему вектору. Тогда
и он пропорционален направляющему вектору. Тогда
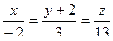 канонические уравнения этой прямой.
канонические уравнения этой прямой.
Приравнивая все эти дроби к  , можно вычислить и параметрические уравнения
, можно вычислить и параметрические уравнения 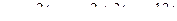 .
.
Ответ.  ,
,  .
.
Задача 117. Найти параметрические и канонические уравнения прямой, перпендикулярной к плоскости треугольника с вершинами 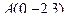 ,
, 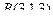 ,
,  и проходящей через вершину А.
и проходящей через вершину А.
Решение. Направляющие АВ и АС это (3,3,0) и 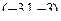 .
.
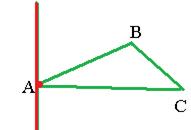
Их векторное произведение:
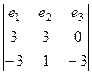 =
= 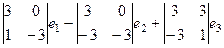 =
= 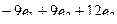 .
.
Итак, вектор 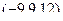 . Но можно в том же направлении выбрать вектор короче в 3 раза (для удобства вычислений) ведь направление от этого не изменится. Итак, пусть направляющий для прямой
. Но можно в том же направлении выбрать вектор короче в 3 раза (для удобства вычислений) ведь направление от этого не изменится. Итак, пусть направляющий для прямой 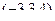 , точка
, точка 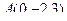 . Вектор от
. Вектор от 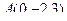 к произвольной точке имеет вид
к произвольной точке имеет вид
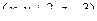 . Он коллинеарен
. Он коллинеарен 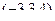 , есть пропорциональность координат. Тогда
, есть пропорциональность координат. Тогда 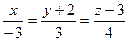 . Это и есть канонические уравнения. Перейти к параметрическим можно так же, как и в прошлых задачах: приравнять все дроби к
. Это и есть канонические уравнения. Перейти к параметрическим можно так же, как и в прошлых задачах: приравнять все дроби к 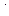 и выразить всё через
и выразить всё через 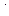 .
.
Ответ. Канонические 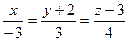 ,
,
параметрические 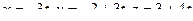 .
.
Дата: 2019-02-02, просмотров: 344.