Любой вектор можно выразить не только как комбинацию базисных векторов, расположенных на осях, например (1,0) и (0,1),
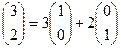
но и как комбинацию какой-то другой линейно-независимой системы.
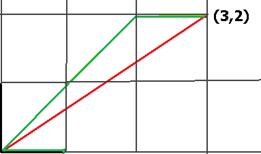
Задача 55. Найти координаты вектора (3,2) в новом базисе, состоящем из векторов (1,1) и (1,0).
Решение. В декартовом базисе координаты (3,2) (пройти 3 шага вправо и 2 вверх), а в новом базисе, состоящем из векторов (1,1) и (1,0) координаты (2,1) (пройти 2 шага по диагонали и 1 шаг вправо).
Найти новые координаты можно так. Запишем их сначала как неизвестные в векторном равенстве:
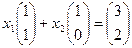а это очевидно, преобразуется к системе: 
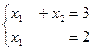. отсюда 
, 
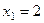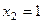. Верно: 
.
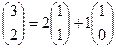Ответ. координаты (2,1).
Задача 56. Даны 3 вектора: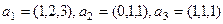 
. Доказать, что они образуют базис в пространстве, и найти новые координаты вектора 
.
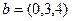Решение. Вычисляя определитель, получим, что он отличен от 0. Затем ищем новые координаты вектора.
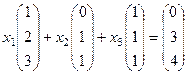система: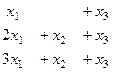 
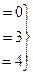
Здесь удобнее получить треугольную структуру ниже не главной, а побочной диагонали. Ведь в третьем столбце все числа 1.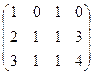 
.
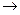
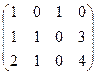
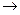
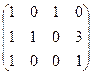Система: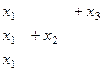 
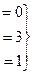. Из 3-го уравнения 
.
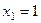Тогда из 2-го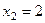 
, а из 1-го уравнения: 
.
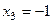Мы поочерёдно выразили их, начиная с 1-го а не последнего, так как нули ниже побочной, а не главной диагонали. Такая модификация метода Гаусса также возможна.
Ответ. Координаты в новом базисе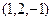 
.
Неопределённые системы (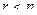 
).
Задача 57. Решить неоднородную систему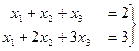 
Решение. Запишем расширенную матрицу, вычтем из 2-й строки 1-ю.
Здесь всего две строки, так что метод Гаусса проводится достаточно коротко.
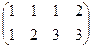
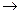
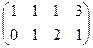
Видим, что базисный минор можно выбрать в первых двух столбцах. Получается, что 3-я переменная свободная. Перепишем снова в виде системы, а не матрицы.
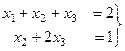переносим 
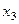вправо: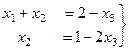 
Выражаем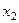 
, а затем поднимаемся в 1-е уравнение и 
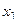,через константы и 
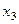. Впрочем, 
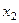фактически и так уже выражено:
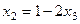. Подставим это выражение в 1-е уравнение
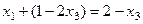, тогда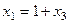 
общее решение системы: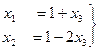 
Также записывается в виде вектора: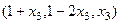 
.
Задавая какое-либо значение 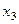, всякий раз можем вычислить остальные переменные, и получить тройку чисел. Частные решения: (1,1,0) или (2,-1,1) или (3,-3,2) ... их бесконечно много.
Ответ. Общее решение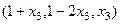 
.
Задача 58. Решить систему уравнений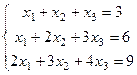 
.
Решение. Запишем расширенную матрицу и преобразуем её методом Гаусса:
.
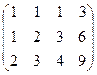
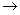
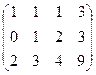
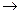
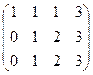
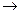
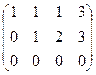Из 2-й строки отняли 1-ю, из 3-й удвоенную 1-ю. Замечаем, что 2 и 3 строка одинаковы, вычитаем из 3-й 2-ю, и 3-я строка получилась состоящей из 0. Это уравнение 0 = 0 , очевидно, его можно вычеркнуть. Базисный минор 2 порядка можно найти в левом верхнем углу. Здесь m = 3, n = 4, r = 2.
Обратите внимание. Типичной и характерной ошибкой является то, что вычёркивают обе пропорциональных строки, а не одну. Но если провести алгоритм Гаусса до конца, то видно, что одна из них остаётся и несёт содержательную информацию, а её копия лишняя, она обратилась в 0. Не нужно торопиться и вычёркивать все пропорциональные строки, ведь хотя бы одна из них не лишняя!
Развернём две оставшихся строки снова в систему уравнений:
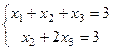
Здесь перенесём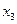 
вправо, 3-я переменная - свободная, базисный минор в левом углу. Замечание. Впрочем, это не единственный вариант: базисный минор можно составить из фрагментов 1 и 3 столбца, тогда 
была бы свободная. Итак, перенесём 
:
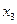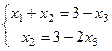Основная матрица системы фактически стала квадратной, 2 порядка, т.е. множество коэффициентов при базисных переменных образует такую квадратную матрицу: 
.
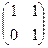Просто справа при этом не только константы, а составные выражения из констант и каких-то параметров. Видно, что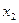 
уже и так выражена, 
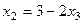. Подставим это выражение в 1-е уравнение, чтобы выразить отдельно 
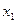через .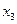
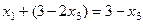в итоге 
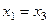. Итак, 
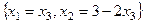- общее решение. В нём есть один свободный параметр .
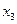Его можно записать также и в виде такого вектора: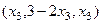 
.
Если задавать любое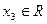 
, будет получать тройки чисел, которые служат частными решениями.
Например, при 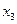= 1 получим (1,1,1). При 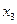= 0 получим (0,3,0). Частных решений бесконечно много.
Ответ. Общее решение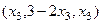 
.
Практика № 7. Дата 02.10.2018.
Задача 59. Решить неоднородную систему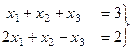 
Решение. Построим расширенную матрицу и преобразуем её.
= 
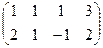
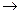
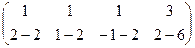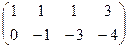
Это равносильно такой системе уравнений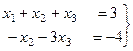 
Базисный минор в первых двух столбцах, 3-й столбец соответствует свободной переменной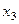 
, её надо перенести вправо.
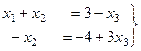теперь надо выразить 
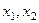через .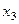
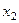фактически и так уже почти выражено, во 2-м уравнении.
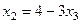. Подставим теперь эту информацию в 1-е уравнение.
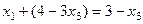, откуда 
.
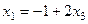Вот эти два выражения ,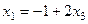
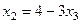
как раз и составляют общее решение системы. Задавая любое значение 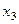, можно вычислить 
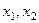, и получится конкретная тройка чисел, то есть частное решение.
Общее решение можно записать также в виде такого вектора: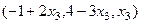 
.
Частные решения, например:
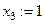
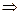частное решение 
.
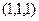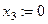
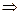частное решение 
.
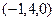Ответ. Общее решение .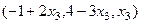
Задача 60. Решить неоднородную систему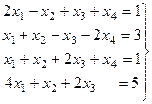 
Решение. Запишем расширенную матрицу системы, впрочем, сразу при этом удобно будет поменять местами 1-ю и 3-ю строки, чтобы угловой элемент содержал именно число 1.
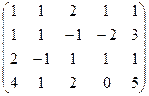
обнулим всё ниже углового элемента, для этого:
из 2-й строки вычтем 1-ю, из 3-й удвоенную 1-ю, из 4-й 1-ю, домноженную на 4.
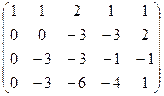
теперь можно поменять местами 2 и 3 строки, а также домножить на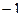 
три последних уравнения (там почти везде были знаки минус)
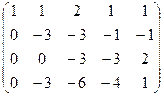
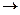
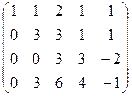
затем из 4-й строки вычитаем 2-ю, чтобы продолжить стандартную процедуру метода Гаусса, потом видим что 3-я и 4-я стали одинаковы, тогда из 4-й вычитаем 3-ю. Получается, что 4-е уравнение 0 = 0.
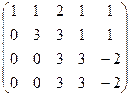
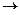
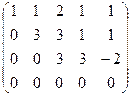
Итак, осталось 3 уравнения, базисный минор легко заметить в первых трёх столбцах (там треугольная структура матрицы, и этот определитель явно отличен от 0). 4-й столбец не входит в базисный минор, то есть 4-я переменная свободная, т.е. когда будем записывать систему, переносим её через знак равенства во всех уравнениях.
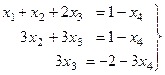
Из последнего уравнения 
, подставляя это выражение во 2-е уравнение, выразим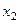 
. 
= 
,
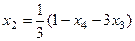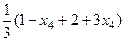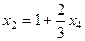. Далее из 1-го уравнения:
= 
,
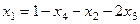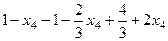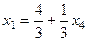. Итак, общее решение:
, 
, .
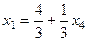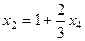Можно записать в виде вектора: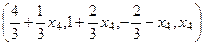 
.
Если задать, например,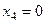 
получим частное решение: 
.
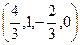Ответ. Общее решение: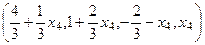 
.
Однородные системы.
Задача 61. Решить однородную систему:
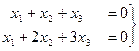
Решение. Видим, что отличие от предыдущей задачи в том, что справа нулевые константы. Если преобразовывать расширенную матрицу, то получим:
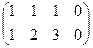
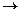
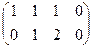
Видим, что справа всё равно как был, так и остаётся столбец из нулей, так что в будущем для однородных систем можно использовать только основную матрицу, ведь расширенная не несёт никакой новой информации, всё равно там справа нулевой столбец, и он не меняется при преобразованиях строк.
Итак, получили систему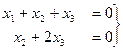 
базисный минор можно заметить в первых двух столбцах, так что 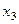свободная переменная, переносим её вправо: 
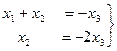. Теперь последовательно выражаем через свободную переменную две базисные переменные.
Из 2-го: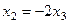 
, а подставляя в 1-е, получим
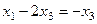, т.е. 
.
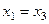Общее решение системы :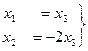 
.
Также записывается в виде вектора: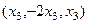 
.
Отличие от прошлой задачи в том, что на всех местах, где там были константы, здесь 0. Все переменные преобразовывались точно так же.
Частные решения здесь отличаются тем, что задавая 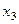в k раз больше, мы и все остальные получим тоже в k раз больше:
, 
, 
, 
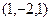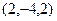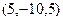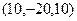и так далее.
То есть все тройки чисел будут пропорциональны какой-то одной.
Если для неоднородной системы представить эти тройки чисел как точки в пространстве, то там они образовывали прямую,не проходящую через начало координат, а для однородной системы - проходящую через начало координат. Поэтому разумно выбрать для этой прямой всего 1 вектор, который задаёт её. Это как раз и есть ФСР (фундаментальная система решений). ФСР .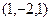
Ответ. Общее решение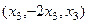 
, ФСР .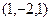
Задача 62.Решить систему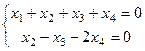 
Решение. Минор, состоящий из 1 и 2 столбцов, уже в треугольной форме. Базисный минор порядка 2. Тогда 3-я и 4-я переменная - свободные. Перенесём их через знак равенства.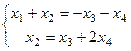 
.
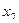уже фактически выражено: 
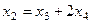, подставим это в первое уравнение, чтобы выразить 
.
.
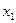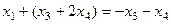
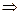
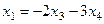Общее решение: { , }.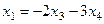
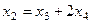Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.
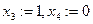, получим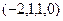 
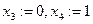, получим 
.
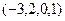Эти 2 вектора { 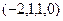, 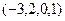} и есть ФСР. Это 
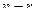частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение { , }.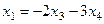
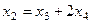ФСР { , }.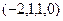
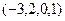Замечание. Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа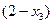 
. А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
Задача 63. Решить однородную систему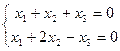 
.
Решение. Можно записать основную матрицу и там вычесть 1-ю строку из 2-й, впрочем, можно для небольшой системы сделать это и сразу в системе, вычесть 1-е уравнение из 2-го. Получится:
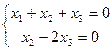
Ранг равен 2, а неизвестных 3, 3-я неизвестная свободная, переносим вправо. Тогда: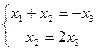 
Из 2-го уравнения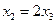 
, тогда 
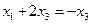, а значит 
.
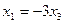Общее решение: 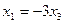, 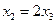. В виде вектора: 
.
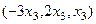Присвоим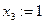 
, получим остальные неизвестные.
ФСР состоит всего из одного вектора: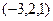 
. Все остальные решения пропорциональны этому.
Если бы, например, присвоили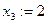 
, получили бы 
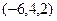. Это потому, что всего одна свободная переменная.
Ответ. Общее решение: 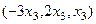, ФСР .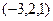
Задача 64. Решить однородную систему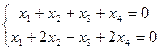 
Решение. Запишем основную матрицу, преобразуем её.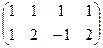 
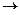
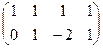
снова представим в виде системы: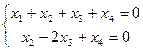 
базисный минор порядка 2, можно обвести в левом углу, поэтому 3-я и 4-я переменная - свободные. Здесь их уже две, так как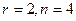 
, поэтому 
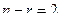. Перенесём их через знак равенства.
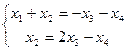
здесь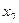 
уже выражено: 
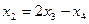, подставим это в первое уравнение, чтобы выразить и .
, 
.
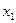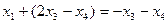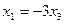Общее решение: , .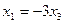
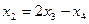В виде вектора: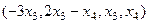 
.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как число 1 в них на разных местах.
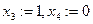, получим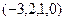 
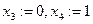, получим 
.
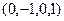Эти 2 вектора { ,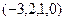 
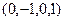} и есть ФСР. Это 
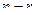частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение: .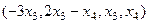
ФСР это множество из 2 векторов: {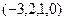 
, }.
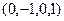Задача 65. Решить однородную систему, найти ФСР.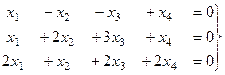 
Решение. Запишем основную матрицу системы и преобразуем её методом Гаусса.
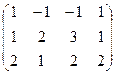
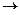
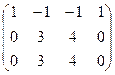
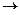
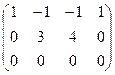
Ранг матрицы равен 2, базисные столбцы 1-й и 2-й. Несмотря на то, что сначала могло показаться, что здесь будет одна свободная переменная (4 переменных и 3 уравнения), на самом деле здесь будет две свободных переменных, ведь 3-е уравнение оказалось линейной комбинацией первых двух.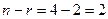 
.
Снова возвращаемся от матрицы к системе уравнений.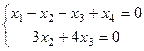 
перенесём свободные неизвестные вправо:
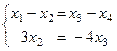из 2 уравнения 
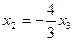, подставим это в 1-е,
будет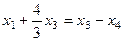 
, то есть 
.
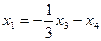Общее решение: , .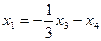
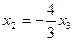В виде вектора: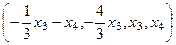 
Построим ФСР из 2 векторов.
, получим 
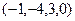
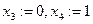, получим 
.
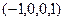Так как здесь есть дроби, то для того, чтобы векторы в ФСР содержали только целые координаты, можно задавать не только 1, но и другое число, главное только чтобы в 3 и 4 координатах помещался невырожденный минор. Если мы задаём поочерёдно каждой свободной переменной какое-то число (не обязательно 1) а остальным 0, то линейная независимость этой системы векторов всё равно заведомо обеспечена.
Ответ. Общее решение: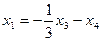 
, .
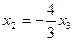ФСР из 2 векторов: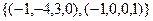 
.
Задача 66. Решить однородную систему, найти ФСР.
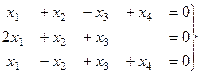
Решение. Преобразуем методом Гаусса основную матрицу системы.
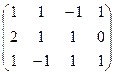
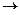
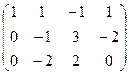
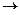
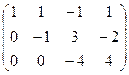
Треугольная структура продолжилась до самой последней строки, и не проявилась строка из нулей, то есть ранг равен 3. Здесь всего одна свободная переменная. Развернём обратно эту матрицу, т.е. запишем в виде системы, а затем перенесём свободные переменные вправо.
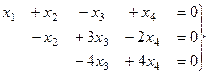
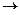
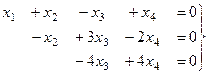
Из последнего,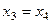 
, это подставим во 2-е и получим 
.
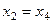Затем это всё в 1-е уравнение, получим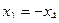 
.
ФСР: один вектор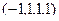 
.
Ответ. Общее решение: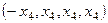 
. ФСР: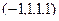 
Задача 67. Решить однородную систему, найти ФСР.
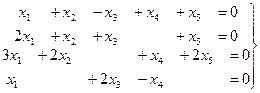
Решение. Преобразуем методом Гаусса основную матрицу системы.
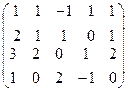
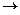
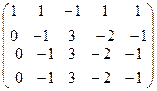далее можно вычесть 2 строку из 3-й и 4-й, и там везде будут 0.
Здесь ранг 2, неизвестных 5,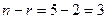 
.
Переписывая в виде системы, переносим вправо 3 свободных переменных.
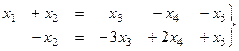
Выражаем из 2-го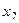 
как линейную функцию от 
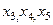, а затем с помощью 1-го уравнения, также и 
.
, 
.
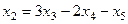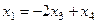Общее решение: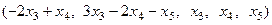 
.
ФСР из 3 векторов. Для этого задаём поочерёдно 1 какой-либо из свободных переменных, а 0 остальным.
ФСР: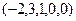 
, 
, 
.
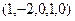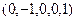Ответ. Общее решение: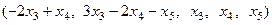 
.
ФСР: , ,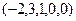 
.
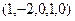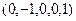Рекомендуемые домашние задачи!
Задача Д-17. Решить однородную систему, найти ФСР:
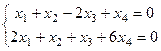
Ответ. Общее решение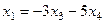 
, 
.
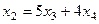ФСР (-3,5,1,0) и (-5,4,0,1).
Задача Д-18. Решить однородную систему, найти ФСР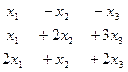 
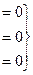
Ответ. Общее решение: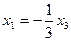 
, 
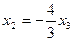, ФСР: 
.
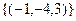Практика № 8. Дата 09.10.2018.
Элементы векторной алгебры.
Задача 68. Найти скалярное и векторное произведение векторов (1,1,1) и (1,2,3) .
Решение. Скалярное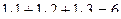 
.
Векторное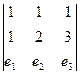 
= 
= .
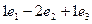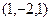Ответ. Скалярное 6, векторное (1,-2,1).
Замечание. Можно проверить, что (1,-2,1) перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0).
Задача 69. Найти скалярное и векторное произведение векторов:
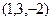и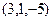 
.
Решение.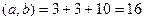 
.
Для поиска векторого произведения запишем определитель.
= 
= 
.
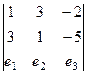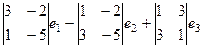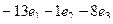Ответ. Скалярное: 16, векторное: (-13, -1, -8).
Задача 70. Дано: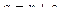 
, 
, 
, 
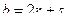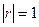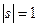, угол между векторами 
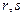45 градусов. Найти 
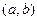и 
.
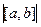Решение.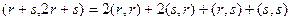 
= 
= 
.
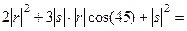
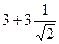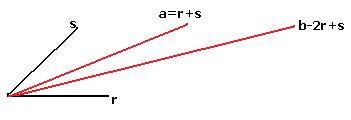
Примечание. Как видим, можно вычислять скалярное произведение, даже не зная координат векторов. Здесь фактически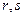 
служат в качестве базисных векторов, и через них выражены 
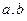, то есть (1,1) и (2,1) координаты 
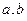относительно базиса 
. Вся эта система целиком может двигаться или вращаться, но углы между векторами и их длины при этом не поменяются. Поэтому конкретных координат и нет, и они для решения задачи и не нужны.
Пункт Б. =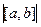 
= 
=
= 
= 
.
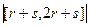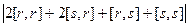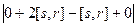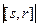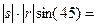
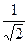Ответ. 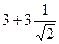и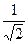 
.
Задачи 71,72,73. Векторы a,b выражены через p,r: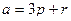 
, 
. 
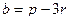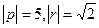, угол между ними 45 град.
Задача 71. Найти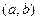 
. Задача 72. Найти | [a,b] |.
Задача 73. Найти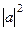 
.
Решение задачи 71.
= 
= 
.
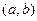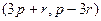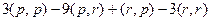Мы раскрыли скобки, используя свойства скалярного произведения. Далее, так как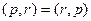 
то объединим их, и получим 
.
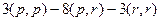Это можно выразить так:
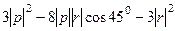и получаем 
.
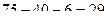Ответ. 29.
Решение задачи 72.
= 
= 
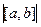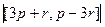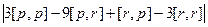
Несмотря на то, что скобки мы раскрыли похожим образом, дальше будет существенное отличие, т.к. свойства векторного произведения совсем другие, чем скалярного. Так,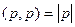 
, но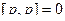 
. Кроме того, чтобы объединить 
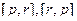в одно слагаемое, здесь надо сначала у одной из них сменить знак.
= 
=
= 
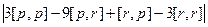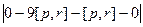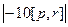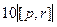. Модуль векторного произведения 
и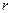 
это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так:
= 
= 
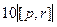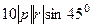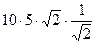= 50. Ответ. 50.
Решение задачи 73.
= 
= 
= 
=
= 
=
= 
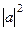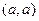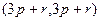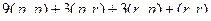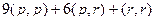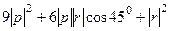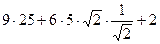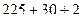= 257. Ответ. 257.
Задача 74. Найти смешанное произведение трёх векторов:
.
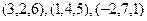Решение. Вычислим определитель:
= 
= 
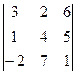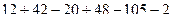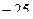. Ответ. 
.
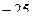Задача 75. Найти косинус угла между векторами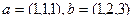 
.
Решение.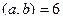 
, 
, 
,
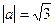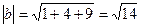учитывая ч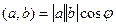то 
, то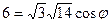 
.
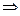
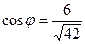Заметим, что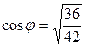 
, т.е. чуть меньше 1, угол близок к 0.
Ответ. .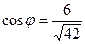
Задача 76. Найти косинус угла между векторами 
.
Решение.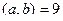 
, 
, 
,
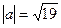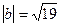учитывая ч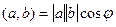то 
, то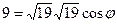 
.
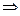
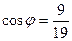Оценим приблизительно, какой это угол. Заметим, что если было бы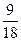 
то было бы 
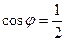и угол 600.
В данном случае косинус чуть меньше, а значит угол чуть больше 600.
Ответ.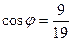 
.
Задача 77. Вычислить площадь параллелограмма, образованного векторами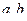 
, если 
, 
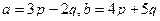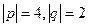, угол между p,q равен 
.
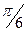Решение.
Площадь параллелограмма - значит, надо вычислить модуль векторного произведения =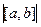 
= 
=
= 
= 
= 
=
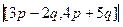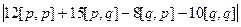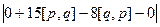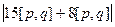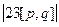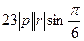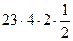= 92.
Ответ 92.
Практика № 9. Дата 12.10.2018.
Задача 78 и 79. Векторы a,b выражены через p,q: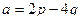 
, 
. 
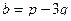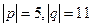, угол между ними 600.
Задача 78. Найти .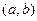
Решение. =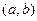 
= 
= 
= 
=
= 
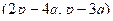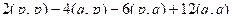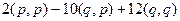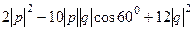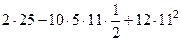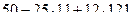= 1227.
Ответ. 1227.
Задача 79. Найти | [a,b] |.
Решение.
| [a,b] | = |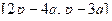 
|= | 
| = | 
| = | 
| = 
=
= 
.
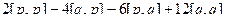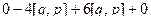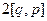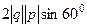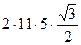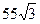Ответ. .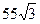
Задача 80.
Доказать неравенство Коши-Буняковского: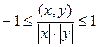 
.
Решение. Рассмотрим скалярное произведение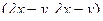 
. Так как здесь умножается один и тот же вектор на себя, то оно неотрицательно: 
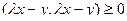. По свойствам скалярного произведения, раскроем скобки:
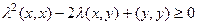
А теперь рассмотрим это выражение как неравенство с квадратичным трёхчленом относительно переменной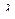 
. Для каждых конкретных векторов 
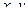то это неравенство приобретает вид: 
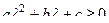, где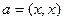 
, 
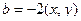
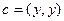. Если выражение больше ири равно 0, то значит, для самого квадратичного уравнения нет корней или всего 1 корень, но не 2 корня. То есть, дискриминант меньше или равен 0. Тогда 
= 
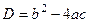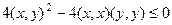, тогда
.
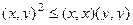
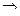
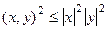
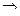
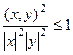Извлечём корень и получим .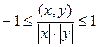
Задача 81. Вывести формулу проекции вектора на ось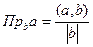 
.
Решение. 1) известно, что 
.
2) длина проекции 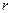это катет, 
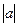гипотенуза треугольника, тогда получается, что 
.
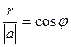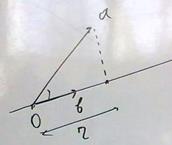
Сопоставим эти 2 факта.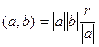 
, тогда 
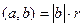, откуда и следует 
.
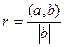Задача 82. Найти проекцию вектора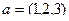 
на линию, порождаемую вектором 
.
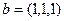Решение. По формуле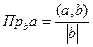 
= 
= 
= 
.
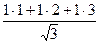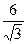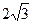Ответ. .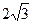
Линейные операторы.
Вспомним, что при умножении квадратной матрицы на столбец, один вектор преобразуется в другой. Получается, что квадратная матрица задаёт некоторое отображение одних векторов в другие, то есть выступает в роли функции.
Отображение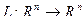 
называется линейным отображением (синоним: линейный оператор) если выполнены 2 условия:
1) 
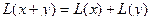2) 
.
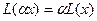Умножение квадратной матрицы на вектор удовлетворяет свойствам линейности, в силу свойств умножения матриц.
Из определения напрямую следует, что всякое линейное отображение зависит только от того, куда отображаются базисные векторы: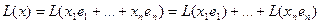 
= 
.
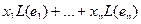Образ вектора x в итоге зависит от координат вектора x и от образов базисных векторов, то есть линейный оператор однозначно задаётся образами базисных векторов.
Дата: 2019-02-02, просмотров: 338.
