Докажем, что образы базисных векторов расположены в столбцах матрицы, что именно при таком строении матрицы умножение её на вектор-столбец будет задано корректно, то есть оно будет действительно отображать базисные векторы в их образы.

Умножим произвольную квадратную матрицу на 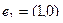и : , .

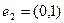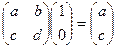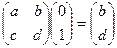       Базисные векторы при умножении на квадратную матрицу отобажаются именно в такие векторы, координаты которых записаны в 1 и 2 столбце матрицы. Строение матрицы оператора: столбцы есть образы базисных векторов при данном отображении, то есть столбец номер 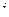 матрицы оператора содержит вектор .

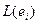       Итак, если задан какой-либо закон, по которому отображаются векторы, то чтобы задать матрицу оператора, надо найти, куда отображаются базисные векторы.

Задача 83. Найти матрицу оператора поворота плоскости на угол .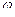

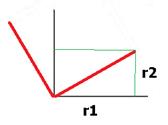
Решение. Красным показаны образы базисных векторов. Но мы повернули именно единичный вектор, т.е. 1 это длина гипотенузы, отмеченной красным. Тогда расстояния r1 и r2 равны 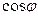 и .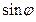

Для образа вектора 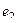 соответственно,  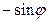и .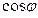

Получаем матрицу .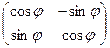

Ответ. .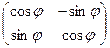

При 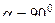  получится  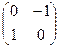Действие оператора на любой вектор задаётся матрицей так:  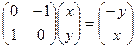- любой вектор поворачивается на 90 градусов.

При 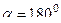 матрица будет иметь вид 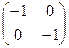, и действительно, умножение на такую матрицу переводит любой вектор  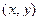в 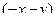, а при повороте на  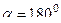каждый вектор как раз и должен повернуться и стать противоположным исходному.

Задача 84. Построить матрицу линейного оператора проекции 3-мерного пространства на плоскость .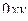

Решение. Найдём, куда переходят 3 базисных вектора. Первые 2 из них остаются на своих местах, 3-й обращается в 0.

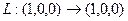
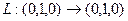
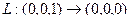
Эти числа запишем в столбцы матрицы оператора.

Ответ. .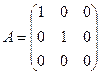

Матрица вырожденная, оператор не является обратимым.

Задача 85. Построить матрицу линейного оператора в 2-мерном пространстве, если действие оператора задано таким образом: .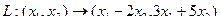

Решение. Находим, в какие векторы отображаются два базисных вектора: , .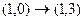

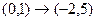Эти результаты запишем по столбцам: .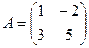

Ответ. Матрица линейного оператора .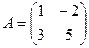

Проверка: 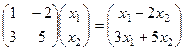. То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу.

Так, 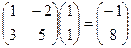  но ведь и по исходным формулам  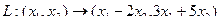получилось бы то же самое: .

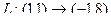Задача 86. Построить матрицу линейного оператора в 3-мерном пространстве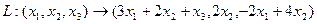

Решение. Отобразим базис 3-мерного пространства.

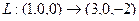
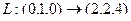
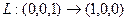
Ответ. Матрица линейного оператора .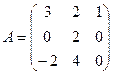

Задача 87. Найти матрицу оператора 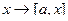, отображающего каждый вектор в его векторное произведение на какой-то фиксированный вектор .

Решение.   Отобразим базис.

Сначала найдём, куда отобразится вектор (1,0,0).

 =  =

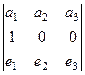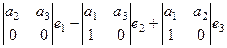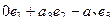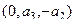 =  это и есть 1-й столбец матрицы оператора.

Аналогично, для нахождения 2 столбца надо отобразить (0,1,0).

 =  =

 = .

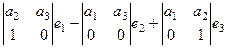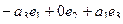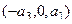Для третьего вектора

 =  =

 = .

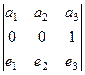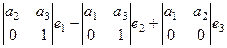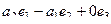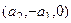Ответ. .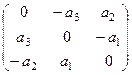

Практика № 10. Дата 16.10.2018.