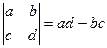.
Пример с наглядным геометрическим смыслом.
= 
.
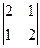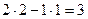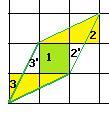
Для параллелограмма, построенного на базе системы векторов (2,1) и (1,2), площадь равна 3. Если область 2’ перенести в область 2, то видно, что получается половина прямоугольника площади 2 (выделено жёлтым). То есть площадь равна 1. Аналогично 3’ в 3. Там тоже площадь 1. Кроме того, в центре квадрат площади 1.
Задача 8. Найти определитель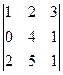 
(можно любой аналогичный пример с другими числами).
Решение. Допишем копии первых двух столбцов, проведём 3 параллельных линии (главная диагональ и ещё две). Перемножим все эти тройки элементов и внесём в общую сумму с их исходным знаком. А вот для побочной диагонали и линий, ей параллельных, со сменой знака.
=
.
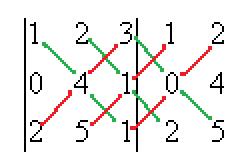
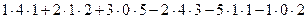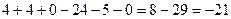Ответ.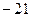 
.
Практика № 2. Дата 11.09.2018.
Задача 9А. Найти произведение: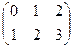 
.
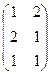Задача 9Б.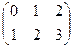 
.
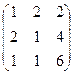Решение. В 1-м случае размеры 
и 
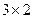, согласованы, умножение возможно. Во 2-м случае 
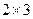и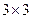 
, тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.
= 
=
= 
.
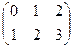
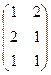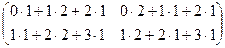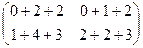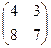Для 3Б 1-я и 2-я строка умножаются не только на 1-й и 2-й, но ещё и на 3-й столбец. Дополнительно получаем
= 
= 
.
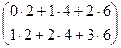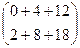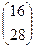Выделим красным цветом новый столбец:
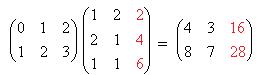
Ответ. 9А: 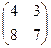, 9Б: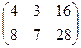 
.
Задача 10. Даны матрицы
, 
, 
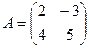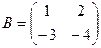. Найти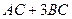 
.
Решение. Так как матрица С находится справа во всех слагаемых, то для удобства можно использовать приведение подобных =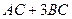 
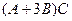- тогда умножение надо будет проводить всего один раз, а не два.
Сначала запишем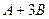 
.
= 
= 
.
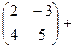
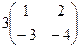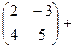
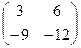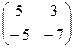Теперь умножим на матрицу С. Точно так же, как и в прошлом примере, мысленно обведём строку из 1-й матрицы на столбец из 2-й.
Есть 4 варианта это сделать:
= 
= 
= 
.
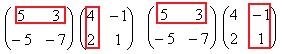
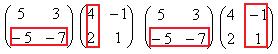
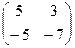
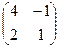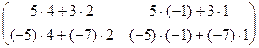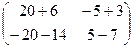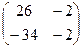Ответ.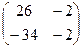 
.
Задача 11. Даны матрицы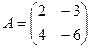 
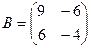. Найти 
.
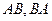Решение.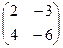 
= 
= 
.
= 
= 
.
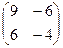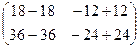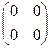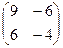
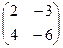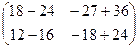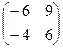Ответ.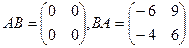 
.
Задача домашняя № Д1.
Найти произведение матриц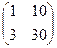 
.
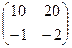(Ответ: нулевая матрица)
Задача 12. Даны матрицы:
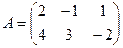
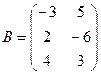Найти .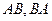
Решение.
= 
= 
.
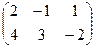
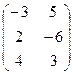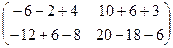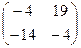Теперь поставим их наоборот, но при этом произведением будет уже не матрица 2 порядка, а матрица 3 порядка: теперь у первой 3 строки, но более коротких, а у второй 3 столбца. Вариантов умножить строку на столбец будет 9.
= 
= 
.
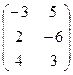
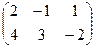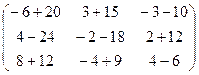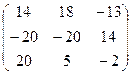Ответ.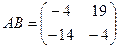 
, 
.
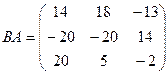Задача 13. Даны матрицы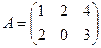 
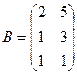. Найти .
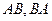Решение.
= 
= 
.
= 
= 
.
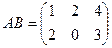
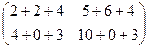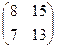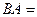
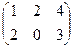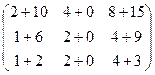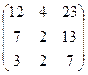Ответ.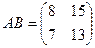 
, .
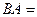
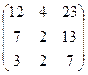Задача 14. Дана матрица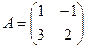 
. Найти 
.
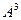Решение. Сначала умножим две, и найдём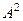 
.
= 
= 
.
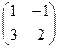
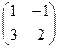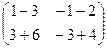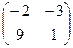Теперь домножим ещё на одну матрицу А, чтобы найти .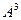
= 
= 
.
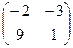
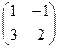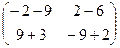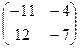Ответ. .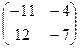
Замечание. Несмотря на то, что в общем случае коммутативности по умножению матриц нет, но если матрица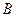 
совпадает с матрицей 
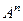, тогда 
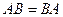. Например, в этой задаче, 
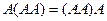из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.
Домашняя № Д2. Найти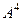 
для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить 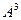, полученную в прошлой задаче, ещё раз на 
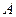, либо взять 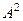, полученную на первом этапе, и её умножить саму на себя. Ответ. 
.
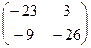Задача 15. Найти произведени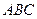е 
, где
, 
, 
.
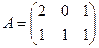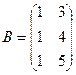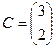Решение. Вычислим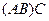 
, сначала умножим первые две матрицы:
= 
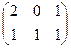
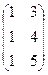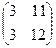. Теперь умножим на третью матрицу.
= 
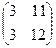
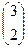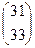. Ответ. .
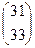Замечание. Если вычислять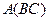 
, то получается точно такой же результат, т.к. выполняется закон ассоциативности.
Замечание. При умножении квадратной матрицы на вектор-столбец получается снова вектор-столбец, то есть квадратная матрица фактически выступает в роли функции, отображающей векторы в пространстве (или на плоскости, если n = 2).
Определители.
Задача 16. Найти определитель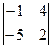 
.
Решение. =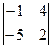 
.
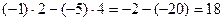Ответ. 18.
Задача 17. Найти определитель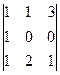 
.
Решение.
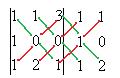
То, что перемножено по зелёным линиям, включим в сумму со знаком плюс, а по красным - со знаком минус.
= 
.
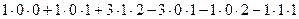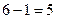Ответ. 5.
Задача 18. Найти определитель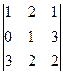 
.
Решение.
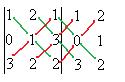
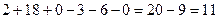. Ответ. 11.
Практика № 3. Дата 14.09.2018.
Задача 19. Найти определитель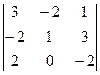 
.
Решение.
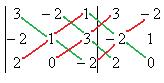
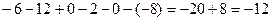. Ответ. 
.
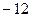Задача 20. Найти параметр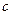 
, при котором определитель равен 0:
.
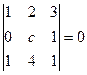Решение. Вычислим определитель и решим получившееся уравнение:
, 
, 
, 
.
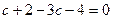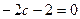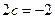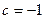Ответ. .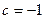
Задача 21. Найти объём тетраэдра, вершины которого
A(1,1,1), B(2,1,3), C(2,2,4), D(1,2,4).
Решение. Объём тетраэдра ровно в 6 раз меньше объёма параллелепипеда с рёбрами AB, AC, AD.
Найдём эти векторы, и сначала вычислим объём параллелепипеда с помощью определителя, затем поделим на 6.
AB = (1,0,2), AC = (0,1,3), AD = (1,1,3).
= 
, 
.
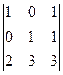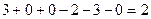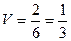Ответ. Объём тетраэдра равен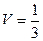 
.
Задача 22. Вычислить определитель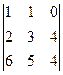 
с помощью разложения по первой строке.
Решение. Выберем дополняющий минор для каждого элемента 1-й строки, и домножим на 
=
= 
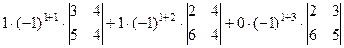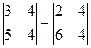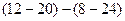= 8. Ответ. 8.
Важное свойство: если к любой строке прибавить другую строку, домноженную на число,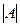 
не изменится.
Доказательство.
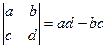. Рассмотрим 
=
.
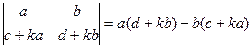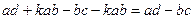Геометрический смысл. Если к вектору b прибавить вектор a, умноженный на любой коэффициент, то площадь параллелограмма не изменится, основание и высота остались старыми, см. чертёж:
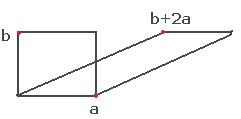
Здесь площадь параллелограмма, образованного векторами a,b такая же, как для образованного векторами a, b+2a.
Задача 23. Вычислить определитель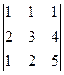 
методом Гаусса (приведением к треугольной форме) используя свойство, указанное выше.
Решение. Вычитаем из 2-й строки удвоенную 1-ю, и из 3-й 1-ю.
= 
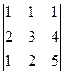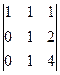затем вычитаем из 3-й строки 2-ю.
получили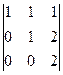 
= 2. Ответ. 2.
Дата: 2019-02-02, просмотров: 295.
