Запишем разложение определителя порядка 3.
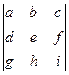 =
= 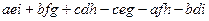 .
.
Вынесем за скобку элементы первой строки (они есть в 2 из 6 слагаемых): 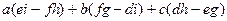 .
.
То, что получилось в скобках, называют алгебраическими дополнениями элементов соответственно 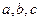 .
.
Выражение в 1-й скобке 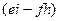 называется алгебраическим дополнением к элементу
называется алгебраическим дополнением к элементу 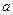 , соответственно
, соответственно
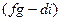 - алгебраическим дополнением к
- алгебраическим дополнением к 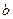 ,
, 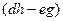 - алгебраическим дополнением к
- алгебраическим дополнением к 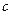 .
.
Заметим, что 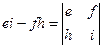 ,
, 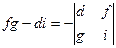 ,
, 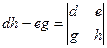 .
.
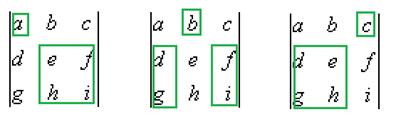
Если для элемента 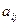 и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу
и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу 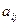 . Всего таких миноров
. Всего таких миноров 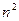 , например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу
, например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу 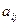 , обозначается
, обозначается 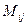 .
.
Мы видим, что в одних случаях алгебраическое дополнение равно минору, а где-то противоположно ему по знаку. Взаимосвязь алгебраических дополнений и миноров для произвольных i,j:
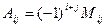 , то есть знаки меняются в шахматном порядке, для верхнего левого элемента
, то есть знаки меняются в шахматном порядке, для верхнего левого элемента 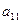 знак «+».
знак «+».
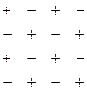
Итак, определители можно вычислять разложением по строке:
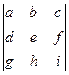 =
= 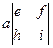
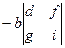
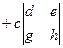 .
.
Разложение возможно по любой строке или по любому столбцу. Так, например, в той же рассмотренной ранее записи можно собрать пары слагаемых, содержащих 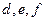 и точно так же вынести за скобку, получится
и точно так же вынести за скобку, получится 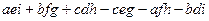 =
= 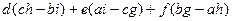 =
=
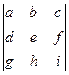 =
= 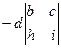
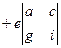
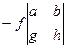 здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.
здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.
Ещё один важный факт! Если матрица треугольная, то 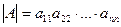 . Докажем этот факт.
. Докажем этот факт.
Пусть дан определитель 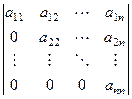 .
.
Если разложить его по первому столбцу, где всего один ненулевой элемент и остальные 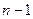 нулей, то сразу переходим к минору меньшего порядка:
нулей, то сразу переходим к минору меньшего порядка:
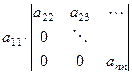 + 0 + ... + 0.
+ 0 + ... + 0.
для него получается аналогичное действие, тогда на следующем шаге получаем 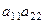 умножаются на определитель треугольной матрицы, у которой угловой элемент
умножаются на определитель треугольной матрицы, у которой угловой элемент 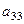 . Продолжая этот процесс, получим
. Продолжая этот процесс, получим 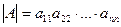 .
.
Задача 24. Вычислить определитель 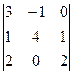 .
.
Решение. Заметим, что 1-й и 3-й столбец содержат очень похожие группы элементов а именно 1 и 2. Вычтем из 1-го столбца 3-й, а затем разложим по 1-му столбцу.
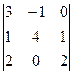 =
= 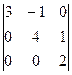 =
= 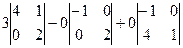 =
=
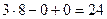 .
.
Ответ. 24.
Задача 25 (а,б). Вычислить определитель 4 порядка двумя способами: а) разложением по 1-й строке. б) с помощью преобразований матрицы.
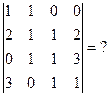
Решение. Первый способ.
Разложение по 1-й строке:
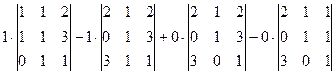
Очевидно, что последние 2 минора 3-го порядка вычислять не надо, так как они умножаются на 0. Осталось вычислить два минора 3 порядка, то есть мы свели определитель 4 порядка к определителям 3 порядка.
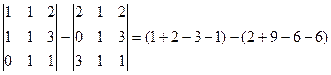 =
= 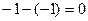 .
.
Ответ. 0.
Второй способ. Из 2-го столбца вычтем 1-й
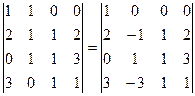
А теперь разложим по 1-й строке, причём реально для вычисления останется только один минор третьего порядка.
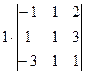 . Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю.
. Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю.
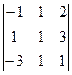 =
= 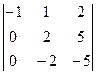 =
= 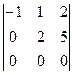 = 0 .
= 0 .
Ответ. 0.
Задача 26. Вычислить определитель 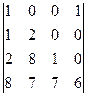 .
.
Решение. Можем разложить по 1-й строке (там всего 2 элемента отличны от 0). Но можно сначала упростить матрицу, а именно, отнять от 4 столбца 1-й столбец. Тогда в 1-й строке будет всего один ненулевой элемент. Также выносим 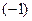 из последнего столбца.
из последнего столбца.
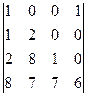 =
= 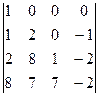 =
= 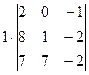 =
= 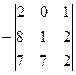 =
=
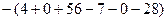 =
= 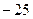 .
.
Ответ. 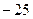 .
.
Задача 27. Вычислить определитель 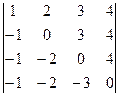 .
.
Решение. Прибавим 1-ю строку ко 2-й, 3-й и 4-й.
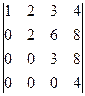 . Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24.
. Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24.
Ответ. 24.
Домашняя Д3. Найти определитель 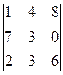 . Ответ.
. Ответ. 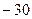 .
.
Домашняя Д-4. Вычислить определитель 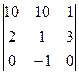 . Ответ. 28.
. Ответ. 28.
Домашняя Д-5. Вычислить определитель 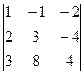 . Ответ. 50.
. Ответ. 50.
Домашняя Д-6. Вычислить определитель 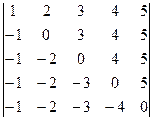 .
.
Ответ. 120.
Практика № 4. Дата 18.09.2018.
Задача 28. Вычислить определитель 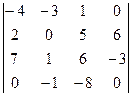 .
.
Решение. Наиболее удобно, если мы хазотим применить метод Гаусса для упрощения матрицы, поставить число 1 в левый верхний угол. Сделаем это, поменяв местами 1 и 3 столбцы.
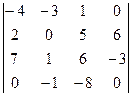 =
= 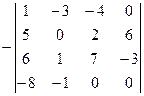
Меняя местами два столбца, долдны домножить на 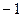 , что и сделано.
, что и сделано.
Но теперь заметим ещё и тот факт, что в 4 стоке только отрицательные числа. Можно вынести коэффициент 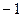 их этой строки, и знак перед всем выражением снова станет + Итак:
их этой строки, и знак перед всем выражением снова станет + Итак:
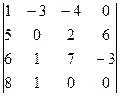
В последней строке всего 2 числа из 4-х отличны от 0. Вычтем из 1-го столбца второй, умноженный на 8, чтобы в последней строке оставить лишь одно число. А потом разложим по последней строке.
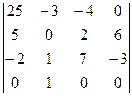 =
= 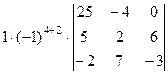 =
= 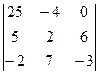
а этот определитель уже вычислим обычным путём, например, допишем копии 1 и 2 столбцов.
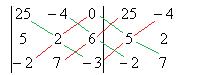
По зелёным линиям умножаем тройки чисел и не меняем знак, а по красным - меняем знак (изучали ранее этот метод).
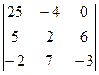 =
= 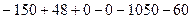 =
= 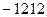 .
.
Ответ. 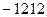 .
.
Обратная матрица.
Формула вычисления элементов обратной матрицы: 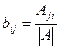 .
.
Алгоритм нахождения 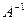 .
.
1. Проверить невырожденность с помощью определителя.
2. Составить матрицу из дополняющих миноров Mij.
3. Изменить знаки в шахматном порядке, то есть домножить на (-1)i+j, где i,j - номера строки и столбца.
4. Транспонировать полученную матрицу.
5. Поделить на определитель исходной матрицы.
Задача 29. Найти обратную матрицу 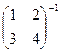 .
.
Решение. 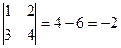 . Вывод:
. Вывод: 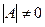 , существует обратная матрица.
, существует обратная матрица.
Матрица из миноров: 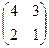 .
.
Матрица из алг. дополнений: 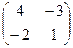 .
.
Транспонируем её: 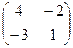 .
.
Делим её на определитель, и записываем ответ: 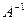 =
= 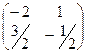 .
.
Можно сделать проверку: 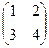
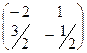 =
= 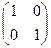 .
.
Ответ. 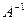 =
= 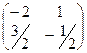 .
.
Задача 30. Найти обратную матрицу для 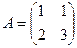 .
.
Решение. 1). Проверяем определитель 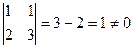 , так что обратная матрица существует.
, так что обратная матрица существует.
2) Составляем матрицу из дополняющих миноров, то есть для каждой клетки вычёркиваем строку и столбец, остаётся подматрица порядка 1, то есть то число, которое напротив, как раз и является дополняющим минором. Получаем 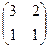 .
.
3) В шахматном порядке меняем знак там, где i+j нечётное.
Тем самым, мы переходим от 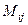 к
к 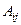 . Получили
. Получили 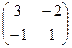 .
.
4) Транспонируем эту матрицу. 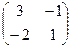 .
.
5) Определитель был равен 1. Делить на 1 не обязательно, можно автоматически считать, что уже и так разделили.
Ответ. 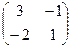 .
.
Проверка: 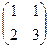
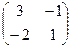 =
= 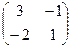
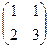 =
= 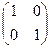 .
.
Минута теории. Докажем, что не существует различных матриц «обратной слева» и «обратной справа». Так как коммутативность в общем случае не выполняется, то вовсе не очевидно, что обратная матрица единственна, можно предположить, что левая обратная и правая обратная - различны. Докажем, что если 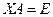 и
и 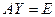 , то
, то 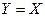 .
.
Доказательство. Пусть 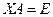 и
и 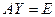 .
.
По закону ассоциативности, можно записать такое равенство: 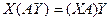 . Но тогда получается
. Но тогда получается 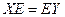 , то есть
, то есть 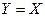 .
.
Перейдём к задачам с матрицами 3 порядка.
Задача 31. Найти обратную матрицу 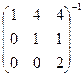 .
.
Решение. Сначала ищем определитель. Так как матрица треугольная, то достаточно перемножить числа по диагонали. 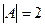 .
.
Строим матрицу, состоящую из дополняющих миноров.
Зачёркиваем ту строку и тот столбец, где находится элемент, и остаётся минор 2 порядка из 4 элементов.
На схеме показано, что именно надо зачеркнуть:
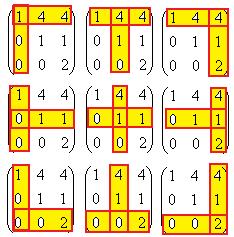
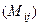 =
= 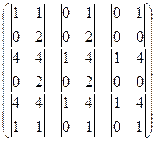 =
= 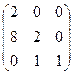 .
.
Теперь надо сменить знаки в шахматном порядке, т.е. переходим от миноров к алгебраическим дополнениям. Обведено красным, где надо менять знак. Ясно, что 0 остаётся 0, там знак менять нет смысла.
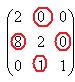
Получили: 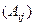 =
= 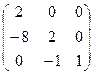 .
.
Транспонируем эту матрицу, то есть бывшие строки запишем по столбцам.
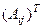 =
= 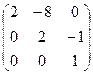 . И осталось разделить на
. И осталось разделить на 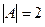 .
.
Ответ. 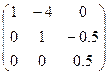 .
.
Задача 32. Найти обратную матрицу 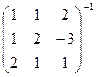 .
.
Решение. Найдём определитель
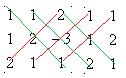
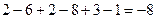 .
.
Найдём матрицу из дополняющих миноров к каждой из 9 клеток.
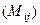 =
= 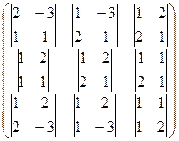 =
= 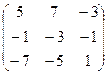 .
.
Меняем знаки в шахматном порядке, то есть там, где i+j нечётное.
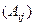 =
= 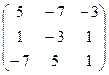 .
.
Затем транспонируем эту матрицу.
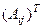 =
= 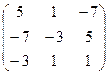 . Осталось только разделить на
. Осталось только разделить на 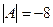 .
.
Ответ. 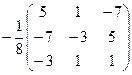 .
.
Задача 33. Найти обратную матрицу 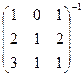 .
.
Решение. Сначала находим определитель.
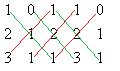
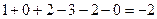 .
.
Найдём матрицу из дополняющих миноров.
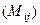 =
= 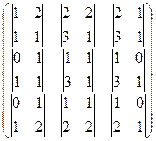 =
= 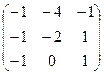 .
.
Меняем знаки в шахматном порядке, там, где i+j нечётное.
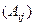 =
= 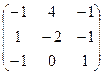 .
.
Затем транспонируем эту матрицу.
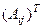 =
= 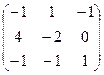 . Затем делим на
. Затем делим на 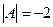 .
.
Ответ. 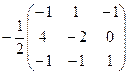 =
= 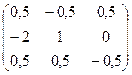 .
.
Задача 34. Матричным методом решить систему уравнений:
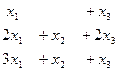
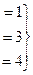
Решение. Запишем систему в виде: 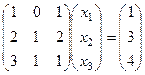 .
.
Обратите внимение, что основная матрица системы это та самая матрица, для которой мы нашли обратную в прошлой задаче.
Если у нас есть равенство 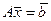 , то
, то 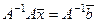 , тогда
, тогда 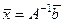 .
.
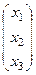 =
= 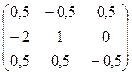
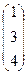 =
= 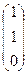 .
.
Ответ. 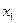 =1,
=1, 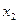 =1,
=1, 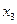 =0.
=0.
Задача 35. Найти обратную матрицу 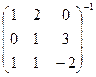 .
.
Решение. Сначала вычислим определитель: 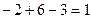 .
.
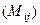 =
= 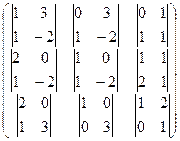 =
= 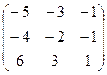 .
.
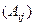 =
= 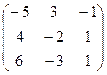 ,
, 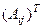 =
= 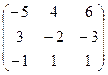 .
.
Исходный определитель был равен 1, так что делить не нужно.
Ответ. 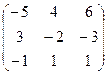 .
.
Дата: 2019-02-02, просмотров: 355.