Задача Д-7. Найти обратную матрицу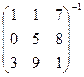 
.
Ответ.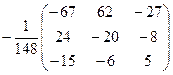 
.
Задача Д-8. Найти обратную матрицу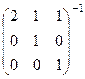 
.
Ответ.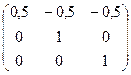 
.
Практика № 5. Дата 25.09.2018.
Матричные уравнения. Пусть А - квадратная матрица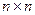 
, 
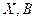- матрицы размера 
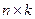(чаще всего в таких задачах 
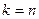, то есть все рассматриваемые матрицы квадратные), причём 
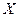- неизвестная матрица. Тогда определено умножение 
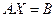. Матрицу 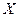таким образом. Домножим всё равенство слева на обратную матрицу 
: 
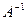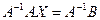. Тогда 
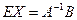, то есть 
.
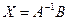Задача 36. Решить матричное уравнение 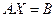, где 
.
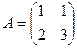
Решение. Требуется найти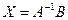 
, заметим, что матрица А тут в точности такая, для которой мы искали обратную в прошлой задаче.
Так, можно использовать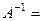 
.
= 
= 
.
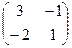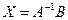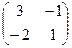
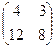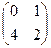Ответ.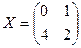 
. Проверка.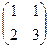 
= .
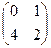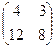Задача Д-9. Решить матричное уравнение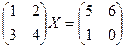 
.
Ответ. 
.
Ранг матрицы.
Для прямоугольных матриц не существует понятие определителя, однако там можно выбирать квадратные подматрицы, и для них определитель вычислить можно. Если задать какие-нибудь k номеров строк и k номеров столбцов, то на пересечениях получится минор из k2 элементов. Он может быть вырожденным либо нет. Существует минор максимального порядка, который является невырожденным. Его порядок и называется рангом матрицы.
Определение. Порядок наибольшего невырожденного минора называется рангом матрицы. Обозначается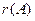 
.
Ранг прямоугольной матрицы размера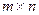 
меньше или равен, чем минимальное из чисел m, n. Причина: минор более высокого порядка в этой матрице просто не существует, ведь размер вписанного квадрата не может превышать ни длину, ни ширину прямоугольника, в который вписан этот квадрат.
Задача 37. Найти ранг матрицы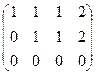 
.
Решение. Здесь есть невырожденный минор порядка 1, это любой ненулевой элемент. Также есть минор порядка 2, например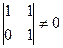 
.
Чтобы выяснить, равен ранг 2 или 3, надо перейти к рассмотрению миноров 3 порядка, причём их можно рассматривать не все, а достаточно только окаймляющие, то есть содержащие уже найденный минор меньшего порядка.
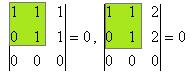
поэтому ранг не равен 3, а остаётся равен 2, так как минор 2 порядка уже найден. Миноров 4 порядка в этой матрице нет, так как всего 3 строки. Итак,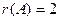 
. Цветом закрашен базисный минор.
Ответ.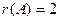 
.
Метод элементарных преобразований для нахождения ранга.
Бывает лучше упростить матрицу, чтобы видеть, какие миноры равны 0 или не равны 0. Как и при вычислении определителей, можно прибавлять к строке другую строку, умноженную на число, то же самое со столбцами. Но при нахождении ранга даже больше возможных действий, чем при вычислении определителя: можно менять местами строки (столбцы), умножать строки (столбцы) на коэффициент. Дело в том, что соответствующие миноры в этом случае меняют знак или умножаются на с, но ведь свойство быть равными 0, либо не равными 0, от этого не меняется!
Если число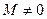 
, то 
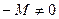и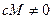 
.
Задача 38. Найти ранг матрицы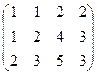 
Решение. Из 2-й строки вычесть 1-ю, а из 3-й удвоенную 1-ю. 
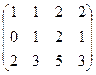
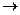
теперь из 3-й строки вычтем 2-ю 
.
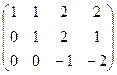Ниже главной диагонали получились нули.
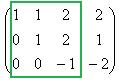
Теперь лучше видно базисный минор порядка 3. Ранг = 3. Если бы оказалось, что последняя строка состоит из нулей, то тогда был бы ответ ранг матрицы = 2.
Ответ. 
.
Задача 39. Найти ранг матрицы.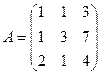 
.
Решение.
Метод 1. Выбираем окаймляющие миноры, начиная от левого верхнего угла. Видно, что минор 2 порядка не равен 0, поэтому ранг больше или равен 2.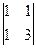 
.
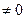Вычисляя минор 3 порядка (а он здесь единственный, это и есть сам определитель матрицы) видим, что он равен 0.
. Тогда ранг не равен 3.
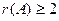, но при этом 
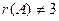. Остаётся единственный вариант: 
.
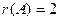Метод 2. Преобразуем матрицу к треугольному виду.
Вычитаем из 2-й строки 1-ю, и из 3-й удвоенную 1-ю.
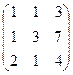
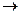
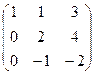
Теперь 2-ю строку, умноженную на 0,5, прибавим к 3-й.
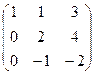
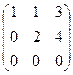
Теперь видно, что 3-я строка состоит из нулей, поэтому ранг не может быть равен 3. Минор 2-го порядка тоже сразу виден, это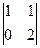 
.
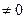Ответ. .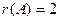
Задача 40. Найти ранг матрицы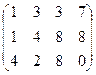 
.
Решение.
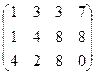
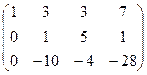
Теперь 2-ю строку, домноженную на 10, прибавим к 3-й.
.
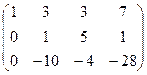
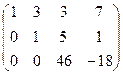Итак, исходная матрица сводится к такой, в которой уже есть треугольная структура в первых трёх столбцах.
Очевидно, что обведённый минор равен 46, не равен 0. Он 3-го порядка, поэтому ранг равен 3.
Ответ: .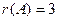
Задача 41. Найти ранг матрицы и базисный минор.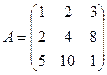 
.
Решение. Преобразуем матрицу:
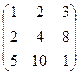
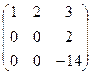
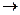
Сначала из 2 строки вычитаем 1-ю, домноженную на 2, то есть вычитаем строку (2 4 6) а из 3-й 1-ю, домноженную на 5, т.е. строку (5 10 15). Затем к 3-й прибавляем 2-ю с коэффициентом 7.
Видно, что базисный минор не может быть в левом верхнем углу, потому что во 2-й строке два нуля. Зато можно найти минор 2 порядка, состоящий из частей 10и 3 столбца, либо 2 и 3-го.
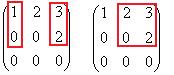
Минор порядка 3, то есть сам определитель всей этой матрицы, равен 0, так как третий столбец содержит только нули. Поэтому ранг равен 2, а не 3.
Ответ. .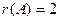
Задача 42. Найти ранг матрицы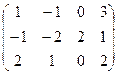 
.
Решение. Преобразуем матрицу. Ко второй строке прибавим 1-ю, а от 3-й отнимем удвоенную 1-ю.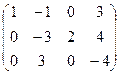 
теперь к третьей прибавим вторую, получим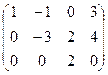 
.
Ранг равен 3, так как есть невырожденный минор 3 порядка.
Ответ.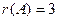 
.
Задача 43 (вариант задачи 42, но с параметром).
Найти параметр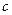 
, при котором ранг матрицы равен 2:
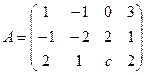
Решение.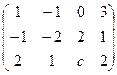 
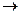
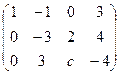
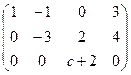
Третья строка состояла бы из всех нулей, только если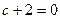 
, то есть 
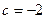. То есть, если бы на месте a33 изначально было число -2, то ранг был бы меньше, так как в итоге получилась бы третья строка из всех нулей.
Ответ.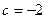 
.
Задача 44. Найти ранг матрицы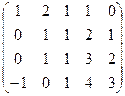 
.
Решение. Преобразуем методом Гаусса к треугольной форме.
.
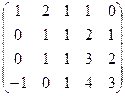
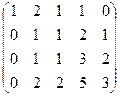
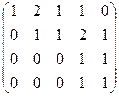
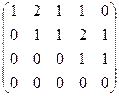Видно, что 4-я строка из нулей, поэтому ранг не равен 4, то есть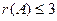 
. Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой:
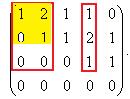
Этот минор невырожденный, и он тоже является окаймляющим (ведь он полностью включает в себя квадрат, закрашенный жёлтым). Мы нашли базисный минор порядка 3. Также можно было рассматривать аналогичное в 1,2,5 столбцах, тоже минор порядка 3.
Ответ. .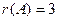
Задача 45. Доказать, что 3 столбец матрицы
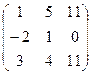
является линейной комбинацией первых двух, и найти коэффициенты этой комбинации.
Решение. Во-первых, если вычислить определитель и обнаружить, что он равен 0, то этим самым уже доказана линейная зависимость столбцов. Однако требуется найти коэффициенты, поэтому запишем систему уравнений:
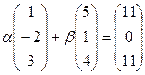
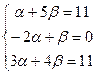
Прибавим удвоенное 1-е уравнение ко 2-му, и вычтем утроенное 1-е из 3-го.
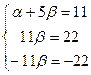отсюда видно, что 
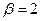, тогда 
.
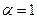Ответ. коэффициенты линейной комбинации равны 1 и 2.
Задача 46. Найти такие параметры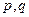 
, что ранг матрицы равен 1:
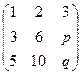
Решение. Преобразуем методом Гаусса к треугольной форме.
.
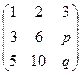
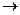
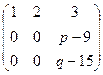Есл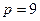и 
и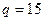 
, то две последних строки только из нулей, и равен будет равен 1.
Ответ.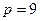 
, 
.
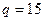Задача 47. Найти ранг матрицы.
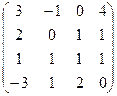
Решение. Для удобства преобразования методом Гаусса, сначала поменяем местами 1 и 3 строки. Ещё можно сразу прибавить 3-ю строку к 4-й.
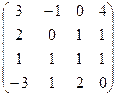
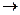
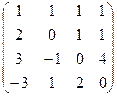
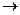
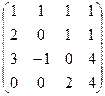
Дальше стандартным методом, обнулим всё ниже угла.
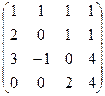
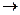
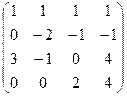
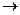
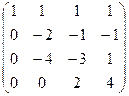
Для удобства вычислений домножим 2 строку на (-1), ранг при этом не меняется. Затем прибавим к 3 строке удвоенную 2-ю.
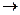
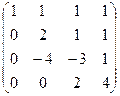
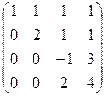
Теперь осталось прибавить к 4 строке удвоенную 3-ю.
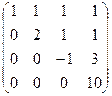. Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому 
.
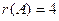Ответ.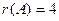 
.
Задача 48. Найти значение параметра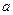 
, при котором ранг матрицы был бы равен 3.
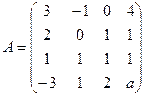
Ответ.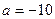 
.
Практика № 6. Дата 28.09.2018.
Системы линейных уравнений.
Теоретический материал.
Обычный, матричный и векторный виды записи системы уравнений:
, 
,
.
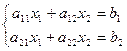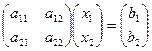Основная (А) и расширенная матрица (С).
, 
.
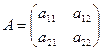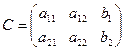Определение. Если существует хотя бы одно решение (то есть набор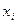 
, обращающий в тождества все уравнения) то система называется совместной, а если решения не существует, то несовместной, или противоречивой.
Слово «совместная» система означает, что уравнения совместны между собой, не противоречат друг другу. Примеры:
Совместная: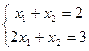 
есть решение (1,1).
Несовместная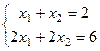 
если вычесть из 2-го уравнения удвоенное первое, получим противоречие: 0=2. А вот если в правой части 2-го уравнения было бы 4, а не 6, то система была бы совместной.
Определение. Если решение системы линейных уравнений единственно, то она называется определённой, если не единственно, то неопределённой.
Определённая: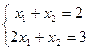 
экв.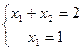 
решение (1,1).
Неопределённая: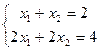 
Решения: (1,1) или (2,0) или (0,2) или (3,-1) или (4,-2), их бесконечно много. Фактически 2-е уравнение лишнее, а из 1-го следует 
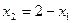. Что бы мы ни подставляли вместо 
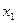, найдётся 
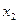. Единственного точного решения как такового здесь нет, их бесконечно много. Запись 
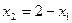здесь называется общим решением, а переменная 
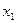, которую перенесли вправо и можем свободно задавать - свободной переменной.
Теорема Кронекера-Капелли о совместности системы уравнений.
Система линейных уравнений совмстна тогда и только тогда, когда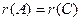 
(ранг основной матрицы равен рангу расширенной матрицы).
Дата: 2019-02-02, просмотров: 223.
