Задача 106.  Построить уравнение плоскости, проходящей через точку А (1,2,3) перпендикулярно вектору 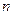(1,4,2)

Решение. Для произвольной точки 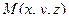 в плоскости, вектор  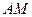с координатами 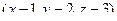ортогонален 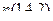. Их скалярное произведение 0. Тогда 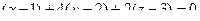, т.е.

.

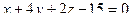Ответ. Уравнение плоскости .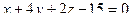

Задача 107.  Построить уравнение плоскости по точке (2,2,8) и перпендикуляру (3,3,7).

Решение. Как и в прошлой задаче, берём произвольную точку 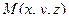 в плоскости, тогда вектор 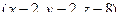ортогонален вектору 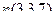. Тогда  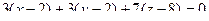из чего следует .

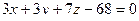Ответ. .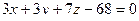

Задача 108.  Построить уравнение плоскости по точке 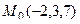 и двум  направляющим векторам 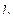(4,2,3) и .

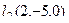Решение. Способ 1. Сначала можно найти нормаль как векторное произведение: 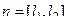, а затем уравнение плоскости по точке и нормали.

 =  = .

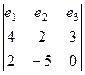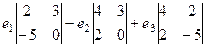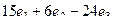Итак, нормаль 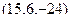, при этом можно заметить, что есть общий множитель 3, и поделить на 3, ведь от изменения длины, направление нормали не изменится. Итак, рассматриваем .

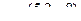Теперь возьмём произвольную точку в этой плоскости, и проведём к ней вектор от точки 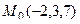. Это вектор 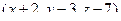. Он ортогонален вектору .

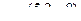Тогда , т.е. .

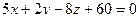Но это было решение в 2 этапа. А можно проще:

Способ 2. Возьмём вектор 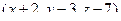 в плоскости, тогда 3 вектора, а именно 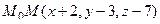, 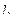(4,2,3) и  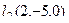должны образовывать линейно-зависимую систему. То есть, можем сразу найти такой определитель и приравнять к 0:

 =  = .

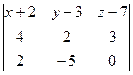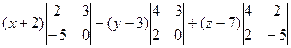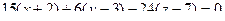Из этого следует 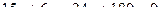. Такое уравнение можно сократить на 3, и получается .

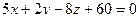Ответ. .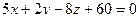

Задача 109.   Построить уравнение плоскости, проходящей через (0,0,0) параллельно 2 направляющим (1,1,2) и (2,1,3).   

Решение. Вектор от начала координат до произвольной точки 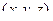, который сам имеет координаты 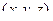, лежит в плоскости двух направляющих, т.е. определитель равен 0.  = .

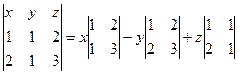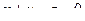Ответ. .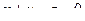

Задача 110.  Построить уравнение плоскости по трём точкам. А(1,2,3), В(3,5,7), С(4,5,6).

Решение. Здесь можно одну из точек, например А, рассматривать в качестве основной, а две другие помогут найти 2 направляющих вектора: АВ и АС. АВ = (2,3,4), АС = (3,3,3).

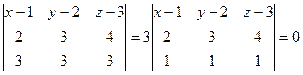
Для удобства вычислений, вынесли из определителя коэффициент 3.

Можно сразу сократить на него правую и левую часть.

Итак,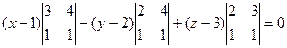   

.  

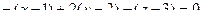
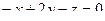Сократим ещё на , получим .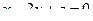

Ответ. .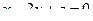

Практика № 12. Дата 26.10.2018.

Задача 111. Найти расстояние от точки M₁ (3,1,5) до плоскости .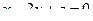    

Решение. По формуле 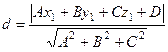 получаем, что

 =  = = .

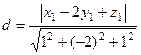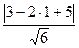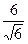Ответ. .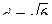

Задача 112. Найти угол между двумя плоскостям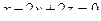и:  и .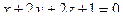 

Решение. Нормали к этим плоскостям: 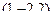 и .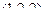 

Нормали не коллинеарны, то есть плоскости не параллельны, значит, они действительно пересекаются по какой-то прямой, и между ними есть какой-то угол.

 =  = .

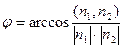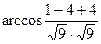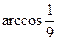Кстати, константа в уравнении одной из плоскостей никак не влияет на ответ, так как параллельный перенос плоскости не влияет на угол, который она образует с другой плоскостью.

Ответ. 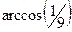, что приблизительно составляет 83,6 градусов.

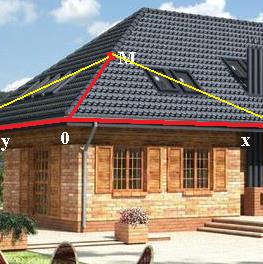
Задача 113. Через точку 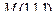 и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти тупой угол между этими плоскостями.

Решение. Если плоскость содержит ось и точку, то в ней по крайней мере содержится начало координат, и 2 такие направляющих: один проведён от (0,0,0) к точке 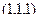, а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.

А затем мы найдём угол между их нормалями. Эти плоскости можно представить так: две наклонные части крыши. Плоскость, перпендикулярная линии ОМ, не горизонтальна, так что угол между двумя частями такой крыши вовсе не 90 градусов. Чем более пологая крыша, тем ближе этот угол к 180, а чем более крутая, тем ближе к 90. Плоскость, перпендикулярная стыковочной линии крыши, а именно линии ОМ, показана жёлтым цветом. 

Строим уравнение 1-й плоскости. Возьмём 3-й вектор, проведённый к какой-то произвольной точке 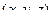 от начала координат. Тогда 3 радиус-вектора, проведённых из начала координат, а именно 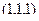, , 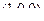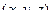должны образовать линейно-зависимую систему.

=  = .

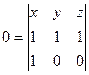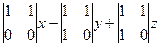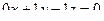Нормаль к этой плоскости .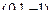

Строим уравнение 2-й плоскости. Аналогично, только (0,1,0).

=  = .

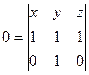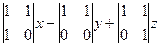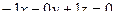Нормаль к этой плоскости .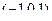

Известно, что .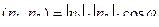

Тогда 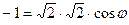, т.е. 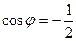, угол 120 градусов. 

Замечание. Если бы надо было найти косинус наименьшего угла, то есть острого, то должны были бы рассматривать модуль 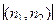, чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.

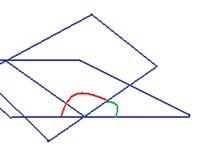
Вообще же, всегда имеется два угла, 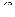 и 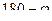. В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как  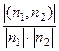либо 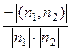. Ответ. .

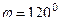Прямая в пространстве