Вводная часть. О влиянии размерности на скорость убывания энергии волн. Землетрясения и цунами. Векторы и действия над ними. Матрицы и их связь с системами векторов.

Действия над матрицами.

Задача 1. Найти сумму и разность матриц: +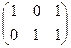

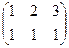
Решение. Складываем поэлементно:

 = .

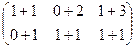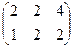Вычитаем:

 = .

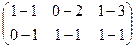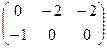Ответ. Сумма: 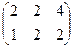 разность: .

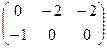Задача 2. Найти сумму матриц: +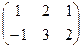

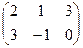
Решение. Складываем поэлементно:

 = .

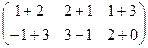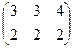Ответ.   .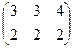

Задача 3. Даны матрицы , .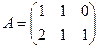 

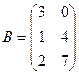Найти 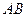 и .

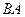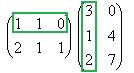
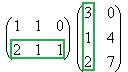
Решение. Запишем эти матрицы. Если первую разбить на строки, а вторую на столбцы, то видно, что есть всего 4 варианта скалярно умножить друг на друга вектор-строку их первой на вектор-столбец из второй.

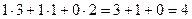
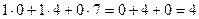
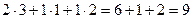
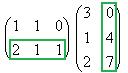
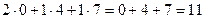
Например, если умножаем строку номер 1 на столбец номер 2, то и число, которое при этом получается, ставим в 1 строку 2 столбец новой матрицы. Итак,

 = .    

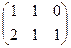
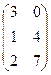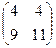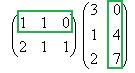
Теперь найдём 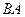. В данном случае первую матрицу можно разрезать на 3 строки, а вторую на 3 столбца. Таким образом, получаем 9 чисел.

Покажем, например, как 1-я строка скалярно умножается на 1-й столбец, они обведены. .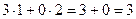

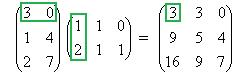
Ответ. .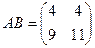   

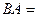
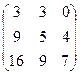Задача 4. Найти произведения матриц:

, , .

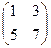
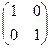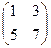
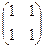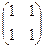
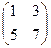Решение.

 =  =  = .

 =  =  = .

 =  =  = .

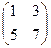
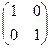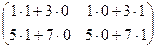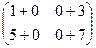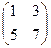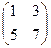
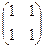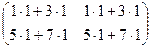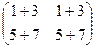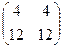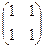
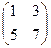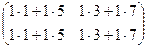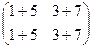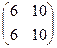Ответ. , , .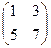

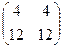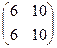Примечания.

1) Видим, что в общем случае может не выполняться закон коммутативности при умножении матриц, то есть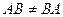

 2) При умножении на матрицу, состоящую из всех единиц, исходная не получается, а вот если единицы по диагонали - получается. Матрица 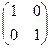 называется единичной матрицей. При этом выполняется .

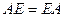Задача 5. Дана матрица 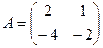 найти .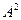

Решение. Умножим матрицу саму на себя, то есть две её копии напишем рядом и умножим их.

 =  =

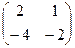
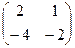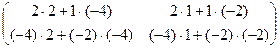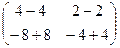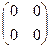 = .  Ответ. .

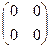Как видно из этого примера, для матриц, в отличие от чисел, возможно, что получается нулевой объект в ответе, притом что в исходной матрице вообще ни одного нуля не было. Это из-за особенностей её строения: правый столбец в 2 раза меньше, чем левый, а нижняя строка в минус 2 раза больше, чем верхняя. И вообще, если взять пару матриц, где у первой будет пропорциональность строк (в k раз больше) а у второй - столбцов (в минус k раз меньше) получим такой же эффект.

Задача 6. Найти произведение матриц .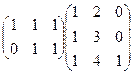

Решение. Размеры согласованы: длина строки 1-й матрицы равна высоте столбца 2-й матрицы. Первую можно мысленно разрезать на 2 строки, вторую на 3 столбца. Итого будет 6 различных произведений строк на столбцы.

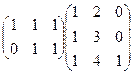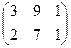 = . Ответ. .

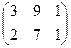Задача 7. Вычислить  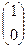и .

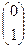Заметим, что получаются 1-й и 2-й столбец матрицы.

= , = .

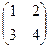
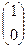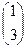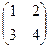
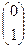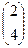Квадратная матрица отображает вектор в вектор. Коротко о понятии линейного оператора и строении его матрицы и о том, что при умножении на i-й базисный вектор получается столбец номер i.