В данном разделе (т.е. в разделе 2), как следует из его названия (см. стр. 61), рассматриваются растворы неэлектролитов. Однако чтобы не возвращаться еще раз к коллигативным свойствам, обратимся в этом пункте к растворам электролитов.
1. В случае электролитов в формулах для коллигативных свойств (п. 8.9)
поправку на особенности реальных растворов делают не путем замены концентраций на активности, а путем введения изотонического коэффициента i :
 |
2. Для сильных электролитов этот коэффициент равен
 |
где γ — коэффициент активности, а mи — количество ионов, на которое
распадается электролит. Два примера расчета изотонического коэффициента
по формуле (8.42) приведены в табл. 8.3.
3. а) В случае же слабых электролитов отличие ί от mи обусловлено, главным образом, неполной диссоциацией (а не взаимодействием диссоциирующих
частиц). Поэтому коэффициент активности можно считать равным 1, и вся
задача состоит в расчете среднего числа частиц, образующихся из одной молекулы.
б) Используя степень диссоциации α, можно записать:
 |
откуда
в) Последняя формула используется тогда, когда изотонический коэффициент
определен экспериментально (например, по изменению температуры замерзания раствора, т.е. по формуле (8.41,в)). В этом случае, как видно, можно вычислить степень диссоциации слабого электролита.
8.13. Растворение газов в жидкости (законы Генри и Сеченова)
Опять обратимся к растворам неэлектролитов. Некоторые особенности
имеет растворение газов.
1. а) В отличие от твердых тел, здесь растворяемое вещество тоже (как и растворитель) является летучим, поэтому можно рассматривать фазовое равновесие в системе раствор — газ над раствором.
б) Для идеального раствора к этому равновесию тоже применим закон Рауля (8.12), который в данном случае следует записать так:
 |
Следовательно, давление газа над раствором (как и любого летучего компонента раствора) пропорционально молярной доле газа в растворе. Здесь
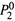— предел, к которому стремится давление газа над раствором при X2 → 1.
 |
в) Однако для реальных систем вместо
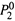пишут эмпирическую константу Генри:
2. а) Нередко это соотношение рассматривают в обратную сторону:
 |
б) Перейдем к молярной концентрации:
 |
Тогда получаем:
 |
где Kp— константа растворимости, которую можно представить в виде:
в) Тем самым выведен закон Генри: концентрация растворенного в жидкости газа пропорциональна парциальному давлению этого газа над раствором.
3. Уточним природу константы растворимости. (Сейчас она определена лишь
через другую эмпирическую константу — Kг.)
 |
а) Запишем условие равенства химических потенциалов газа в растворе и над ним:
в котором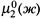 
— химический потенциал растворенного газа при его единичной молярной концентрации, а 
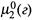— потенциал газа над раствором при его единичном парциальном давлении.
б) Обозначим:
 |
Тогда находим:
 |
в) Отсюда следует температурная зависимость Kp— такая же, как для константы равновесия химической реакции (п. 5.9):
г) Если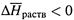 
(растворение газа — экзотермический процесс), то с ростом температуры K p уменьшается, и растворимость газа снижается.
Данное явление весьма характерно для газов.
4. На растворимость газов влияют и соли, присутствующие в растворе. Это
устанавливается эмпирическим законом Сеченова:
 |
Дата: 2019-02-02, просмотров: 232.
