Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1. В итоге, с законом Рауля связаны 4 явления, касающиеся влияния растворенного вещества на свойства раствора. Это

a ) понижение давления насыщенного пара растворителя: ΔР₁ /P⁰₁ = Х₂ , (8.17, в)

б) понижение температуры замерзания раствора: ΔТ_к = K_эб b₂ ,                (8.20)

в) повышение температуры кипения: ΔT_з = – К_з b₂,                                    (8.21)

  г) наличие осмотического давления: П ≈ с₂RT .                                        (8.28)

2. Все эти явления объединяют в группу так называемых коллигативных свойств растворов.

а) Термин означает, что выраженность данных свойств зависит только от
количества частиц растворенного вещества в единице объема и не зависит от
их природы.

б) Однако такое утверждение (равно как и выписанные соотношения) спра-
ведливо только для идеальных растворов. В случае же неидеальных растворов
имеет значение и природа растворенного вещества.

 

Активности веществ

 

В вышеприведенных выражениях для коллигативных свойств растворов
фигурируют концентрации растворенных веществ. Использовались концентра-
ции и тогда, когда записывались формулы для константы равновесия, энергии
Гиббса химической реакции, химического потенциала, например:

 

1. а) Но на самом деле, как уже отмечалось для химического потенциала (6.9, б), во всех этих формулах следует писать не просто концентрации, а так называемые эффективные концентрации, или активности веществ. Последние связаны с обычными концентрациями с помощью коэффициентов активности:

причем индексы ( X , с, b ) в обозначениях активности обычно не пишут. Так что под активностью иногда понимают эффективную молярную долю, в других случаях — эффективную молярную концентрацию, а в третьих — эффективную моляльную концентрацию.

б) С учетом сделанного замечания дадим определение. Активность вещества в растворе — это концентрация идеального раствора, которая требуется для проявления точно таких же коллигативных, химических и прочих свойств, как у данного реального раствора.

в) Следовательно, чтобы на практике определить коэффициент активности, необходимо измерить какое-либо свойство раствора, по соответствующей формуле рассчитать эффективную концентрацию и сравнить последнюю с истинной концентрацией.

2. Пример. Пусть для раствора вещества с c₂ = 0,1 М измерили осмотическое давление и по формуле Вант-Гоффа нашли, что такое же давление создает идеальный раствор с концентрацией

Тогда коэффициент активности равен

 

3. При очень низких концентрациях вещества коэффициент активности близок к 1,0 (рис.8.6); при повышении концентрации он снижается (становясь много меньше 1,0); при еще большем увеличении концентрации начинает повышаться и порой даже становится больше 1,0. Некоторые значения коэффициента активности для СаСl₂ приведены в табл. 8.2.

 4. Почему активность обычно отличается от концентрации?

Все дело во взаимодействии частиц вещества друг с другом. Например, ионы K⁺ и Cl^–, на которые распадается в растворе KCl, создают друг вокруг друга многочисленные ионные оболочки. Поэтому некоторая доля частиц как бы выключается из взаимодействия с растворителем и другими компонентами раствора.

5. Итак, в выражениях, где до сих пор писались концентрации, на самом деле
надо писать активности, например:

                                       μ_i   = μ⁰_i + RT ln (γ _i X _i) ,                                               (8.35,а)

 

                                                (a_C)^c (a_D)^d      

          ΔG_рц = ΔG⁰_рц + RT ln –––––––––– = ΔG⁰_рц + RT ln П_а  .         (8.35,б)       

                                                (a_A)^a (a_B)^b         

 

 

Уравнение Гиббса-Дюгема

1. В физической химии известно так называемое уравнение Гиббса-Дюгема.
Оно имеет весьма общий смысл, но с его помощью, в частности, можно
связать коэффициенты активности компонентов раствора. Вывод уравнения таков.

а) Полная энергия Гиббса системы выражается через химические потенциалы компонентов:

откуда

 

б) С другой стороны, известно выражение:

 

в) Сопоставление дает:

или, при постоянных давлении и температуре,

 

2. а) Это и есть уравнение Гиббса-Дюгема, записанное для химических потенциалов. В данной записи оно означает, что для компонентов раствора изменения химических потенциалов взаимосвязаны. Например, увеличение потенциала одного компонента может происходить только за счет уменьшения потенциала другого компонента.

б) Так, увеличение концентрации растворенного вещества повышает его химический потенциал. Но в результате снижается молярная доля растворителя — значит, уменьшается его химический потенциал.

3. а) Подставим в (8.37, б) формулу (8.35, а) и поделим все на ∑ n_i:

 

б) Для двухкомпонентной системы нетрудно убедиться, что второе слагаемое
уравнения (8.38) равно нулю:

 

в) Поэтому первый член уравнения (8.38) тоже равен нулю, и это для двукомпонентной системы можно записать так:

 

4. Вывод таков. Если с ростом X ₂ уменьшается коэффициент активности растворяемого вещества 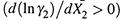, то одновременно увеличивается коэффициент активности растворителя 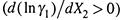. И наоборот. Зная, как уменьшается  γ₂, можно рассчитать и увеличение γ₁.