Для выяснения физического смысла рис. 7.2 подробней остановимся на ее
разделительных линиях и точке их пересечения.

1. а)Линия ОС соответствует ситуации, когда внешнее давление Р (со стороны поршня) совпадает с давлением насыщенного пара над жидкой водой:

б) С увеличением температуры, как известно, давление насыщенного пара
возрастает. Так что линия ОС – это фактически график зависимости давления насыщенного пара над жидкой водой от температуры:

в) Рассмотрим вариант с фиксированной температурой — например, t₁.

I . Пусть 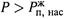: давление поршня больше давления насыщенного пара, и фигуративная точка лежит выше кривой ОС. В таком случае пар образовываться не может — просто потому, что его давления недостаточно, чтобы приподнять
поршень и занять какой-то объем. Вся вода находится в жидком состоянии.

II . Если 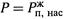 (точка лежит на кривой ОС), то пар уже может обратимо поднимать поршень и создавать газовую фазу, т.е. две фазы находятся в равновесии друг с другом, что соответствует состоянию кипения.

III . Если же 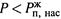 (точка — под кривой ОС), то внешнее давление так мало, что поршень неудержимо поднимается вверх и вся вода превращается в пар, расширяющийся до давления Р. Система опять становится однородной.

г) Итак, кривая ОС описывает зависимость (7.2,б). Но из только что изложенного следует, что эта кривая определяет еще одну зависимость
— температуры кипения от внешнего давления:

                                                 T_к = f ^--1 (P_ex).                                          (7.2,в)

2. Линия ОА . а) При температурах ниже нуля вода находится уже не в жидком, а в твердом состоянии (лед, снег). Но и лед тоже способен испаряться, минуя жидкое состояние.

Переход вещества из твердого состояния сразу в газообразное называется
сублимацией, или возгонкой. Для воды это возможно, что подтверждает простой
пример. Так, мокрое белье, вывешенное на мороз, вначале затвердевает (вода
переходит в твердое состояние), а затем постепенно сохнет. Это-то высыхание
и есть ни что иное, как возгонка воды.

б) Так вот, на линии ОА внешнее давление Р совпадает с давлением насы-
щенного пара надо льдом. Это давление вновь зависит от температуры; следовательно, линия ОА — это зависимость вида

в) В отношении точек, прилегающих к линии ОА, можно провести рассмотрение, как в случае линии  ОС:

- выше линии ОА  внешнее давление не позволяет образовываться газовой фазе – имеется только твёрдая фаза;

- на линии ОА  существует обратимое равновесие между твёрдой и газообразной фазами;

- а ниже этой линии, из-за малости внешнего давления, вся вода из твёрдой фазы возгоняется в газообразную.

3. а)Линия ОВ отражает равновесие в системе лед - вода. Как известно, при
атмосферном давлении плавление льда происходит при 0°С. Это точка К на
линии ОВ.

б) Однако температура плавления льда, хотя и очень слабо, зависит
от внешнего давления в системе:

                                                  Т_пл = Ψ(Р)                                               (7.4)      

А именно: при резком уменьшении давления Т_пл немного увеличивается,
что является одним из проявлений принципа Ле Шателье (п. 6.4).

II . Действительно, согласно этому принципу, понижение давления должно
сдвигать равновесие процесса

                        Состояние 1 (лёд) 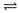 Состояние 2 (вода)                      (7.5)

в сторону состояния с бóльшим объемом (что отчасти компенсирует снижение внешнего давления).

III . Как известно, объём льда больше объёма воды аналогичной массы (при t ≈ 0 ^o C ). Следовательно, при уменьшении давления (ΔP < 0) равновесие сдвигается в сторону льда. Поэтому для перехода льда в воду требуется более высокая (чем при прежнем давлении) температура (ΔT_пл > 0). Значит, изменения ΔP и ΔT_пл противоположны по знаку. Наклон кривой ΔT_пл(P) — отрицательный.

в) Таким образом, кривая ОВ отличается по своему характеру от кривой АО:
она (ОВ) отражает не зависимость Р от Т (давления насыщенного пара от
температуры), а, наоборот, зависимость Т от Р (температуры плавления от
давления).

Кривая же ОС, напомним, описывает обе зависимости: 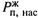от Т и T_к от P_ex.

г) Если фигуративная точка лежит левее кривой ОВ, то вся вода находится в виде льда, а если правее — вся вода в жидком состоянии.

4. Точка О. Допустим, что, оставаясь на кривой ОВ (где твердая и жидкая
фаза находятся в равновесии), мы сильно снижаем внешнее давление — до
того момента, пока оно не сравняется с давлением насыщенного пара надо
льдом и над водой. Тогда появится возможность для образования и третьей
фазы: пар сможет приподнять поршень и создать свою фазу.

Данное состояние и описывается тройной точкой О. Ее координаты:

Таким образом, диаграмма состояния воды (рис. 7.2) рассмотрена не только
с формальной (исходя из правила фаз Гиббса), но и с физической стороны.
Приведем еще один пример однокомпонентных систем.

Диаграмма состояния серы

1. а) У твердой серы (см. п. 7.1) имеются две модификации — ромбическая
и моноклинная. В природе обычно встречается ромбическая форма, при на-
гревании выше T_пер = 95,4° С (при нормальном давлении) постепенно превра-
щающаяся в моноклинную. При охлаждении происходит обратный переход.
Такие обратимые превращения модификаций называются энантиотропными.

б) Итак, при указанной температуре обе формы находятся в равновесии:

причем переход в прямом направлении сопровождается увеличением объема. Естественно, что, по принципу Ле Шателье, температура перехода (T_пер) зависит от давления. Повышение давления (ΔP > 0)  будет сдвигать равновесие в сторону с меньшим объемом (S_ромб), так что для перехода в S_мон потребуется бόльшая температура T_пер (ΔT_пер> 0).

в) Таким образом, здесь знаки ΔP и ΔT_пер совпадают: наклон кривой T_пер(P) — положительный. На диаграмме состояния (рис. 7.3) эта зависимость отражена почти прямой линией АВ.

2. а) Всего же фаз у серы — 4: две названные твердые, а также жидкая и газообразная. Поэтому на диаграмме состояния — 4 области, соответствующие этим фазам. А разделяются фазы шестью линиями, которые соответствуют шести видам фазовых равновесий:

б) Без подробного рассмотрения всех этих областей и линий коротко укажем для них следствия из правила фаз (практически такие же, как для воды):

I. в каждой из 4-х областей – состояние бивариантное:

        Ф = 1  и С = 3 – 1 = 2 ,             (7.9,а-б)        

II . а на каждой из 6-ти линий – состояние моновариантное:

                                   Ф = 2 и С = 3 – 2 = 1 .                               (7.10,а-б)        

III . Кроме того, имеются сразу 3 тройные точки (А, В, С), для которых

                                    Ф = 3 и С = 3 – 3 = 0 .                                  (7.11,а-б)

В каждой из них, как в тройной точке диаграммы воды, существуют одновременно три фазы, и подобные состояния – инвариантны, т.е. нельзя изменить ни одного параметра (ни температуры, ни давления), чтобы не «потерять» хотя бы одну из фаз.