1. Исходные условия. а) Будем также считать, что жидкости
I. неограниченно растворимы друг в друге и
II. обе являются летучими, т. е. дают над раствором пар.
б) Введём обозначения: 1 — менее летучая жидкость, 2 — более летучая, т.е. у первой жидкости — ниже давление насыщенного пара над чистым веществом и, соответственно, выше температура кипения:
 |
в) Вспомним также условие идеальности раствора, согласно которому все виды межмолекулярных взаимодействий в системе — 1–1, 2–2 и 1–2 — одинаковы
по характеру и силе. Примерами являются смеси близких по природе жидкостей: бензол–толуол, гексан–гептан, метанол–этанол.
2. а) Для идеальной смеси закон Рауля (8.12) применим к обоим летучим компонентам:
 |
откуда
б) Получается, что общее давление пара над смесью линейно зависит от состава смеси. Это изображено на рис. 9.1, где
- по оси абсцисс отложена молярная доля в жидкой фазе более летучего компонента,
- пунктирными линиями показаны парциальные давления паров каждого из двух
компонентов (при разном составе смеси)
- и сплошной линией — общее давление
пара над раствором.
3. а) Нетрудно определить состав пара при том или ином составе жидкой фазы. Молярные доли каждого вещества в паре обозначим штрихом. Тогда, например, доля в паре второго компонента такова:
 |
Последнее выражение получено путем деления числителя и знаменателя на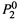 
, а ζ1— величина, меньшая единицы:
поскольку, в соответствии с условием, первый компонент является менее летучим.
 |
б) Заметим: так как X1 + X 2 = 1, то знаменатель выражения (9.4, в) меньше единицы:
в) Таким образом, доля второго (более летучего) компонента в паре выше, чем в жидкой смеси. В этом заключается первый закон Коновалова: по сравнению с жидкой фазой, состав газовой фазы обогащен более летучим компонентом.
На рис. 9.2 это выражается в том, что кривая зависимости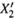 
от X2 идет выше диагонали единичного квадрата. График же данной зависимости нетрудно построить, используя формулу (9.4, в).
Идеальные смеси:
полный вариант диаграммы давления
1. а) Нередко на диаграмме давления (рис. 9.3), кроме зависимости P0 от состава жидкости X2 (линии ж), изображают также линию, связывающую P0
с составом газовой фазы 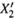(линия п). Для этого удобно ввести еще одну
координатную ось —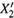 
(хотя часто обходятся и без неё).
б) Тогда построение таково (см. рис. 9.3). Для произвольного значения X2,М по формулам (9.4) рассчитывают соответствующее значение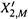 
(большее X2,М) и находят точку пересечения этой ординаты 
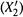с изобарой, проходящей через точку М. Тем самым получают точку М', принадлежащую линии п.
2. Линиями ж и п диаграмма разделяется на три области.
а) Над линией ж система имеет только жидкую фазу (имеется в виду, что система находится под поршнем). В любой точке этой области внешнее давление (создаваемое поршнем) больше возможного давления пара смеси, так что пар не образуется.
б) Между линиями возможно существование двух фаз: и жидкой, и газообразной. Например, в точке О (состав — X2,0, внешнее давление — P0 = Pм) сосуществуют жидкая фаза с составом X2,М и газовая с составом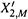 
.
в) А под линией n система имеет только одну газовую фазу.
3. Отметим также, что состав газовой фазы зависит от температуры {закон
Вревского). Это следует из формулы (9.4,в). В ней фигурирует ζ1 — отношение
величин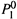 
и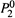 
. Если эти величины с ростом температуры изменяются
непропорционально, то 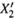оказывается функцией температуры.
Дата: 2019-02-02, просмотров: 267.
