Пусть одна из фаз является газообразной, т.е. в случае, например, диаграммы состояния воды (рис. 7.2) речь идет о кривых ОС и ОА.
 |
1. а) Из уравнения (7.16) получаем следующие формы уравнения Клаузиуса-Клайперона:
Во втором случае энтропия фазового перехода выражена через теплоту этого перехода (см. (7.14,6)).
б) Учтем знаки величин для переходов т → г и ж→ г:
 |
Действительно,
- мольный объем пара всегда значительно больше, чем объем того же вещества в твердом или жидком состоянии (первое неравенство);
- при испарении теплота поглощается веществом (второе неравенство).
 |
в) В итоге, для рассматриваемых фазовых равновесий
т. е. наклон кривой Р(Т) — положительный. Это имелось во всех случаях на диаграммах состояния воды и серы.
2. а) Более того, можно найти и конкретную зависимость давления насыщенного пара (Pп,нас) от температуры. Для этого в разности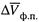 
следует пренебречь объемом вещества в твердом или жидком состояниях, а для удельного (мольного) объема пара использовать уравнение Клайперона—Менделеева:
 |
 |
Подставляем (7.20) в (7.17,6):
б) Примечательно, что последнее уравнение совпадает по форме с уравнением изобары реакции — зависимостью Kp (константы равновесия) от температуры (5.20). Поэтому близки и другие выражения этих зависимостей.
3. а) Так, для небольших интервалов температуры величину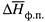 
считают постоянной (хотя на самом деле теплота испарения довольно существенно
зависит от температуры). При таком допущении можно проинтегрировать уравнение (7.21,6), введя постоянную интегрирования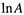 
.
 |
С учетом этого имеем:
б) Формула (7.22,6) подобна уравнению (5.16) и аналогично ему означает ли-
нейную зависимость логарифма соответствующей величины (здесь — давления
насыщенного пара Р) от обратной температуры.
в) На графике этой зависимости (рис. 7.4)
 |
4. а) Если записать (7.22,б) для двух температур и вычесть одно уравнение из другого, придём к формуле, сходной с (5.19) и используемой в практических расчётах:
б) Эта формула (при условии, что известны теплота фазового перехода (Δ H ф.п.) и давление насыщенного пара при температуре T 1) позволяет оценить давление пара при какой-то другой, не очень далеко отстоящей, температуре.
в) Если же температурный интервал широк. его следует разбить на такие достаточно небольшие отрезки, для которых известны средние значения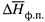 
. После этого можно воспользоваться формулой (7.24) отдельно для каждого отрезка.
 |
5. Наконец, чтобы найти зависимость температуры кипения от внешнего
давления, очевидно, надо решить уравнение (7.22, б) «в обратную сторону»: считая Р известным (и равным внешнему давлению), выразить T = Tk из указанного уравнения:
Дата: 2019-02-02, просмотров: 240.
