1. а) Итак, для идеальной смеси двух жидкостей общее давление пара линейно зависит от молярной доли компонентов:
 |
но для реальных растворов зависимость часто отклоняется от линейной.
б) На диаграмме рис. 9.5 показано: могут быть как положительные отклонения, когда общее давление пара P0 больше того, что ожидается по формуле (9.3)), так и отрицательные отклонения (P0 меньше ожидаемого значения).
 |
в) Эти ситуации суммированы в табл. 9.1.
2. В частности, для смесей с положительным отклонением из данной таблицы видно следующее.
а) В этих смесях энергия взаимодействия между молекулами разных компонентов (E12) меньше, чем, в среднем, между одинаковыми молекулами. Следовательно, при образовании таких смесей энергия межмолекулярных взаимодействий, приходящаяся на одну частицу, уменьшается и молекулы становятся более подвижными.
 |
б) В силу этого образование смесей идет с поглощением теплоты (при условии постоянства температуры):
 |
в) Испаряются молекулы из смеси в таком случае легче, чем из чистых жидкостей: теплота испарения снижается —
г) В результате парциальное давление пара компонента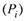 
выше, чем в случае идеальной смеси 
.
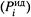3. а) Можно дать еще одну интерпретацию положительного отклонения. В п. 8.5 выведен закон Рауля для идеальных растворов. В случае неидеальных раство-
ров или смесей можно повторить тот же вывод, но коэффициент распреде-
ления вещества между фазами записать не через концентрации, как в (8.14),
а через активности:
 |
б) Тогда, вместо
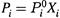, мы придем к выражению
 |
где величина
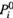(давление пара над чистым компонентом) по-прежнему выражается формулой (8.16):
в) Из (9.12,а) и вытекает объяснение положительного отклонения через активности:
 |
Следовательно, данный тип отклонения наблюдается тогда, когда коэффи-
циенты активности компонентов в жидкой фазе выше, чем в газовой фазе.
4. а) Обе диаграммы давления и кипения при положительном отклонении показаны на рис. 9.6,а–б. В частности, температура кипения смеси при любом её составе (кроме крайних случаев) оказывается ниже, чем для идеальной смеси. Поэтому обе кривые на диаграмме рис. 9.6,б (ж, зависимость Tк от X2, и n, связь 
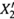с Tк) как бы прогнуты вниз.
б) Для смесей же с отрицательным отклонением диаграммы выглядят, как показано на рис. 9.7,а–б.
в) Еще раз заметим, что на диаграммах давления линия ж всегда идет выше, чем линия n, а на диаграммах кипения — ниже.
г) При наличии того или иного отклонения от идеальности диаграммы строят
только по экспериментальным данным. Теоретический расчет с использованием выкладок (9.7 и 9.12) затруднен из-за того, что аналитическая зависимость коэффициентов активности от концентраций обычно не известна.
Азеотропные смеси
1. На рис. 9.2 мы приводили зависимость состава насыщенного пара (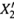 
) от
состава жидкой смеси (X2). Кривая этой зависимости идет с одной стороны от диагонали единичного квадрата, т.е. при любом составе смеси компонент 2 является более летучим, чем компонент 1. Это справедливо и для идеальных, и для многих реальных смесей.
2. Но существуют так называемые азеотропные
смеси, у которых график подобной зависимости в какой-то точке (X2,аз) пересекает диагональ квадрата (рис. 9.8). Это означает, что
- до указанной точки компонент 2 — более летучий (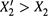 
),
- после нее — менее летучий, а его содержание в паре становится меньше, чем в жидкости ( 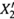< X2).
В самой же азеотропной точке летучесть обоих компонентов совершенно одинакова — состав пара совпадает с составом жидкой фазы.
3. Диаграммы давления и кипения для азеотропных смесей имеют характерный вид. Приведем их вначале для случая, показанного на рис. 9.8, т.е. для ситуации, когда при переходе через точку X2,аз вещество 2 из более летучего становится менее летучим.
 |
а) На диаграмме давления (рис. 9.9,а) для кривой ж мы получаем не просто
положительное отклонение от линейной зависимости (как на рис. 9.5), а и
наличие максимума в точке X2,аз .
I. Действительно, до этой точки компонент 2 — более летучий, отчего увеличение его содержания в жидкой смеси (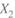 
) повышает общее давление пара над ней.
II . После точки X2,аз данный компонент — уже менее летучий, и дальнейшее увеличение его относительного содержания в жидкой фазе теперь понижает общее давление пара.
III . А поскольку в точке X2,аз состав пара и жидкости совпадает, кривая п должна в этой точке сходиться с кривой ж. Отсюда на диаграмме — как бы две петли.
б) На диаграмме же температур кипения (рис. 9.9,6), соответственно, наблюдается минимум для кривой ж в азеотропной точке. Т. е. здесь — самая низкая температура кипения смеси. Линия п образует две дуги над линией ж.
4. Реже встречаются азеотропные смеси с отрицательным отклонением. Они характеризуются минимумом на диаграмме давления и максимумом на диаграмме кипения (рис. 9.10).
а) Заметим, что, подобно предыдущему случаю, линии ж на обеих диаграммах являются гладкими, т.е. не имеют в точке экстремума разрыва производной, как нередко их изображают.
б) Линии же n находятся с выпуклой стороны линий ж, но при этом не могут заходить за экстремальные значения Р и Tk.
5. а) Однако каким бы ни был тип отклонения азеотропных смесей, им присуще уже известное нам свойство: в точках экстремума на диаграммах давления и кипения составы жидкой и газовой фаз смеси одинаковы.
Это утверждение обозначается как второй закон Коновалова. (Первый закон Коновалова был сформулирован в п.9.1.)
 |
б) Классический пример азеотропной смеси с положительным отклонением — смесь H2O–спирт. Для данной системы азеотропная точка (массовая доля спирта) такова:
в) Примеры азеотропных смесей с отрицательным отклонением — водные растворы HCl и HNO3
Дата: 2019-02-02, просмотров: 233.
