1) Убедиться, что переменные X и Y распределены нормально (или их распределение близко к нормальному).
2) Расположить исходные данные в виде таблицы. В первом столбце указана нумерация, во втором и третьем – числовые значения переменных X и Y.
3) По каждой переменной подсчитываются суммы значений и среднее арифметическое. Находится модуль разности средних значений.
4) Вычисляются по каждой переменной отклонения от среднего и записываются в 4-ом и 5-ом столбцах. Проверяется правильность вычисления (сумма отклонений от среднего должна равняться нулю).
5) Вычисляются квадраты отклонений от среднего и записываются в 6-ом и 7-ом столбцах.
6) Находятся суммы квадратов отклонений по каждой переменной.
7) Подсчитывается значение величины Sd по формуле:
Sd= 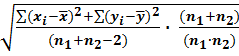
8) Вычисляем t-критерий Стьюдента по формуле:
t эмп = 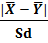
9) Рассчитываем число степеней свободы:
k = n 1 + n 2 – 2
10) По Таблице 9 приложения находятся критические значения t критерия для данного k, соответствующие уровням значимости 0,05; 0,01 и 0,001.
11) Строится ось значимости, наносятся критические и эмпирическое значения критерия. Определяется зона попадания tэмп.
12) Формулируются выводы.
Пример 9.1. Психолог проверял время сложной сенсомоторной реакции выбора (в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, не занимающихся спортом активно. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.
Решение: Результаты эксперимента представлены в виде таблицы.
| № | ||
Группы
Отклонения
От среднего
Квадраты
Отклонений
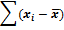
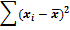
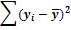
Формулировка гипотез:
Но: Средняя скорость сложной сенсомоторной реакции выбора в экспериментальной группе не выше, чем в контрольной.
Н1: Средняя скорость сложной сенсомоторной реакции выбора в экспериментальной группе выше, чем в контрольной.
Алгоритм подсчёта критерия t :
1*) Мы должны убедиться, что переменные X и Y распределены нормально, или их распределение согласуется с нормальным. (Установление данного факта выходит за рамки данного пособия. При необходимости можно использовать учебник Е.В. Сидоренко).
2) Находим суммы и средние значения в экспериментальной и контрольной группах.
а) В экспериментальной группе среднее арифметическое: 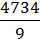 = 526.
= 526.
б) В контрольной группе среднее арифметическое: 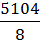 = 638.
= 638.
в) Разница по абсолютной величине между средними:
| 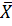 -
- 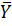 | = |526 – 638| = 112.
| = |526 – 638| = 112.
3) Заполняем 4-ый столбец таблицы. Для этого от каждого значения X (второй столбец) вычитаем среднее значение (526). Результат записываем в соответствующую строку. Если расчёты проведены без ошибок, сумма всех значений 4-го столбца должна равняться нулю.
4) Аналогично заполняем 5-ый столбец, работая со значениями переменной Y (третий столбец) и соответствующим средним значением (638).
5) Заполняем 6-ой столбец таблицы. Для этого каждое значение 4-го столбца возводим в квадрат. Сумма всех значений 6-го столбца записывается в последней строке (28632).
6) Аналогично заполняется 7-ой столбец на основании данных пятого столбца. Сумма значений данного столбца составит 18174.
7) Подсчитывается значение величины Sd по формуле:
Sd= 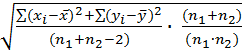 =
= 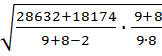 =
= 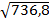 =27,14
=27,14
8) Вычисляем t-критерий Стьюдента по формуле:
tэмп = 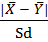 =
= 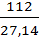 = 4,1
= 4,1
9) Рассчитываем число степеней свободы:
k = 9 + 8 – 2 = 15
10) По Таблице 9 приложения находим критические значения t критерия для k = 15:
tкр = 2,13 (для Р 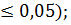 tкр = 2,95 (для Р
tкр = 2,95 (для Р 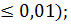 tкр = 4,07 (для Р
tкр = 4,07 (для Р 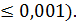
11) Строим ось значимости, наносим критические и эмпирическое значения критерия. В нашем случае tэмп= 4,1 попало в зону значимости правее tкр = 4,07 (для Р 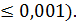
| Зона незначимости |
| Зона значимости 0,001 |
| 2,13 2.95 4,07 tэмп= 4,1 |
| 0,05 0,01 |
12) Делаем вывод. Гипотеза Н0 о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза Н1 о различии между экспериментальной и контрольной группами.
Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более, чем на 0,1% уровне. Иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, не занимающихся спортом активно.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
№1. В классе 25 учащихся. Из них 10 девочек, а остальные – мальчики. Подсчитать процентное содержание девочек и мальчиков в классе.
№2. Во время экзамена в группе из 20 студентов получено 4 пятёрки, 10 четвёрок, а остальные студенты получили тройки. Подсчитать процентное содержание различных оценок в группе.
№3. Во время эксперимента подбрасывалась монетка 30 раз. В результате 14 раз выпал «орел», а в остальных случаях – «решка». Подсчитать процентное содержание выпадений «орла» и «решки» в эксперименте.
№4. Проранжировать показатели в таблице. Сделать проверку.
| № испытуемых п/п | Показатели зрительной памяти | Ранги |
| 1 | 3 | |
| 2 | 9 | |
| 3 | 6 | |
| 4 | 4 | |
| 5 | 5 | |
| 6 | 6 | |
| 7 | 4 | |
| 8 | 4 | |
| 9 | 8 |
№5. Проранжировать показатели в таблице. Сделать проверку.
| № испытуемых п/п | Показатели внимания | Ранги |
| 1 | 38 | |
| 2 | 25 | |
| 3 | 27 | |
| 4 | 25 | |
| 5 | 31 | |
| 6 | 34 | |
| 7 | 39 | |
| 8 | 38 | |
| 9 | 23 | |
| 10 | 25 |
№6. Проранжировать показатели в таблице. Сделать проверку.
| № испытуемых п/п | Показатели тревожности | Ранги |
| 1 | 2 | |
| 2 | 5 | |
| 3 | 7 | |
| 4 | 2 | |
| 5 | 3 | |
| 6 | 5 | |
| 7 | 1 | |
| 8 | 5 | |
| 9 | 0 |
№7. Составить статистический ряд для следующих значений по выборке.:
10, 15, 34, 17, 15, 26, 15, 30, 17, 15, 17, 26, 17, 25, 28, 20, 17, 25, 20, 15.
Найти числовые характеристики распределения.
№8. Составить статистический ряд для следующих значений по выборке:
4, 0, 1, 5, 2, 1, 0, 1, 2, 1, 5, 4, 2, 1, 4, 5, 0, 2, 2, 1.
Найти числовые характеристики распределения.
№9. Составить статистический ряд для следующих значений по выборке:
13, 15, 11, 13, 17, 20, 13, 25, 11, 11, 17, 25, 20, 11, 13, 15, 13, 20, 15, 11.
Найти числовые характеристики распределения.
№10. Составить статистический ряд для следующих значений по выборке:
12, 4, 10, 12, 6, 9, 6, 8, 12, 10, 10, 4, 6, 10, 12, 9, 9, 4, 10, 12.
Найти числовые характеристики распределения.
№11. Составить статистический ряд для следующих значений по выборке:
54, 56, 59, 50, 57, 55, 50, 54, 59, 50, 56, 50, 54, 54, 50, 55, 56, 59, 55, 54.
Найти числовые характеристики распределения.
№12. Составить статистический ряд для следующих значений по выборке:
107, 98, 105, 103, 100, 98, 99, 100, 99, 98, 105, 103, 99, 100, 99, 105, 103, 100, 105, 100.
№13. Составить статистический ряд для следующих значений по выборке:
25, 21, 29, 21, 26, 31, 21, 35, 31, 29, 25, 35, 21, 31, 35, 21, 25, 21, 35, 35.
Найти числовые характеристики распределения.
№14. Получив отрицательный результат, психолог внёс в способ тренинга соответствующие коррективы. Он снова выдвигает гипотезу: улучшенный способ тренинга позволяет эффективно снижать уровень тревожности испытуемых. Для проверки этого утверждения психолог провёл аналогичный эксперимент, но уже на большей выборке испытуемых. В таблице приведены результаты. (Применить критерий знаков G).
| № испытуемых п/п | Уровень тревожности «до» тренинга | Уровень тревожности «после» тренинга | Сдвиг |
| 1 | 24 | 22 | |
| 2 | 12 | 12 | |
| 3 | 40 | 23 | |
| 4 | 30 | 31 | |
| 5 | 40 | 32 | |
| 6 | 35 | 24 | |
| 7 | 40 | 40 | |
| 8 | 32 | 12 | |
| 9 | 40 | 22 | |
| 10 | 24 | 21 | |
| 11 | 33 | 30 | |
| 12 | 38 | 26 | |
| 13 | 39 | 38 | |
| 14 | 25 | 23 | |
| 15 | 28 | 22 | |
| 16 | 36 | 22 | |
| 17 | 37 | 36 | |
| 18 | 32 | 38 | |
| 19 | 25 | 25 |
№15. Психолог выясняет вопрос, будут ли обнаружены различия в успешности решения двух, различных по сложности мыслительных задач. Для решения этого вопроса группа из 120 учащихся решала оба типа задач. Полученные результаты представлены в таблице.
|
|
|
Первая задача |
Сумма | |
| Решена верно | Решена неверно | |||
| Вторая задача | Решена верно | А = 50 | В = 31 | 81 |
| Решена неверно | С = 19 | D = 20 | 39 | |
| Сумма | 69 | 51 | 120 | |
Решить задачу, используя критерий Макнамары.
№16. Используя тест Векслера психолог определил показатели интеллекта у двух групп учащихся из городской и сельской школы. Его интересует вопрос – будут ли обнаружены статистически значимые различия в показателях интеллекта, если в городской выборке 11 детей, а в сельской 12? Полученные показатели:
- в городской выборке: 96, 104, 120, 120, 126, 134, 130, 120, 120, 104, 100;
- в сельской выборке: 120, 110, 102, 96, 84, 82, 76, 82, 88, 100, 104, 118. Применить U-критерий Манна – Уитни.
№17. Самостоятельно провести «исследование». Выбрать 2 различные выборки (по качеству и количеству). Например, 5 юношей и 7 девушек. Или 6 младших школьников и 4 бабушки и т.д.
Всем испытуемым предложить назвать любое число от 1 до 5. Результаты «исследования» записать.
Проверить различие между выборками по признаку «любимое число» с помощью U-критерия.
№18. В двух школах района психолог выяснял мнения учителей об организации психологической службы в школе. Психолога интересовал вопрос: в какой школе психологическая служба поставлена лучше? Учителя давали ответы по номинативной шкале – нравится (да), не нравится – (нет). В первой школе было опрошено 20 учителей (15 ответили «да», 5 – «нет»). Во второй школе – 15 учителей (7 – «да», 8 – «нет»).
№19. Психолог сравнивает два эмпирических распределения, в каждом из которых было обследовано 200 человек по тесту интеллекта. Вопрос: различаются ли между собой эти два распределения? Эмпирические данные представлены в виде таблицы:
| Уровни интеллекта |
Частоты | |
| 1 гр | 2 гр | |
| 60-69 | 1 | 1 |
| 70-79 | 5 | 3 |
| 80-89 | 17 | 7 |
| 90-99 | 45 | 22 |
| 100-109 | 70 | 88 |
| 110-119 | 51 | 69 |
| 120-129 | 10 | 7 |
| 130-139 | 1 | 2 |
| 140-149 | 0 | 1 |
№20. Психолог сравнивает два эмпирических распределения, в каждом из которых было обследовано по тесту интеллекта разное количество испытуемых. Вопрос: различаются ли между собой эти два распределения? Эмпирические данные представлены в виде таблицы:
| Уровни интеллекта |
Частоты | |
| 1 гр | 2 гр | |
| 60-69 | 1 | 0 |
| 70-79 | 8 | 0 |
| 80-89 | 23 | 1 |
| 90-99 | 30 | 11 |
| 100-109 | 38 | 18 |
| 110-119 | 12 | 14 |
| 120-129 | 7 | 3 |
| 130-139 | 4 | 4 |
| 140-149 | 1 | 1 |
| 150-159 | 0 | 1 |
№21. Влияет ли уровень интеллекта на профессиональные достижения? Для решения этой задачи 90 человек оценили по степени их профессиональных достижений и по уровню интеллекта. При разбиении на уровни (градации признака) по обоим признакам было взято три уровня. Все эмпирические данные (частоты) представлены в таблице.
| IQ | Дата: 2019-02-02, просмотров: 893. | ||