1) Определить те значения признака, которые будут критерием для разделения испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта».
2) Подсчитать количества испытуемых, у которых «есть эффект» в первой и во второй группах.
3) Определить процентные доли испытуемых, у которых «есть эффект», путём отнесения их количества к общему числу испытуемых в данной группе (выборке).
4) Проверить, не равняется ли одна из сопоставляемых процентных долей нулю. Если это так, попробовать изменить это, сдвинув точку разделения групп в ту или иную сторону. Если это невозможно, отказаться от данного критерия и использовать критерий c2.
5) Определить по Таблице 6 величины углов j для каждой из сопоставленных процентных долей.
6) Подсчитать эмпирическое значение j по формуле:
j эмп = ( j 1 - j 2 ) ·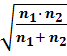 
где j1 – угол, соответствующий большей процентной доле;
j2 – угол, соответствующий меньшей процентной доле;
n1 – количество наблюдений в выборке 1;
n2 – количество наблюдений в выборке 2.
7) Сопоставить полученное значение jэмп с критическими значениями, которые постоянны:
jкр = 1,64 (Р≤ 0,05); jкр = 2,31 (Р≤ 0,01),
построив ось значимости.
8) Сформулировать выводы.
Пример 7.3. Психолог провёл эксперимент, в котором выяснилось, что из 23 учащихся математической спецшколы 15 справились с заданием, а из 28 обычной школы с тем же заданием справились 11 человек. Можно ли считать, что различия в успешности решения заданий учащимися спецшколы и обычной школы достоверны?
Решение: с помощью критерия Фишера φ.
Формулировка гипотез:
Н0: Различий в успешности решения заданий учащимися спецшколы и обычной школы нет.
Н1: Различия в успешности решения заданий учащимися спецшколы и обычной школы существуют.
Алгоритм подсчёта критерия j :
1) Критерием для разделения групп является успешность в выполнении задания.
2) Показатели успешности выполнения заданий необходимо перевести в проценты:
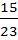·100% = 65,2% для спецшколы;
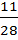·100% = 39,3% для обычной школы.
3) По Таблице 6 находим величины φ1 и φ2, соответствующие процентным долям в каждой группе.
Для 65,2% φ1=1,880, а для 39,3% φ2 = 1,355.
4) Подсчитываем эмпирическое значение φэмп по формуле:
j эмп = ( j 1 - j 2 ) ·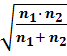
где n1 – количество наблюдений в выборке 1;
n2 - количество наблюдений в выборке 2.
В нашем случае φэмп = (1,880 – 1,355) 
= 1,86
5) Критические значения имеют фиксированную величину и составляют:
jкр = 1,64 (Р≤ 0,05); jкр = 2,31 (Р≤ 0,01).
6) Строим ось значимости. φэмп попало в зону неопределённости.
| 0,05 Зона неопределённости 0,01 |
| 1,64 1,86 2,31 |
7) Вывод. На 5% уровне значимости можно говорить о различии между успешностью в решении заданий учениками сравниваемых школ, а на уровне в 1% этого утверждать нельзя. На основании сравнения процентных долей можно утверждать, что учащиеся спецшколы успешнее справились с заданием, чем учащиеся обычной школы.
Вопросы для обсуждения
1. Какие статистические методы называются критериями согласия распределений? Каковы задачи, решаемые с помощью данных методов?
2. Назовите основные критерии согласия распределений? В чём состоят их различия?
3. Каково назначение критерия хи-квадрат? В чём состоит смысл данного метода? Какова формулировка гипотез?
4. Каковы условия применения критерия хи-квадрат?
5. Какие основные типы задач решаются с помощью применения критерия хи-квадрат? Какова формулировка гипотез?
6. Каково назначение критерия Фишера - φ? В чём состоит смысл данного метода? Какова формулировка гипотез? Почему данный критерий называется угловым преобразованием Фишера?
7. Каковы условия применения критерия Фишера - φ?
8. Какие основные типы задач решаются с помощью применения критерия Фишера - φ?
9. Каков алгоритм подсчёта критерия Фишера - φ?
Дата: 2019-02-02, просмотров: 665.
