1) Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.
2) Распределения переменных X и Y должны быть близки к нормальному.
3) Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.
4) Таблицы уровней значимости для коэффициента корреляции (Таблица 7) рассчитаны от n = 7 до n = 1000. Оценка уровня значимости осуществляется при числе степеней свободы k = n – 2.
Сравнение коэффициентов корреляции можно провести, решив одну и ту же задачу различными способами. В Примере 8.1. задача решена с помощью коэффициента ранговой корреляции Спирмена. Пример 8.3. – это решение той же самой задачи с помощью коэффициента линейной корреляции Пирсона.
Пример 8.3. 20 школьникам были розданы тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Решение: Введём переменные: X – среднее время решения наглядно-образных, Y – среднее время решения вербальных тестов. Данные переменные измерены в шкале отношений. (Переменные распределены нормально. Этот факт нуждается в дополнительной проверке, которая здесь опускается). Ответ на вопрос получим с помощью критерия линейной корреляции Пирсона. Исходные данные представлены в виде таблицы.
| № испытуемых п/п | X Среднее время решения наглядно-образных заданий | Y Среднее время решения вербальных заданий | X 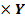
| X 2 | Y 2 |
| 1 | 19 | 17 | 323 | 361 | 289 |
| 2 | 32 | 7 | 224 | 1024 | 49 |
| 3 | 33 | 17 | 561 | 1089 | 289 |
| 4 | 44 | 28 | 1232 | 1936 | 784 |
| 5 | 28 | 27 | 756 | 784 | 729 |
| 6 | 35 | 31 | 1085 | 1225 | 961 |
| 7 | 39 | 20 | 780 | 1521 | 400 |
| 8 | 39 | 17 | 663 | 1521 | 289 |
| 9 | 44 | 35 | 1540 | 1936 | 1225 |
| 10 | 44 | 43 | 1892 | 1936 | 1849 |
| 11 | 24 | 10 | 240 | 576 | 100 |
| 12 | 37 | 28 | 1036 | 1369 | 784 |
| 13 | 29 | 13 | 377 | 841 | 169 |
| 14 | 40 | 43 | 1720 | 1600 | 1849 |
| 15 | 42 | 45 | 1890 | 1764 | 2025 |
| 16 | 32 | 24 | 768 | 1024 | 576 |
| 17 | 48 | 45 | 2160 | 2304 | 2025 |
| 18 | 42 | 26 | 1092 | 1764 | 676 |
| 19 | 33 | 16 | 528 | 1089 | 256 |
| 20 | 47 | 26 | 1222 | 2209 | 676 |
| Сумма | 731 | 518 | 20.089 | 27.873 | 16.000 |
Формулировка гипотез:
Н0: Корреляция между средним временем решения наглядно-образных и вербальных заданий не отличается от нуля.
Н1: Корреляция между средним временем решения наглядно-образных и вербальных заданий достоверно отличается от нуля.
Алгоритм подсчёта коэффициента корреляции Пирсона:
1) Заполняем все столбцы таблицы, рассчитать суммы.
2) Рассчитываем эмпирическую величину коэффициента корреляции по формуле:
rxy = 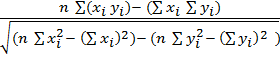 =
=
= 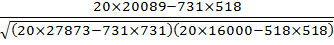 = 0,669
= 0,669
3) Находим критические значения коэффициента корреляции по Таблице 7. Число степеней свободы: k = n – 2 = 20 – 2 = 18.
r кр = 0,44 (Р≤0,05); r кр = 0,56 (Р≤0,01).
4) Строим ось значимости. rxy попадает в зону значимости.
| 0,05 0,01 |
| Зона значимости |
| 0,44 0,56 0,669 |
5) Вывод. Отвергается Н0 и принимается Н1. Связь между временем решения наглядно-образных и вербальных задач статистически значима на 1% уровне и положительна. Полученная прямо пропорциональная зависимость говорит о том, что чем выше среднее время решения наглядно-образных задач, тем выше среднее время решения вербальных задач и наоборот.
Таким образом, подтвердился результат решения данной задачи методом ранговой корреляции Спирмена.
Вопросы для обсуждения
1. Что такое «корреляционня связь»? В чём отличие функциональной и корреляционной зависимости?
2. Какая корреляционная связь называется линейной, положительной, отрицательной, нулевой?
3. Каковы основные коэффициенты корреляции и основание для их классификации? Какова область значений коэффициента корреляции?
4. Какова общая классификация корреляционных связей?
5. Какова частная классификация корреляционных связей?
6. Какова корреляционная связь, если коэффициент корреляции:
а) r = 0,55;
б) r = 0,05;
в) r = 0,55 (Р ≤ 0,05);
г) r = 0,75 (Р ≤ 0,01);
д) r = 0,75 (Р ≤ 0,001).
7. Каково назначение рангового коэффициента корреляции Спирмена? Каков смысл данного метода? Какова формулировка гипотез?
8. Каковы условия применения рангового коэффициента корреляции Спирмена?
9. Каков алгоритм подсчёта рангового коэффициента корреляции Спирмена?
10. Каковы основные типы задач, решаемые методом ранговой корреляции?
11. Каково назначение коэффициента линейной корреляции Пирсона? Каков смысл данного метода? Какова формулировка гипотез?
12. Каковы условия применения коэффициента линейной корреляции Пирсона?
13. Каков алгоритм подсчёта коэффициента линейной корреляции Пирсона? 14. Проведите сопоставительный анализ коэффициентов корреляции Спирмена и Пирсона.
15. Вы хотите выявить корреляционную связь между уровнем самоактуализации и уровнем профессионального выгорания педагогов школы. В вашей выборке 35 педагогов. Какой статистический метод вы примените?
16. Что необходимо изменить в условиях вашего исследования, чтобы можно было применить другой метод выявления корреляционной связи?
17. Вы выявили, что существует корреляционная связь между уровнем развития абстрактного мышления и возрастом учеников. Можно ли назвать данную связь зависимостью? Что, в таком случае, будет являться независимой переменной, а что зависимой?
Дата: 2019-02-02, просмотров: 857.