1) Составить список испытуемых в любом порядке, например, алфавитном.
2) Вычислить разность между индивидуальными значениями во втором и первом замерах («после» - «до»). Определить, что будет считаться «типичным» сдвигом и сформулировать соответствующие гипотезы.
3) Перевести разности в абсолютные величины и записать их отдельным столбцом.
4) Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчётной.
5) Отметить какими-либо значками ранги, соответствующие сдвигам в «нетипичном» направлении. Подсчитать сумму этих рангов по формуле:
Тэмп = 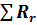 ,
,
где Rr - ранговые значения с более редким знаком.
6) Определить критические значения Т для данного n по Таблице 2.
7) Построить ось значимости, определить зону попадания Тэмп.
8) Сделать выводы.
Пример 5.2. Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить, будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений?
Решение: Для решения задачи психолог у 19 детей определяет количество ошибок при выполнении корректурной пробы до и после коррекционных упражнений. В таблице приведены соответствующие экспериментальные данные и дополнительные столбцы, необходимые для работы по парному критерию Т – Вилкоксона.
| № испытуемых п/п | До | После | Сдвиг (значение разности с учётом знака) | Абсолютные величины разностей | Ранги абсолютных величин разностей | Символ нетипичного сдвига |
| 1 | 24 | 22 | -2 | 2 | 10,5 | |
| 2 | 12 | 12 | 0 | 0 | 2 | |
| 3 | 42 | 41 | -1 | 1 | 6,5 | |
| 4 | 30 | 31 | +1 | 1 | 6,5 | * |
| 5 | 40 | 32 | -8 | 8 | 15 | |
| 6 | 55 | 44 | -11 | 11 | 16 | |
| 7 | 50 | 50 | 0 | 0 | 2 | |
| 8 | 52 | 32 | -20 | 20 | 18 | |
| 9 | 50 | 32 | -18 | 18 | 17 | |
| 10 | 22 | 21 | -1 | 1 | 6,5 | |
| 11 | 33 | 34 | +1 | 1 | 6,5 | * |
| 12 | 78 | 56 | -22 | 22 | 19 | |
| 13 | 79 | 78 | -1 | 1 | 6,5 | |
| 14 | 25 | 23 | -2 | 2 | 10,5 | |
| 15 | 28 | 22 | -6 | 6 | 13,5 | |
| 16 | 16 | 12 | -4 | 4 | 12 | |
| 17 | 17 | 16 | -1 | 1 | 6,5 | |
| 18 | 12 | 18 | +6 | 6 | 13,5 | * |
| 19 | 25 | 25 | 0 | 0 | 2 | |
| Сумма | - | - | - | - | 190 | Тэмп=26,5 |
Формулировка гипотез:
H0: Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении.
H1: Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении.
Гипотезы могут быть также сформулированы следующим образом:
Н0: сдвиг в сторону уменьшения количества ошибок после коррекционной работы является случайным.
Н1: сдвиг в сторону уменьшения количества ошибок после коррекционной работы не является случайным.
Подсчёт критерия Т – Вилкоксона:
1) Заполняется таблица экспериментальных данных (1, 2, 3 столбцы).
2) В четвёртый столбец таблицы вносят величины сдвигов с учётом знака. Их вычисляют путём вычитания из чисел третьего столбца соответствующих чисел второго столбца.
3) В пятом столбце каждому значению сдвига ставят его соответствующую абсолютную величину.
4) В шестом столбце ранжируют абсолютные величины сдвигов, представленных в пятом столбце. Подсчитывают сумму рангов (в нашем примере она = 190). Подсчитывают сумму рангов по формуле: N(N+1)\2 = 19·20/2 = 190. Убеждаемся в правильности ранжирования (190=190, ранжирование проведено правильно).
5) Символом (*) отмечают все имеющиеся в таблице нетипичные сдвиги. В нашем случае – это три положительных сдвига. Суммируют ранги нетипичных сдвигов. Это и будет искомая величина Тэмп.
Тэмп= 6,5+13,5+6,5 = 26,5
6) По Таблице 2 определяют критические значения Ткр для n=19. Нужная строка таблицы:
| n | P | |
| 0,05 | 0,01 | |
| 19 | 53 | 37 |
7) Строим ось значимости. Полученная величина Тэмп = 26,5 попадает в зону значимости.
| 0,05 0,01 |
| Зона значимости |
| 53 38 26,5 |
8) Можно утверждать, следовательно, что зафиксированные в эксперименте изменения неслучайны и значимы на 1% уровне. Таким образом, применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы.
Поскольку преобладание типичного отрицательного направления сдвига в данном конкретном эксперименте не является случайным, то должна быть принята гипотеза Н1 о наличии различий, а гипотеза Н0 отклонена.
Вопросы для обсуждения
1. Каково назначение критериев различий? Какова их специфика и основания для классификации?
2. Что такое «мощность критерия различий»? Как мощность критерия связана с его сложностью?
3. Чем отличаются параметрические и непараметрические критерии различий? Какие критерии более универсальны?
4. Каковы рекомендации к выбору критерия различий?
5. Назовите основные непараметрические критерии для связных выборок. Каковы области их применения и назначение?
6. Каково назначение критерия знаков G? В чём состоит смысл данного критерия? Какова формулировка статистических гипотез?
7. Каковы условия применения критерия знаков G?
8. Каков алгоритм подсчёта критерия знаков G?
9. Каково назначение парного критерия Т - Вилкоксона? В чём состоит смысл данного критерия? Какова формулировка статистических гипотез?
10. Каковы условия применения парного критерия Т - Вилкоксона?
11. Каков алгоритм подсчёта парного критерия Т - Вилкоксона?
12. Что называется «сдвигом» при измерении какого-либо признака? Какой сдвиг называется типичным, какой нетипичным?
13. Проведите сопоставительный анализ критерия знаков G и парного критерия Т – Вилкоксона.
Дата: 2019-02-02, просмотров: 848.