Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых мер. Это мода, медиана, среднее арифметическое, разброс выборки, дисперсия, стандартное отклонение.

Мода – такое числовое значение, которое встречается в выборке наиболее часто. Обозначается иногда как 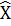 (или Мо).

Пример 3.1. Определить моду в ряду значений: (2, 6, 6, 8, 9, 9, 9, 10).

Решение: модой является число 9, т.к. 9 встречается чаще других значений. 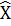=9.

Правила нахождения моды

1) Если все значения в выборке встречаются одинаковое число раз, говорят, что выборочный ряд не имеет моды.

2) Когда 2 соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих значений.

Пример 3.2. Имеется ряд значений: (1, 2, 2, 2, 5, 5, 5, 6). Частоты смежных значений 2 и 5 совпадают и равны 3. Эта частота больше, чем частота других значений 1 и 6. Следовательно, модой этого ряда будет величина 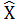 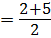= 3,5.

3) Если два несмежных (не соседних) значения в выборке имеют равные значения, которые больше частот любого другого значения, то выделяют две моды. В этом случае выборку называют бимодальной. Могут существовать и мультимодальные ряды.

Медиана – это значение, которое делит упорядоченное множество данных пополам. Обозначается как 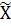 (или Md).

Пример 3.3. Найти медиану выборки: 9, 3, 5, 8, 4, 11, 13.

Решение: Сначала упорядочим выборку по величинам входящих в неё значений: (3, 4, 5, 8, 9, 11, 13). В выборке 7 элементов, следовательно, четвёртый по порядку элемент (8) будет средним (до него – 3 элемента и после него 3 элемента). Таким образом, медианой будет четвёртый элемент: 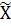=8.

Пример 3.4. Найти медиану выборки: 20, 9, 13, 1, 4, 11.

Решение: Упорядочим выборку: (1, 4, 9, 11, 13, 20). Поскольку имеется чётное число элементов, то существует две «середины» - 9 и 11. В этом случае медиана определяется как среднее арифметическое этих значений:

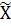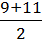 =  = 10.

Среднее арифметическое ряда из n числовых значений Х₁, Х₂, … Х_n обозначается 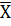(икс с чертой) и вычисляется как:

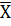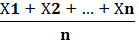 = =  ( ΣХ _i )

В том случае, если отдельные значения выборки повторяются, среднюю арифметическую вычисляют по формуле:

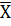 =   (Σ x_i f_i ),         где f_i – частоты повторяющихся значений.

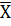 в таком случае называют взвешенной средней.

Средние величины характеризуют выборку одним (средним) числом. Их преимущество состоит в способности уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, отличает данную выборку от другой. Однако, среднее как статистический показатель не лишено недостатков. Поэтому в статистике, кроме средней величины, используются и другие характеристики «типичных значений» - мода и медиана.