МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
Учебно-методическое пособие
Ульяновск
2017
УДК 15.073 Печатается по решению редакционно-издательского
ББК 88 совета ФГБОУ ВО «Ульяновский государственный
С 87 педагогический университет имени И. Н. Ульянова»
Рецензенты:
Коноплёва И. В. – кандидат физико-математических наук,
доцент кафедры математики ФГБОУ ВПО УлГУ;
Гурылева Л. В. – кандидат психологических наук, доцент кафедры психологии
ФГБОУ ВО «УлГПУ им. И. Н. Ульянова»
ISBN
С 87 Стрюкова Г. А. Методы математической статистики в психолого-педагогических исследованиях: Учебно-методическое пособие. Ульяновск: УлГПУ, 2017. 91 с.
В учебном пособии рассматриваются основные методы статистической обработки эмпирических и экспериментальных данных, включая непараметрические и параметрические критерии оценки различий, согласия распределений, корреляционный анализ. Приведены необходимые теоретические сведения и формулы для решения типовых задач, наиболее часто встречающихся в экспериментальных психологических исследованиях. На конкретных примерах рассмотрены алгоритмы решения типовых задач. В качестве приложения к учебному пособию приведены справочные таблицы для определения критических значений основных статистических критериев, задания для самостоятельного решения.
Учебное пособие предназначено для студентов психологических специальностей. Пособие также может быть использовано студентами других специальностей педагогического вуза в качестве справочника при написании выпускных квалификационных и курсовых работ.
УДК 15.073
ББК 88
© Стрюкова Г. А.
© ФГБОУ ВО
«УлГПУ им. И. Н. Ульянова»
Содержание
| Введение......................................................................................................... | 4 |
| Классификатор методов математической статистики................ | 6 |
| 1. Понятие измерения в психологии. Измерительные шкалы................... | 7 |
| 2. Выборка. Формы учёта результатов измерений..................................... | 13 |
| 3. Числовые характеристики распределений. Нормальное распределение............................................................................................ | 17 |
| 4. Общие принципы проверки статистических гипотез............................. | 22 |
| 5. Статистические критерии различий. Непараметрические критерии для связных выборок.…………................................................................ | 27 |
| G-критерий знаков......................................................................................... | 28 |
| Т-критерий Вилкоксона ............................................................................... | 31 |
| 6. Непараметрические критерии для несвязных выборок………………. | 35 |
| U-критерий Манна-Уитни............................................................................. | 36 |
| Q-критерий Розенбаума................................................................................. | 40 |
| 7. Критерии согласия распределений..……………...…............................. | 42 |
Критерий 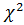 .................................................................................................. ..................................................................................................
| 43 |
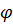 -критерий Фишера ...................................................................................... -критерий Фишера ......................................................................................
| 47 |
| 8. Корреляционный анализ. Коэффициенты корреляции Спирмена и Пирсона………………………………………………………................... | 51 |
| 9. Параметрические критерии различий...................................................... | 62 |
| Задания для самостоятельного решения................................................. | 67 |
| Темы рефератов........................................................................................... | 78 |
| Таблицы критических значений................................................................ | 79 |
| Рекомендуемая литература....................................................................... | 91 |
ВВЕДЕНИЕ
Перед человеком, вставшим на путь психологического или педагогического исследования, рано или поздно возникает проблема обоснования его результатов. Любое исследование подразумевает применение валидных методик, назначение которых – выявлять проявление (количественное или качественное) какого-либо признака у испытуемых, то есть что-либо измерять или устанавливать наличие (отсутствие). Таким образом, молодой учёный оказывается обладателем целого ряда (нескольких рядов) численных значений и имеет возможность стать также и математиком.
Простейшие математические процедуры, известные из курса элементарной (школьной) математики, как то: подсчёт общего числа испытуемых в какой-либо группе, вычисление процентного содержания, то есть так называемая описательная статистика, безусловно, необходимы, но далеко не достаточны для научного исследования. Даже если были получены очень хорошие результаты, например: до эксперимента в группе у 35% испытуемых проявлялся какой-либо признак (высокий уровень тревожности и т.д.), а после эксперимента – всего лишь у 5%. Предъявление результатов эксперимента на данном уровне (уровне описательной статистики) не может служить доказательством эффективности экспериментального воздействия.
Наряду с описательной статистикой должны быть использованы статистические методы более высокого уровня – подсчёт различных критериев или коэффициентов. Каждый из них предназначен для «своей» области. Для одного и того же случая могут оказаться применимыми не один, а целый ряд методов. Какие это методы и как их использовать, каковы области их применения – на эти вопросы даны ответы в данном пособии.
Пособие содержит описание лишь некоторых статистических методов, на наш взгляд, наиболее адекватных научному исследованию на начальных этапах – на уровне курсовой работы по психологии или выпускной квалификационной работы по психологии и педагогике. В ходе описания каждого метода математической статистики сохраняется логика изложения: приводится описание и назначение метода, условия и алгоритм его применения. В завершении рассматривается пример с подробным решением, доказательством психологической гипотезы данным методом математической статистики. В пособие включён раздел «Задания для самостоятельного решения», предназначенный для использования на практических и семинарских занятиях по предмету «Математические основы психологии».
Материал пособия отобран из основных признанных и современных учебников и учебных пособий по дисциплине. В наибольшей степени это относится к учебнику «Математическая статистика для психологов» О. Ю. Ермолаева и работе «Методы математической обработки в психологии» Е. В. Сидоренко. Это очень разные книги: и написаны различным языком, и ориентированы на очень разные сферы. На наш взгляд, если вы хотите расширить свои знания по математическим методам (рассмотреть не один, а несколько примеров, познакомиться с другими методами на уровне нашего пособия) – используйте учебник О. Ю. Ермолаева. Если же ваша задача – пойти «вглубь»: узнать о смысле метода, представить его графическую интерпретацию, познакомиться с другими обозначениями величин – вам необходим учебник Е. В. Сидоренко. Последний содержит, кроме этого, и интересные, нестандартные психологические задачи, взятые «из жизни».
Обе указанные работы содержат справочные таблицы так называемых критических значений, без которых невозможно обойтись при работе с математическими методами в психологических и педагогических исследованиях. Часть данного справочного материала, необходимого для работы с отобранными нами в качестве основных методами, приводится и в нашем пособии в разделе «Таблицы критических значений».
Знакомство с методами математической статистики предваряют три первых темы данного пособия, в которых определяется понятийный аппарат дисциплины, отрабатываются основные навыки, необходимые для использования методов.
Для желающих освоить более быстрый способ получения результата в начале пособия представлен Классификатор методов математической статистики. С его помощью можно подобрать необходимый для вашей научной работы метод и осваивать целенаправленно работу с ним, используя только необходимые темы данного пособия. Ссылки на страницы с подробным описанием каждого метода приведены в Содержании.
Пособие в целом может быть рекомендовано в качестве методического сопровождения соответствующих дисциплин бакалавриата и магистратуры психолого-педагогического направления. В конце пособия представлены темы для рефератов по данным дисциплинам и список рекомендуемой литературы.
Понятие измерения.
Измерение – это процедура, с помощью которой измеряемый объект сравнивается с некоторым эталоном, в результате чего получается численное выражение в определённом масштабе или шкале.
Единица измерения – условный эталон для осуществления тех или иных измерительных процедур.
В естественных науках и технике существуют стандартные единицы измерения (градус, метр, ампер и т.д.). Психологические переменные (за единичными исключениями) не имеют собственных измерительных единиц. В психологии измерение осуществляется с помощью кодирования.
Кодирование – это такая операция, с помощью которой экспериментальным данным придаётся форма числового сообщения (кода).
Научно-исследовательскую работу психолога, проводящего эксперимент, можно представить по следующей схеме:
ИССЛЕДОВАТЕЛЬ (психолог)
¯
предмет исследования (психические свойства, процессы, функции, …)
¯
испытуемый (группа испытуемых)
¯
эксперимент (измерение)
¯
данные эксперимента (числовые коды)
¯
статистическая обработка данных эксперимента
¯
результат статистической обработки (числовые коды)
¯
выводы (печатный текст: отчёт, диплом, статья и т.д.)
¯
ПОЛУЧАТЕЛЬ НАУЧНОЙ ИНФОРМАЦИИ (руководитель курсовой, дипломной или кандидатской работы, заказчик, читатель статьи и т.д.)
Измерительные шкалы.
Значение психологического признака определяется с помощью специальных измерительных шкал. Согласно С. Стивенсу (1951), существует 4 типа измерительных шкал (способов измерения):
1) номинативная, номинальная или шкала наименований;
2) порядковая, ординарная или ранговая шкала;
3) интервальная или шкала равных интервалов;
4) шкала равных отношений, или шкала отношений.
Все находящиеся в одной строке наименования являются синонимами и используются на равных основаниях. Применение процедуры измерения возможно только 4-мя перечисленными способами. Причём каждая шкала имеет собственную, отличную от других, форму кода, систему фиксации статистического материала, соответствующие статистические методы обработки.
Измерения, осуществляемые с помощью первых двух шкал, считаются качественными, а осуществляемые с помощью двух последних шкал, количественными.
Самое главное, о чём должен помнить психолог при выборе способа измерения, это то, что он должен соответствовать поставленной задаче.
Правила ранжирования.
Особенности ранжирования числовых характеристик:
1) Наименьшему числовому значению приписывается ранг 1.
2) Наибольшему числовому значению приписывается ранг, равный количеству ранжируемых величин.
3) В случае если несколько исходных значений оказываются равными, то им приписывается ранг, равный средней величине тех рангов, которые эти величины получили бы, если они стояли по порядку друг за другом и не были бы равны.
4) Общая сумма реальных рангов должна совпадать с расчётной, определяемой по формуле:
Сумма рангов = 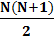
5) Не рекомендуется ранжировать более чем 20 величин (признаков, качеств, свойств и т.п.), поскольку в этом случае ранжирование оказывается малоустойчивым.
6) При необходимости ранжирования достаточно большого количества объектов их следует объединить по какому-либо признаку в достаточно однородные классы (группы), а затем уже ранжировать полученные классы (группы).
Пример 1.1. У 11-ти испытуемых получены показатели невербального интеллекта, которые представлены в таблице. Проранжируйте эти показатели. Сделайте проверку правильности ранжирования.
Решение: Необходимо заполнить третий столбец таблицы. Числа в скобках – вспомогательные записи в случае равных значений. В нашем случае – это значение 117. Оно встречается дважды (восьмым и девятым по порядку). Следовательно, ранг этого значения равен среднему арифметическому чисел 8 и 9, т.е. 8,5.
| № испытуемых п/п | Показатели интеллекта | Ранги |
| 1 | 113 | 6 |
| 2 | 107 | 4 |
| 3 | 123 | 11 |
| 4 | 122 | 10 |
| 5 | 117 | (8) 8,5 |
| 6 | 117 | (9) 8,5 |
| 7 | 105 | 3 |
| 8 | 108 | 5 |
| 9 | 114 | 7 |
| 10 | 102 | 1 |
| 11 | 104 | 2 |
Проверка:
1) Сумма рангов: 6+4+11+10+8,5+8,5+3+5+7+1+2=66
2) По формуле: 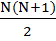 =
= 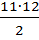 =11
=11  6 = 66
6 = 66
3) Сравниваем результаты: 66 = 66, следовательно, ранжирование проведено верно.
Вопросы для обсуждения
1. Что называется измерением, единицей измерения? Чем отличается измерение в психологии от измерения в естественных науках и технике?
2. Что такое кодирование? На каких этапах научного исследования психолог работает с числовыми кодами?
3. Какие типы измерительных шкал существуют? Каковы принципиальные различия между типами шкал?
4. Каковы особенности, примеры и частные случаи номинативной шкалы? Каковы другие названия данной шкалы? Какие статистические методы применимы к данной шкале?
5. Ранговая шкала: её особенности, примеры. Другие названия ранговой шкалы. Статистические методы, применимые в ранговой шкале.
6. Что такое ранжирование? Каковы правила ранжирования?
7. Как осуществить проверку правильности ранжирования?
8. Каковы рекомендации по ранжированию большого количества величин?
9. Шкала интервалов: особенности, примеры. Интервал и его размер. Применимость статистических методов к шкале интервалов.
10. Шкала отношений и её отличие от шкалы интервалов. Применимость шкалы отношений в психологии.
11. Вы измеряете согласие девятиклассников на продолжение обучения в профильном классе школы. Школьник может дать ответ «Да» или «Нет». В какой шкале осуществляется данное измерение?
12. Проводится измерение веса и роста младших школьников. В какой шкале осуществляется измерение?
13. Вы определяете быстроту реакции военных лётчиков. Для этого фиксируется время ответа испытуемого на световой сигнал. В какой шкале проводится данное измерение?
14. Какие измерения вы можете провести в своей группе, чтобы они были проведены:
а) в шкале наименований;
б) в ординарной шкале;
в) в интервальной шкале;
г) в шкале равных отношений?
15. Какие психологические методики позволяют осуществлять измерение в шкале интервалов?
Виды соотношений выборок
1) Независимые (несвязные) выборки. Если процедура эксперимента и полученные результаты одной выборки не оказывают влияния на особенности протекания процедуры и результаты другой выборки.
2) Зависимые (связные) выборки. Если процедура эксперимента и полученные результаты одной выборки оказывают влияние на другую выборку. Одна и та же выборка, на которой дважды проводилось психологическое обследование (пусть даже разных психологических качеств, особенностей), является зависимой (связной).
Уровень готовности
К школьному обучению
Уровень адаптации к школе
Всего
Таблица позволяет выявить тенденцию, заключающуюся в том, что первоклассники, подготовленные к школьному обучению, как правило, лучше адаптируются к школе.
Таким образом, правильно составленные таблицы – большое подспорье в экспериментальной работе. Кроме таблиц (простых и сложных) группировка экспериментальных данных может осуществляться в виде статистических рядов.
2) Статистические ряды. Чаще всего используются вариационные ранжированные статистические ряды. Это двойной ряд чисел, в котором первая строка – значения признака (варианты, xi), расположенные в порядке возрастания, а вторая строка – частоты вариант (сколько раз каждая варианта встречается в выборке, fi). Сумма частот должна быть равна объёму выборки: Σ fi = n.
Статистический ряд может содержать третью строку – относительные частоты вариант ni, которые определяются как отношение частоты к объёму выборки: ni =  . Сумма относительных частот должна равняться 1. Относительные частоты могут быть представлены в процентах: ni =
. Сумма относительных частот должна равняться 1. Относительные частоты могут быть представлены в процентах: ni =  100%.
100%.
Пример 2.3. Психолог провёл тестирование интеллекта по тесту Векслера у 25 школьников, и сырые баллы по второму субтесту оказались следующими: 6; 9; 5; 7; 10; 8; 9; 10; 8; 11; 9; 12; 9; 8; 10; 11; 9; 10; 8; 10; 7; 9; 10; 9; 11. Записать данные в виде статистического ряда.
Решение: n = 25. Статистический ряд имеет вид:
| Варианта xi | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Σ |
| Частота варианты fi | 1 | 1 | 2 | 4 | 7 | 6 | 3 | 1 | 25 |
| Относительная частота варианты ni (или %) | 0,04 (4%) | 0,04 (4%) | 0,08 (8%) | 0,16 (16%) | 0,28 (28%) | 0,24 (24%) | 0,12 (12%) | 0,04 (4%) | 1 (100 %) |
Вопросы для обсуждения
1. Дайте определение генеральной совокупности и приведите примеры генеральных совокупностей. Каков объём генеральной совокупности?
2. В чём заключается полное психологическое исследование? В каких случаях оно возможно? В чём преимущество и недостатки такого исследования?
3. Выборка и её объём. Репрезентативность выборки. Респондент. Выборочное исследование.
4. В чём различие между понятиями «независимые выборки» и «несвязные выборки»? Между «независимые выборки» и «зависимые выборки»?
5. В вашей группе проведены два исследования: на выявление мотивов учения и определение типа темперамента. Со сколькими выборками пришлось в данном случае работать исследователю?
6. Что называется группировкой экспериментального материала? Каковы возможные виды группировки?
7. Каковы отличия простых статистических таблиц от сложных? Как проверить правильность составления данных таблиц?
8. Что называется статистическим рядом?
9. Что называется вариантой, её частотой и относительной частотой?
10. Как представить относительную частоту в процентах? Как проверить правильность составления статистического ряда?
11. Многопольные таблицы. Приведите пример четырёхпольной, восьмипольной таблиц. Может ли таблица быть семипольной?
Число степеней свободы.
Число степеней свободы ( n ) – это число свободно варьирующих единиц в составе выборки. Оно равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся объём выборки (n), средние и дисперсии.
Число степеней свободы у выборочного ряда определяется:
n = n – 1, где n – общее число элементов ряда (выборки).
При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы определяется по формуле:
ν = n – k, где k – число ограничений свободы вариации.
Для таблицы экспериментальных данных число степеней свободы определяется следующим образом:
ν = ( c – 1) ( n – 1), где c – число столбцов, а n – число строк таблицы (число испытуемых).
Для ряда статистических методов подсчёт числа степеней свободы оказывается необходимым и рассчитывается по-своему.
Вопросы для обсуждения
1. Мода и правила её нахождения. Какая выборка называется мономодальной, бимодальной, полимодальной?
2. Что можно назвать модой признака «оценка за экзамен в последнюю сессию» в вашей группе?
3. Медиана и правила её нахождения.
3. Среднее арифметическое, взвешенная средняя. Преимущества и недостатки средних значений при характеристике выборки.
4. Разброс выборки. Связь между размахом выборки и силой варьирования признака.
5. Дисперсия и стандартное отклонение. Их смысл и правила вычисления.
6. Число степеней свободы и правила его вычисления.
7. Распределение признака. Ряд распределения.
8. Нормальное распределение, его особенности. Распространённость нормального распределения в психологии.
Результат проверки гипотезы
Н0
Вопросы для обсуждения
1. Что называется статистической гипотезой, математической статистикой?
2. Что называется нулевой гипотезой и альтернативной гипотезой? Каковы их обозначения и смысл?
3. В каких случаях гипотеза отклоняется или не отклоняется? Каковы возможные ошибки в этих случаях?
4. Что называется уровнем значимости? Как обозначается уровень значимости, каковы возможные его значения? Каков смысл этих значений?
5. Какой из уровней значимости выше: 0,05 или 0,01?
6. Что такое «ось значимости»? Как определяется её направление? Какие зоны выделяют на оси значимости?
7. Как определить критические значения для какого-либо статистического метода? Сколько их существует?
8. О чём свидетельствует попадание эмпирического значения в зону значимости?
9. О чём свидетельствует попадание эмпирического значения в зону незначимости?
10. О чём свидетельствует попадание эмпирического значения в зону неопределённости?
11. Каковы этапы принятия статистического решения?
12. Как находится эмпирическое значение какой-либо статистической величины?
13. Вы измеряете уровень тревожности в двух первых классах. Какие гипотезы вы можете сформулировать?
14. Вы проверяете уровень тревожности и уровень креативности у сотрудников фирмы. Какие гипотезы вы можете сформулировать?
15. Вы определяете отношение уровня интеллекта школьника к среднему уровню интеллекта всего класса. Какие гипотезы вы формулируете?
16. Какие эмпирические исследования соответствуют следующим гипотезам:
Н0: Уровень подготовленности к школе у выпускников детского сада не выше, чем у детей, не посещавших детские дошкольные учреждения?
Н1: Уровень подготовленности к школе у выпускников детского сада выше, чем у детей, не посещавших детские дошкольные учреждения?
17. Назовите ошибки, допущенные при формулировке следующих гипотез:
Н0: Уровень интеллекта у мальчиков младшего школьного возраста выше, чем у девочек того же возраста.
Н1: Уровень интеллекта у мальчиков младшего школьного возраста ниже, чем у девочек того же возраста.
Сформулируйте гипотезы правильно.
Рекомендации к выбору критерия различий
* Определить связность (несвязность) выборки.
* Определить однородность (неоднородность) выборки.
* Оценить объём выборки, выбрать критерий по данному признаку.
* Начать работу с наименее трудоёмкого критерия.
* Если использованный критерий не выявил различий, применить более мощный, но одновременно более трудоёмкий критерий.
* Если в распоряжении психолога имеется несколько критериев, то следует выбирать тот, который наиболее полно использует информацию, содержащуюся в экспериментальных данных.
* При малом объёме выборки следует увеличивать величину уровня значимости (не менее 1%), т.к. небольшая выборка и низкий уровень значимости приводят к увеличению вероятности принятия ошибочных решений.
Критерий знаков G .
Вопросы для обсуждения
1. Каково назначение критериев различий? Какова их специфика и основания для классификации?
2. Что такое «мощность критерия различий»? Как мощность критерия связана с его сложностью?
3. Чем отличаются параметрические и непараметрические критерии различий? Какие критерии более универсальны?
4. Каковы рекомендации к выбору критерия различий?
5. Назовите основные непараметрические критерии для связных выборок. Каковы области их применения и назначение?
6. Каково назначение критерия знаков G? В чём состоит смысл данного критерия? Какова формулировка статистических гипотез?
7. Каковы условия применения критерия знаков G?
8. Каков алгоритм подсчёта критерия знаков G?
9. Каково назначение парного критерия Т - Вилкоксона? В чём состоит смысл данного критерия? Какова формулировка статистических гипотез?
10. Каковы условия применения парного критерия Т - Вилкоксона?
11. Каков алгоритм подсчёта парного критерия Т - Вилкоксона?
12. Что называется «сдвигом» при измерении какого-либо признака? Какой сдвиг называется типичным, какой нетипичным?
13. Проведите сопоставительный анализ критерия знаков G и парного критерия Т – Вилкоксона.
U -критерий Манна – Уитни.
Вопросы для обсуждения
1. Назовите основные непараметрические критерии для несвязных выборок. Каковы области их применения?
2. Каково назначение U-критерия Манна – Уитни? Каков смысл данного критерия? Какова формулировка статистических гипотез?
3. Каковы условия применения U-критерия Манна – Уитни?
4. Каков алгоритм подсчёта U-критерия Манна – Уитни?
5. Каково назначение критерия Q Розенбаума? Каков смысл данного критерия? Какова формулировка статистических гипотез?
6. Каковы условия применения критерия Q Розенбаума?
7. Каков алгоритм подсчёта критерия Q Розенбаума?
8. Провести сопоставительный анализ критерия Q Розенбаума и U-критерия Манна – Уитни.
Критерий хи-квадрат.
Решение задач
Оценки
Суммы
Формулировка гипотез:
Н0: Существенной разницы в уровне знаний учащимися алгебры в двух школах не существует.
Н1: Существенная разница в уровне знаний учащимися алгебры в двух школах существует.
Алгоритм подсчёта критерия c 2 :
1) Заполняется восьмипольная таблица.
2) Подсчёт эмпирического значения проводится по формуле:
c 2 эмп = 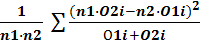
c2эмп = 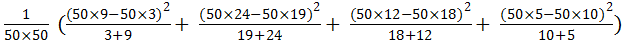 = 6,45
= 6,45
3) Число степеней свободы: n= (4 – 1)·(2 – 1) = 3
4) По Таблице 5 находятся критические значения:
c2кр 1 = 7,815 (Р≤ 0,05); c2кр 2 = 11,345 (Р≤ 0,01).
5) Строится ось значимости. c2эмп попадает в зону незначимости.
| Зона незначимости |
| 6,45 7,815 11,345 |
| 0,05 0,01 |
6) Вывод: принимается гипотеза Н0 о сходстве. Уровни знаний учащимися алгебры в двух разных школах статистически значимо не отличаются.
7.3. Критерий Фишера – φ.
Вопросы для обсуждения
1. Какие статистические методы называются критериями согласия распределений? Каковы задачи, решаемые с помощью данных методов?
2. Назовите основные критерии согласия распределений? В чём состоят их различия?
3. Каково назначение критерия хи-квадрат? В чём состоит смысл данного метода? Какова формулировка гипотез?
4. Каковы условия применения критерия хи-квадрат?
5. Какие основные типы задач решаются с помощью применения критерия хи-квадрат? Какова формулировка гипотез?
6. Каково назначение критерия Фишера - φ? В чём состоит смысл данного метода? Какова формулировка гипотез? Почему данный критерий называется угловым преобразованием Фишера?
7. Каковы условия применения критерия Фишера - φ?
8. Какие основные типы задач решаются с помощью применения критерия Фишера - φ?
9. Каков алгоритм подсчёта критерия Фишера - φ?
Коэффициенты корреляции.
Переменные X и Y могут быть измерены в разных шкалах. Именно это определяет выбор соответствующего коэффициента корреляции.
Тип шкалы
Мера связи
Величина любого коэффициента корреляции лежит в отрезке от -1 до +1. Если получается иначе, следовательно, в расчётах произошла ошибка.
Если коэффициент корреляции по модулю близок к 1, это свидетельствует о высоком уровне связи между переменными. Если близок к 0, связь отсутствует. Если коэффициент положителен, то между переменными существует положительная корреляционная связь. Если коэффициент отрицателен, корреляционная связь отрицательна.
Используются две системы классификации корреляционных связей по их силе: общая и частная.
Вопросы для обсуждения
1. Что такое «корреляционня связь»? В чём отличие функциональной и корреляционной зависимости?
2. Какая корреляционная связь называется линейной, положительной, отрицательной, нулевой?
3. Каковы основные коэффициенты корреляции и основание для их классификации? Какова область значений коэффициента корреляции?
4. Какова общая классификация корреляционных связей?
5. Какова частная классификация корреляционных связей?
6. Какова корреляционная связь, если коэффициент корреляции:
а) r = 0,55;
б) r = 0,05;
в) r = 0,55 (Р ≤ 0,05);
г) r = 0,75 (Р ≤ 0,01);
д) r = 0,75 (Р ≤ 0,001).
7. Каково назначение рангового коэффициента корреляции Спирмена? Каков смысл данного метода? Какова формулировка гипотез?
8. Каковы условия применения рангового коэффициента корреляции Спирмена?
9. Каков алгоритм подсчёта рангового коэффициента корреляции Спирмена?
10. Каковы основные типы задач, решаемые методом ранговой корреляции?
11. Каково назначение коэффициента линейной корреляции Пирсона? Каков смысл данного метода? Какова формулировка гипотез?
12. Каковы условия применения коэффициента линейной корреляции Пирсона?
13. Каков алгоритм подсчёта коэффициента линейной корреляции Пирсона? 14. Проведите сопоставительный анализ коэффициентов корреляции Спирмена и Пирсона.
15. Вы хотите выявить корреляционную связь между уровнем самоактуализации и уровнем профессионального выгорания педагогов школы. В вашей выборке 35 педагогов. Какой статистический метод вы примените?
16. Что необходимо изменить в условиях вашего исследования, чтобы можно было применить другой метод выявления корреляционной связи?
17. Вы выявили, что существует корреляционная связь между уровнем развития абстрактного мышления и возрастом учеников. Можно ли назвать данную связь зависимостью? Что, в таком случае, будет являться независимой переменной, а что зависимой?
T -критерий Стьюдента.
Группы
Отклонения
От среднего
Квадраты
Отклонений
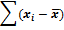
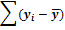
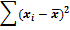
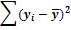
Формулировка гипотез:
Но: Средняя скорость сложной сенсомоторной реакции выбора в экспериментальной группе не выше, чем в контрольной.
Н1: Средняя скорость сложной сенсомоторной реакции выбора в экспериментальной группе выше, чем в контрольной.
Алгоритм подсчёта критерия t :
1*) Мы должны убедиться, что переменные X и Y распределены нормально, или их распределение согласуется с нормальным. (Установление данного факта выходит за рамки данного пособия. При необходимости можно использовать учебник Е.В. Сидоренко).
2) Находим суммы и средние значения в экспериментальной и контрольной группах.
а) В экспериментальной группе среднее арифметическое: 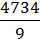 = 526.
= 526.
б) В контрольной группе среднее арифметическое: 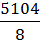 = 638.
= 638.
в) Разница по абсолютной величине между средними:
| 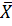 -
- 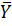 | = |526 – 638| = 112.
| = |526 – 638| = 112.
3) Заполняем 4-ый столбец таблицы. Для этого от каждого значения X (второй столбец) вычитаем среднее значение (526). Результат записываем в соответствующую строку. Если расчёты проведены без ошибок, сумма всех значений 4-го столбца должна равняться нулю.
4) Аналогично заполняем 5-ый столбец, работая со значениями переменной Y (третий столбец) и соответствующим средним значением (638).
5) Заполняем 6-ой столбец таблицы. Для этого каждое значение 4-го столбца возводим в квадрат. Сумма всех значений 6-го столбца записывается в последней строке (28632).
6) Аналогично заполняется 7-ой столбец на основании данных пятого столбца. Сумма значений данного столбца составит 18174.
7) Подсчитывается значение величины Sd по формуле:
Sd= 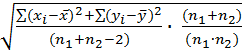 =
= 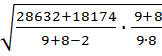 =
= 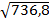 =27,14
=27,14
8) Вычисляем t-критерий Стьюдента по формуле:
tэмп = 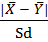 =
= 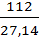 = 4,1
= 4,1
9) Рассчитываем число степеней свободы:
k = 9 + 8 – 2 = 15
10) По Таблице 9 приложения находим критические значения t критерия для k = 15:
tкр = 2,13 (для Р 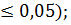 tкр = 2,95 (для Р
tкр = 2,95 (для Р 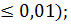 tкр = 4,07 (для Р
tкр = 4,07 (для Р 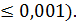
11) Строим ось значимости, наносим критические и эмпирическое значения критерия. В нашем случае tэмп= 4,1 попало в зону значимости правее tкр = 4,07 (для Р 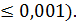
| Зона незначимости |
| Зона значимости 0,001 |
| 2,13 2.95 4,07 tэмп= 4,1 |
| 0,05 0,01 |
12) Делаем вывод. Гипотеза Н0 о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза Н1 о различии между экспериментальной и контрольной группами.
Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более, чем на 0,1% уровне. Иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, не занимающихся спортом активно.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
№1. В классе 25 учащихся. Из них 10 девочек, а остальные – мальчики. Подсчитать процентное содержание девочек и мальчиков в классе.
№2. Во время экзамена в группе из 20 студентов получено 4 пятёрки, 10 четвёрок, а остальные студенты получили тройки. Подсчитать процентное содержание различных оценок в группе.
№3. Во время эксперимента подбрасывалась монетка 30 раз. В результате 14 раз выпал «орел», а в остальных случаях – «решка». Подсчитать процентное содержание выпадений «орла» и «решки» в эксперименте.
№4. Проранжировать показатели в таблице. Сделать проверку.
| № испытуемых п/п | Показатели зрительной памяти | Ранги |
| 1 | 3 | |
| 2 | 9 | |
| 3 | 6 | |
| 4 | 4 | |
| 5 | 5 | |
| 6 | 6 | |
| 7 | 4 | |
| 8 | 4 | |
| 9 | 8 |
№5. Проранжировать показатели в таблице. Сделать проверку.
| № испытуемых п/п | Показатели внимания | Ранги |
| 1 | 38 | |
| 2 | 25 | |
| 3 | 27 | |
| 4 | 25 | |
| 5 | 31 | |
| 6 | 34 | |
| 7 | 39 | |
| 8 | 38 | |
| 9 | 23 | |
| 10 | 25 |
№6. Проранжировать показатели в таблице. Сделать проверку.
| № испытуемых п/п | Показатели тревожности | Ранги |
| 1 | 2 | |
| 2 | 5 | |
| 3 | 7 | |
| 4 | 2 | |
| 5 | 3 | |
| 6 | 5 | |
| 7 | 1 | |
| 8 | 5 | |
| 9 | 0 |
№7. Составить статистический ряд для следующих значений по выборке.:
10, 15, 34, 17, 15, 26, 15, 30, 17, 15, 17, 26, 17, 25, 28, 20, 17, 25, 20, 15.
Найти числовые характеристики распределения.
№8. Составить статистический ряд для следующих значений по выборке:
4, 0, 1, 5, 2, 1, 0, 1, 2, 1, 5, 4, 2, 1, 4, 5, 0, 2, 2, 1.
Найти числовые характеристики распределения.
№9. Составить статистический ряд для следующих значений по выборке:
13, 15, 11, 13, 17, 20, 13, 25, 11, 11, 17, 25, 20, 11, 13, 15, 13, 20, 15, 11.
Найти числовые характеристики распределения.
№10. Составить статистический ряд для следующих значений по выборке:
12, 4, 10, 12, 6, 9, 6, 8, 12, 10, 10, 4, 6, 10, 12, 9, 9, 4, 10, 12.
Найти числовые характеристики распределения.
№11. Составить статистический ряд для следующих значений по выборке:
54, 56, 59, 50, 57, 55, 50, 54, 59, 50, 56, 50, 54, 54, 50, 55, 56, 59, 55, 54.
Найти числовые характеристики распределения.
№12. Составить статистический ряд для следующих значений по выборке:
107, 98, 105, 103, 100, 98, 99, 100, 99, 98, 105, 103, 99, 100, 99, 105, 103, 100, 105, 100.
№13. Составить статистический ряд для следующих значений по выборке:
25, 21, 29, 21, 26, 31, 21, 35, 31, 29, 25, 35, 21, 31, 35, 21, 25, 21, 35, 35.
Найти числовые характеристики распределения.
№14. Получив отрицательный результат, психолог внёс в способ тренинга соответствующие коррективы. Он снова выдвигает гипотезу: улучшенный способ тренинга позволяет эффективно снижать уровень тревожности испытуемых. Для проверки этого утверждения психолог провёл аналогичный эксперимент, но уже на большей выборке испытуемых. В таблице приведены результаты. (Применить критерий знаков G).
| № испытуемых п/п | Уровень тревожности «до» тренинга | Уровень тревожности «после» тренинга | Сдвиг |
| 1 | 24 | 22 | |
| 2 | 12 | 12 | |
| 3 | 40 | 23 | |
| 4 | 30 | 31 | |
| 5 | 40 | 32 | |
| 6 | 35 | 24 | |
| 7 | 40 | 40 | |
| 8 | 32 | 12 | |
| 9 | 40 | 22 | |
| 10 | 24 | 21 | |
| 11 | 33 | 30 | |
| 12 | 38 | 26 | |
| 13 | 39 | 38 | |
| 14 | 25 | 23 | |
| 15 | 28 | 22 | |
| 16 | 36 | 22 | |
| 17 | 37 | 36 | |
| 18 | 32 | 38 | |
| 19 | 25 | 25 |
№15. Психолог выясняет вопрос, будут ли обнаружены различия в успешности решения двух, различных по сложности мыслительных задач. Для решения этого вопроса группа из 120 учащихся решала оба типа задач. Полученные результаты представлены в таблице.
|
|
|
Первая задача |
Сумма | |
| Решена верно | Решена неверно | |||
| Вторая задача | Решена верно | А = 50 | В = 31 | 81 |
| Решена неверно | С = 19 | D = 20 | 39 | |
| Сумма | 69 | 51 | 120 | |
Решить задачу, используя критерий Макнамары.
№16. Используя тест Векслера психолог определил показатели интеллекта у двух групп учащихся из городской и сельской школы. Его интересует вопрос – будут ли обнаружены статистически значимые различия в показателях интеллекта, если в городской выборке 11 детей, а в сельской 12? Полученные показатели:
- в городской выборке: 96, 104, 120, 120, 126, 134, 130, 120, 120, 104, 100;
- в сельской выборке: 120, 110, 102, 96, 84, 82, 76, 82, 88, 100, 104, 118. Применить U-критерий Манна – Уитни.
№17. Самостоятельно провести «исследование». Выбрать 2 различные выборки (по качеству и количеству). Например, 5 юношей и 7 девушек. Или 6 младших школьников и 4 бабушки и т.д.
Всем испытуемым предложить назвать любое число от 1 до 5. Результаты «исследования» записать.
Проверить различие между выборками по признаку «любимое число» с помощью U-критерия.
№18. В двух школах района психолог выяснял мнения учителей об организации психологической службы в школе. Психолога интересовал вопрос: в какой школе психологическая служба поставлена лучше? Учителя давали ответы по номинативной шкале – нравится (да), не нравится – (нет). В первой школе было опрошено 20 учителей (15 ответили «да», 5 – «нет»). Во второй школе – 15 учителей (7 – «да», 8 – «нет»).
№19. Психолог сравнивает два эмпирических распределения, в каждом из которых было обследовано 200 человек по тесту интеллекта. Вопрос: различаются ли между собой эти два распределения? Эмпирические данные представлены в виде таблицы:
| Уровни интеллекта |
Частоты | |
| 1 гр | 2 гр | |
| 60-69 | 1 | 1 |
| 70-79 | 5 | 3 |
| 80-89 | 17 | 7 |
| 90-99 | 45 | 22 |
| 100-109 | 70 | 88 |
| 110-119 | 51 | 69 |
| 120-129 | 10 | 7 |
| 130-139 | 1 | 2 |
| 140-149 | 0 | 1 |
№20. Психолог сравнивает два эмпирических распределения, в каждом из которых было обследовано по тесту интеллекта разное количество испытуемых. Вопрос: различаются ли между собой эти два распределения? Эмпирические данные представлены в виде таблицы:
| Уровни интеллекта |
Частоты | |
| 1 гр | 2 гр | |
| 60-69 | 1 | 0 |
| 70-79 | 8 | 0 |
| 80-89 | 23 | 1 |
| 90-99 | 30 | 11 |
| 100-109 | 38 | 18 |
| 110-119 | 12 | 14 |
| 120-129 | 7 | 3 |
| 130-139 | 4 | 4 |
| 140-149 | 1 | 1 |
| 150-159 | 0 | 1 |
№21. Влияет ли уровень интеллекта на профессиональные достижения? Для решения этой задачи 90 человек оценили по степени их профессиональных достижений и по уровню интеллекта. При разбиении на уровни (градации признака) по обоим признакам было взято три уровня. Все эмпирические данные (частоты) представлены в таблице.
| IQ |
Код Имени Участ- Ника |
Измерение |
Измерение | ||||||||||||
|
Активное слушание |
Снижение эмо- Ционального Напряжения |
Аргумента- Ция |
Активное слушание |
Снижение эмо- Ционального Напряжения |
Аргумента- Ция | ||||||||||
| Реал | Идеал | Реал | Идеал | Реал | Идеал | Реал | Идеал | Реал | Идеал | Реал | Идеал | ||||
| 1 | И. | 6 | 9 | 5 | 8 | 5 | 8 | 7 | 10 | 6 | 10 | 7 | 9 | ||
| 2 | Я. | 3 | 5 | 1 | 3 | 4 | 5 | 5 | 7 | 4 | 6 | 5 | 7 | ||
| 3 | Ин. | 4 | 6 | 4 | 6 | 5 | 8 | 8 | 10 | 7 | 8 | 6 | 8 | ||
| 4 | Р. | 4 | 6 | 4 | 5 | 5 | 7 | 6 | 7 | 5 | 7 | 5 | 7 | ||
| 5 | К. | 6 | 9 | 4 | 9 | 4 | 8 | 4 | 10 | 5 | 10 | 5 | 10 | ||
| 6 | Н. | 6 | 8 | 5 | 8 | 3 | 6 | 8 | 9 | 7 | 9 | 6 | 8 | ||
| 7 | Е. | 3 | 8 | 5 | 10 | 2 | 6 | 7 | 8 | 8 | 10 | 5 | 7 | ||
| 8 | Ле. | 6 | 9 | 5 | 8 | 3 | 7 | 5 | 8 | 7 | 10 | 5 | 9 | ||
| 9 | Ли. | 6 | 8 | 5 | 9 | 5 | 9 | 7 | 8 | 6 | 9 | 5 | 9 | ||
| 10 | Т. | 5 | 8 | 6 | 9 | 5 | 8 | 7 | 10 | 7 | 10 | 6 | 10 | ||
| 11 | Ет. | 6 | 8 | 6 | 10 | 3 | 9 | 5 | 10 | 4 | 9 | 3 | 9 | ||
| 12 | Б. | 6 | 8 | 3 | 10 | 4 | 7 | 7 | 9 | 6 | 8 | 5 | 8 | ||
Вопросы:
1. Ощущаются ли участниками достоверные сдвиги в уровне владения каждым из трёх навыков после тренинга?
2. Произошли ли по трём группам навыков разные сдвиги, или эти сдвиги для разных навыков примерно одинаковы?
3. Уменьшается ли расхождение между «идеальным» и реальным уровнями владения навыками после тренинга?
4. Произошли ли под влиянием тренинга достоверные изменения в представлении участников об «идеальном» владении навыками?
№ 25. Наблюдателем установлено, что 51 человек из 70-ти выбрал правую дорожку при переходе из точки А в точку Б, а 19 человек – левую. Можно ли утверждать, что правая дорожка предпочиталась достоверно чаще?
№ 26. В тренинге профессиональных наблюдателей допускается, чтобы наблюдатель ошибался в оценке возраста ребёнка не более, чем на 1год в ту или иную сторону. Наблюдатель допускается к работе, если он совершает не более 15% ошибок, превышающих отклонение на 1 год. Наблюдатель Н допустил одну ошибку в 50 попытках, а наблюдатель К – 15 ошибок в 50 попытках. Достоверно ли отличаются эти результаты от контрольной величины?
№ 27. В эксперименте испытуемый должен произвести выбор левого или правого стола с заданиями. В инструкции психолог подчёркивает, что задания на обоих столах одинаковы. Из 150 испытуемых правый стол выбрали 98 человек, а левый 52. Можно ли утверждать, что подобный выбор левого или правого стола равновероятен или он обусловлен какой-либо причиной, неизвестной психологу?
№ 28. Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года. Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлению в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем. (Результаты представлены в таблице).
| № учащихся п/п | Ранги показателей школьной готовности | Ранги среднегодовой успеваемости |
| 1 | 3 | 2 |
| 2 | 5 | 7 |
| 3 | 6 | 8 |
| 4 | 1 | 3 |
| 5 | 4 | 4 |
| 6 | 11 | 6 |
| 7 | 9 | 11 |
| 8 | 2 | 1 |
| 9 | 8 | 10 |
| 10 | 7 | 5 |
| 11 | 10 | 9 |
№ 29. Провести самостоятельное исследование на сравнение двух несвязных выборок по проявлению одного и того же признака. Определить исследуемый признак, необходимый объём выборок, адекватный метод математической статистики; осуществить эмпирическое исследование, математическую обработку результатов; сформулировать выводы.
Если возможно применение нескольких математических методов при решении данной задачи, указать все, а задачу решить одним (любым из указанных). Пояснить, почему данный метод оказался предпочтительным.
№ 30. Провести самостоятельное исследование на выявление связи между двумя признаками в одной и той же выборке.
№ 31. Психолог поставил цель выявить, существует ли связь между самоактуализацией педагогов и уровнем профессионального «выгорания». Исследована выборка педагогов одной школы в составе 16 учителей. Самоактуализация изучалась по тесту САМОАЛ по 10 субшкалам; профессиональное «выгорание» - по методике, адаптированной для педагогических специальностей. Согласно ей феномен профессионального «выгорания» может быть представлен следующими показателями: эмоциональное истощение, деперсонализация, редукция личных достижений. В таблице приведены данные по выборке по следующим показателям: субшкалы теста САМОАЛ (взгляд на природу человека; креативность; автономность; аутосимпатия) и показатели профессионального «выгорания». Определить, между какими шкалами существует связь. Как можно это интерпретировать?
| № Педагога П/п |
Самоактуализация (субшкалы САМОАЛ) |
ТЕМЫ РЕФЕРАТОВ 1. Непараметрические критерии для связных выборок. Критерий Фридмана. 2. Непараметрические критерии для связных выборок. Критерий тенденций Пейджа. 3. Непараметрические критерии для связных выборок. Критерий Макнамары. 4. Непараметрические критерии для несвязных выборок. Критерий тенденций Джонкира. 5. Геометрическая интерпретация углового преобразования Фишера. 6. Критерий Колмогорова – Смирнова. 7. Параметрические критерии различий. t-критерий Стьюдента. 8. Параметрические критерии различий. F-критерий Фишера. 9. Многофункциональные критерии. Биномиальный критерий m. 10. Расчёт уровней значимости коэффициентов корреляции. 11. Расчёт рангового коэффициента корреляции Спирмена в случае равных рангов. 12. Коэффициент корреляции «φ». 13. Бисериальный и рангово-бисериальный коэффициенты корреляции. 14. Коэффициент корреляции τ Кендалла. 15. Корреляционное отношение Пирсона η. 16. Однофакторный дисперсионный анализ для несвязных выборок. 17. Однофакторный дисперсионный анализ для связных выборок. 18. Критерии дисперсионного анализа. Критерий Линка и Уоллеса. 19. Критерии дисперсионного анализа. Критерий Немени. 20. Двухфакторный дисперсионный анализ для несвязных выборок. 21. Двухфакторный дисперсионный анализ для связных выборок. 22. Основные понятия и смысл регрессионного анализа. 23. Понятие о факторном анализе и его применении в психологии. 24. История создания и применения в психологических исследованиях математических методов. Таблица 1. 0,01 | ||||||||||
| 5 | 0 | - | 27 | 8 | 7 | 49 | 18 | 15 | 92 | 37 | 34 | |
| 6 | 0 | 0 | 28 | 8 | 7 | 50 | 18 | 16 | 94 | 38 | 35 | |
| 7 | 0 | 0 | 29 | 9 | 7 | 52 | 19 | 17 | 96 | 39 | 36 | |
| 8 | 1 | 0 | 30 | 10 | 8 | 54 | 20 | 18 | 98 | 40 | 37 | |
| 9 | 1 | 0 | 31 | 10 | 8 | 56 | 21 | 18 | 100 | 41 | 37 | |
| 10 | 1 | 0 | 32 | 10 | 8 | 58 | 22 | 19 | 110 | 45 | 42 | |
| 11 | 2 | 1 | 33 | 11 | 9 | 60 | 23 | 20 | 120 | 50 | 46 | |
| 12 | 2 | 1 | 34 | 11 | 9 | 62 | 24 | 21 | 130 | 55 | 51 | |
| 13 | 3 | 1 | 35 | 12 | 10 | 64 | 24 | 22 | 140 | 59 | 55 | |
| 14 | 3 | 2 | 36 | 12 | 10 | 66 | 25 | 23 | 150 | 64 | 60 | |
| 15 | 3 | 2 | 37 | 13 | 10 | 68 | 26 | 23 | 160 | 69 | 64 | |
| 16 | 4 | 2 | 38 | 13 | 11 | 70 | 27 | 24 | 170 | 73 | 69 | |
| 17 | 4 | 3 | 39 | 13 | 11 | 72 | 28 | 25 | 180 | 78 | 73 | |
| 18 | 5 | 3 | 40 | 14 | 12 | 74 | 29 | 26 | 190 | 83 | 78 | |
| 19 | 5 | 4 | 41 | 14 | 12 | 76 | 30 | 27 | 200 | 87 | 83 | |
| 20 | 5 | 4 | 42 | 15 | 13 | 78 | 31 | 28 | 220 | 97 | 92 | |
| 21 | 6 | 4 | 43 | 15 | 13 | 80 | 32 | 29 | 240 | 106 | 101 | |
| 22 | 6 | 5 | 44 | 16 | 13 | 82 | 33 | 30 | 260 | 116 | 110 | |
| 23 | 7 | 5 | 45 | 16 | 14 | 84 | 33 | 30 | 280 | 125 | 120 | |
| 24 | 7 | 5 | 46 | 16 | 14 | 86 | 34 | 31 | 300 | 135 | 129 | |
| 25 | 7 | 6 | 47 | 17 | 15 | 88 | 35 | 32 |
| |||
| 26 | 8 | 6 | 48 | 17 | 15 | 90 | 36 | 33 |
| |||
Таблица 2.
Таблица 3.
Продолжение таблицы 3.
p = 0 ,05
| n1 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 21 | 19 | 26 | 34 | 41 | 49 | 57 | 65 | 73 | 81 | 89 | 97 | 105 | 113 | 121 | 130 | 138 | 146 | 154 |
| 22 | 20 | 28 | 36 | 44 | 52 | 60 | 69 | 77 | 85 | 94 | 102 | 111 | 119 | 128 | 136 | 145 | 154 | 162 |
| 23 | 21 | 29 | 37 | 46 | 55 | 63 | 72 | 81 | 90 | 99 | 107 | 116 | 125 | 134 | 143 | 152 | 161 | 170 |
| 24 | 22 | 31 | 39 | 48 | 57 | 66 | 75 | 85 | 94 | 103 | 113 | 122 | 131 | 141 | 150 | 160 | 169 | 179 |
| 25 | 23 | 32 | 41 | 50 | 60 | 69 | 79 | 89 | 98 | 108 | 118 | 128 | 137 | 147 | 157 | 167 | 177 | 187 |
| 26 | 24 | 33 | 43 | 53 | 62 | 72 | 82 | 93 | 103 | 113 | 123 | 133 | 143 | 154 | 164 | 174 | 185 | 195 |
| 27 | 25 | 35 | 45 | 55 | 65 | 75 | 86 | 96 | 107 | 118 | 128 | 139 | 150 | 160 | 171 | 182 | 193 | 203 |
| 28 | 26 | 36 | 47 | 57 | 68 | 79 | 89 | 100 | 111 | 122 | 133 | 144 | 156 | 167 | 178 | 189 | 200 | 212 |
| 29 | 27 | 38 | 48 | 59 | 70 | 82 | 93 | 104 | 116 | 127 | 139 | 150 | 162 | 173 | 185 | 196 | 208 | 220 |
| 30 | 28 | 39 | 50 | 62 | 73 | 85 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 |
| 31 | 29 | 41 | 52 | 64 | 76 | 88 | 100 | 112 | 124 | 137 | 149 | 161 | 174 | 186 | 199 | 211 | 224 | 236 |
| 32 | 30 | 42 | 54 | 66 | 78 | 91 | 103 | 116 | 129 | 141 | 154 | 167 | 180 | 193 | 206 | 219 | 232 | 245 |
| 33 | 31 | 43 | 56 | 68 | 81 | 94 | 107 | 120 | 133 | 146 | 159 | 173 | 186 | 199 | 213 | 226 | 239 | 253 |
| 34 | 32 | 45 | 58 | 71 | 84 | 97 | 110 | 124 | 137 | 151 | 164 | 178 | 192 | 206 | 219 | 233 | 247 | 261 |
| 35 | 33 | 46 | 59 | 73 | 86 | 100 | 114 | 128 | 142 | 156 | 170 | 184 | 198 | 212 | 226 | 241 | 255 | 269 |
| 36 | 35 | 48 | 61 | 75 | 89 | 103 | 117 | 132 | 146 | 160 | 175 | 189 | 204 | 219 | 233 | 248 | 263 | 278 |
| 37 | 36 | 49 | 63 | 77 | 92 | 106 | 121 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 271 | 286 |
| 38 | 37 | 51 | 65 | 79 | 94 | 109 | 124 | 139 | 155 | 170 | 185 | 201 | 216 | 232 | 247 | 263 | 278 | 294 |
| 39 | 38 | 52 | 67 | 82 | 97 | 112 | 128 | 143 | 159 | 175 | 190 | 206 | 222 | 238 | 254 | 270 | 286 | 302 |
| 40 | 39 | 53 | 69 | 84 | 100 | 115 | 131 | 147 | 163 | 179 | 196 | 212 | 228 | 245 | 261 | 278 | 294 | 311 |
p = 0,01
| n1 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 21 | 10 | 16 | 22 | 29 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 113 | 120 | 127 |
| 22 | 10 | 17 | 23 | 30 | 37 | 45 | 52 | 59 | 66 | 74 | 81 | 89 | 96 | 104 | 111 | 119 | 127 | 134 |
| 23 | 11 | 18 | 25 | 32 | 39 | 47 | 55 | 62 | 70 | 78 | 86 | 94 | 102 | 109 | 117 | 125 | 133 | 141 |
| 24 | 12 | 19 | 26 | 34 | 42 | 49 | 57 | 66 | 74 | 82 | 90 | 98 | 107 | 115 | 123 | 132 | 140 | 149 |
| 25 | 12 | 20 | 27 | 35 | 44 | 52 | 60 | 69 | 77 | 86 | 95 | 103 | 112 | 121 | 130 | 138 | 147 | 156 |
| 26 | 13 | 21 | 29 | 37 | 46 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 136 | 145 | 154 | 163 |
| 27 | 14 | 22 | 30 | 39 | 48 | 57 | 66 | 75 | 85 | 94 | 103 | 113 | 122 | 132 | 142 | 151 | 161 | 171 |
| 28 | 14 | 23 | 32 | 41 | 50 | 59 | 69 | 78 | 88 | 98 | 108 | 118 | 128 | 138 | 148 | 158 | 168 | 178 |
| 29 | 15 | 24 | 33 | 42 | 52 | 62 | 72 | 82 | 92 | 102 | 112 | 123 | 133 | 143 | 154 | 164 | 175 | 185 |
| 30 | 15 | 25 | 34 | 44 | 54 | 64 | 75 | 85 | 95 | 106 | 117 | 127 | 138 | 149 | 160 | 171 | 182 | 192 |
| 31 | 16 | 26 | 36 | 46 | 56 | 67 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 155 | 166 | 177 | 188 | 200 |
| 32 | 17 | 27 | 37 | 47 | 58 | 69 | 80 | 91 | 103 | 114 | 126 | 137 | 149 | 160 | 172 | 184 | 195 | 207 |
| 33 | 17 | 28 | 38 | 49 | 60 | 72 | 83 | 95 | 106 | 118 | 130 | 142 | 154 | 166 | 178 | 190 | 202 | 214 |
| 34 | 18 | 29 | 40 | 51 | 62 | 74 | 86 | 98 | 110 | 122 | 134 | 147 | 159 | 172 | 184 | 197 | 209 | 222 |
| 35 | 19 | 30 | 41 | 53 | 64 | 77 | 89 | 101 | 114 | 126 | 139 | 152 | 164 | 177 | 190 | 203 | 216 | 229 |
| 36 | 19 | 31 | 42 | 54 | 67 | 79 | 92 | 104 | 117 | 130 | 143 | 156 | 170 | 183 | 196 | 210 | 223 | 236 |
| 37 | 20 | 32 | 44 | 56 | 69 | 81 | 95 | 108 | 121 | 134 | 148 | 161 | 175 | 189 | 202 | 216 | 230 | 244 |
| 38 | 21 | 33 | 45 | 58 | 71 | 84 | 97 | 111 | 125 | 138 | 152 | 166 | 180 | 194 | 208 | 223 | 237 | 251 |
| 39 | 21 | 34 | 46 | 59 | 73 | 86 | 100 | 114 | 128 | 142 | 157 | 171 | 185 | 200 | 214 | 229 | 244 | 258 |
| 40 | 22 | 35 | 48 | 61 | 75 | 89 | 103 | 117 | 132 | 146 | 161 | 176 | 191 | 206 | 221 | 236 | 251 | 266 |
Таблица 4.
Таблица 5.
Критические значения критерия χ2 Пирсона
| ν | p | ν | p | ν | p | |||
| 0,05 | 0,01 | 0,05 | 0,01 | 0,05 | 0,01 | |||
| 1 | 3,841 | 6,635 | 35 | 49,802 | 57,342 | 69 | 89,391 | 99,227 |
| 2 | 5,991 | 9,210 | 36 | 50,998 | 58,619 | 70 | 90,631 | 100,425 |
| 3 | 7,815 | 11,345 | 37 | 52,192 | 59,892 | 71 | 91,670 | 101,621 |
| 4 | 9,488 | 13,277 | 38 | 53,384 | 61,162 | 72 | 92,808 | 102,816 |
| 5 | 11,070 | 15,086 | 39 | 54,572 | 62,428 | 73 | 93,945 | 104,010 |
| 6 | 12,592 | 16,812 | 40 | 55,758 | 63,691 | 74 | 95,081 | 105,202 |
| 7 | 14,067 | 18,475 | 41 | 56,942 | 64,950 | 75 | 96,217 | 106,393 |
| 8 | 15,507 | 20,090 | 42 | 58,124 | 66,206 | 76 | 97,351 | 107,582 |
| 9 | 16,919 | 21,666 | 43 | 59,304 | 67,459 | 77 | 98,484 | 108,771 |
| 10 | 18,307 | 23,209 | 44 | 60,481 | 68,709 | 78 | 99,617 | 109,958 |
| 11 | 19,675 | 24,725 | 45 | 61,656 | 69,957 | 79 | 100,749 | 111,144 |
| 12 | 21,026 | 26,217 | 46 | 62,830 | 71,201 | 80 | 101,879 | 112,329 |
| 13 | 22,362 | 27,688 | 47 | 64,001 | 72,443 | 81 | 103,010 | 113,512 |
| 14 | 23,685 | 29,141 | 48 | 65,171 | 73,683 | 82 | 104,139 | 114,695 |
| 15 | 24,996 | 30,578 | 49 | 66,339 | 74,919 | 83 | 105,267 | 115,876 |
| 16 | 26,296 | 32,000 | 50 | 67,505 | 76,154 | 84 | 106,395 | 117,057 |
| 17 | 27,587 | 33,409 | 51 | 68,669 | 77,386 | 85 | 107,522 | 118,236 |
| 18 | 28,869 | 34,805 | 52 | 69,832 | 78,616 | 86 | 108,648 | 119,414 |
| 19 | 30,144 | 36,191 | 53 | 70,993 | 79,843 | 87 | 109,773 | 120,591 |
| 20 | 31,410 | 37,566 | 54 | 72,153 | 81,069 | 88 | 110,898 | 121,767 |
| 21 | 32,671 | 38,932 | 55 | 73,311 | 82,292 | 89 | 112,022 | 122,942 |
| 22 | 33,924 | 40,289 | 56 | 74,468 | 83,513 | 90 | 113,145 | 124,116 |
| 23 | 35,172 | 41,638 | 57 | 75,624 | 84,733 | 91 | 114,268 | 125,289 |
| 24 | 36,415 | 42,980 | 58 | 76,778 | 85,950 | 92 | 115,390 | 126,462 |
| 25 | 37,652 | 44,314 | 59 | 77,931 | 87,166 | 93 | 116,511 | 127,633 |
| 26 | 38,885 | 45,642 | 60 | 79,082 | 88,379 | 94 | 117,632 | 128,803 |
| 27 | 40,113 | 46,963 | 61 | 80,232 | 89,591 | 95 | 118,752 | 129,973 |
| 28 | 41,337 | 48,278 | 62 | 81,381 | 90,802 | 96 | 119,871 | 131,141 |
| 29 | 42,557 | 49,588 | 63 | 82,529 | 92,010 | 97 | 120,990 | 132,309 |
| 30 | 43,773 | 50,892 | 64 | 83,675 | 93,217 | 98 | 122,108 | 133,476 |
| 31 | 44,985 | 52,191 | 65 | 84,821 | 94,422 | 99 | 123,225 | 134,642 |
| 32 | 46,194 | 53,486 | 66 | 85,965 | 95,626 | 100 | 124,342 | 135,807 |
| 33 | 47,400 | 54,776 | 67 | 87,108 | 96,828 | |||
| 34 | 48,602 | 56,061 | 68 | 88,250 | 98,028 | |||
Таблица 6.
Величины угла φ (в радианах) для разных процентных долей:
φ = 2 arcsin 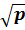
| % доля | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 | 0,000 0,063 0,089 0,110 0,127 0,142 0,155 0,168 0,179 0,190 | 0,020 0,066 0,092 0,111 0,128 0,143 0,156 0,169 0,180 0,191 | 0,028 0,069 0,094 0,113 0,130 0,144 0,158 0,170 0,182 0,192 | 0,035 0,072 0,096 0,115 0,131 0,146 0,159 0,171 0,183 0,193 | 0,040 0,075 0,098 0,117 0,133 0,147 0,160 0,172 0,184 0,194 | 0,045 0,077 0,100 0,118 0,134 0,148 0,161 0,173 0,185 0,195 | 0,049 0,080 0,102 0,120 0,136 0,150 0,163 0,175 0,186 0,196 | 0,053 0,082 0,104 0,122 0,137 0,151 0,164 0,176 0,187 0,197 | 0,057 0,085 0,106 0,123 0,139 0,153 0,169 0,177 0,188 0,198 | 0,060 0,087 0,108 0,125 0,140 0,154 0,166 0,178 0,189 0,199 |
| 1 2 3 4 5 6 7 8 9 10 | 0,200 0,284 0,348 0,403 0,451 0,495 0,536 0,574 0,609 0,644 | 0,210 0,291 0,354 0,408 0,456 0,499 0,539 0,577 0,613 0,647 | 0,220 0,298 0,360 0,413 0,460 0,503 0,543 0,581 0,616 0,650 | 0,229 0,304 0,365 0,418 0,465 0,507 0,547 0,584 0,620 0,653 | 0,237 0,311 0,371 0,423 0,469 0,512 0,551 0,588 0,623 0,657 | 0,246 0,318 0,376 0,428 0,473 0,516 0,555 0,592 0,627 0,660 | 0,254 0,324 0,382 0,432 0,478 0,520 0,559 0,595 0,630 0,663 | 0,262 0,330 0,387 0,437 0,482 0,524 0,562 0,599 0,633 0,666 | 0,269 0,336 0,392 0,442 0,486 0,528 0,566 0,602 0,637 0,670 | 0,277 0,342 0,398 0,446 0,491 0,532 0,570 0,606 0,640 0,673 |
| 11 12 13 14 15 16 17 18 19 20 | 0,676 0,707 0,738 0,767 0,795 0,823 0,850 0,876 0,902 0,927 | 0,679 0,711 0,741 0,770 0,798 0,826 0,853 0,879 0,905 0,930 | 0,682 0,714 0,744 0,773 0,801 0,828 0,855 0,881 0,907 0,932 | 0,686 0,717 0,747 0,776 0,804 0,831 0,858 0,884 0,910 0,935 | 0,689 0,720 0,750 0,778 0,807 0,834 0,861 0,887 0,912 0,937 | 0,692 0,723 0,752 0,781 0,809 0,837 0,863 0,889 0,915 0,940 | 0,695 0,726 0,755 0,784 0,812 0,839 0,866 0,892 0,917 0,942 | 0,698 0,729 0,758 0,787 0,815 0,842 0,868 0,894 0,920 0,945 | 0,701 0,732 0,761 0,790 0,818 0,845 0,871 0,897 0,922 0,947 | 0,704 0,735 0,764 0,793 0,820 0,847 0,874 0,900 0,925 0,950 |
| 21 22 23 24 25 26 27 28 29 30 | 0,952 0,976 1,000 1,024 1,047 1,070 1,093 1,115 1,137 1,159 | 0,955 0,979 1,003 1,026 1,050 1,072 1,095 1,117 1,140 1,161 | 0,957 0,981 1,005 1,029 1,052 1,075 1,097 1,120 1,142 1,164 | 0,959 0,984 1,007 1,031 1,054 1,077 1,100 1,122 1,144 1,166 | 0,962 0,986 1,010 1,033 1,056 1,079 1,102 1,124 1,146 1,168 | 0,964 0,988 1,012 1,036 1,059 1,082 1,104 1,126 1,148 1,170 | 0,967 0,991 1,015 1,038 1,061 1,084 1,106 1,129 1,151 1,172 | 0,969 0,993 1,017 1,040 1,063 1,086 1,109 1,131 1,153 1,174 | 0,972 0,996 1,019 1,043 1,066 1,088 1,111 1,133 1,155 1,177 | 0,974 0,998 1,022 0,045 1,068 1,091 0,113 1,135 1,157 1,179 |
| % доля | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 31 32 33 34 35 36 37 38 39 40 | 1,182 1,203 1,224 1,245 1,266 1,287 1,308 1,328 1,349 1,369 | 1,183 1,205 1,226 1,247 1,268 1,289 1,310 1,330 1,351 1,371 | 1,185 1,207 1,228 1,249 1,270 1,291 1,312 1,333 1,353 1,374 | 1,187 1,209 1,230 1,251 1,272 1,293 1,314 1,335 1,355 1,376 | 1,190 1,211 1,232 1,254 1,274 1,295 1,316 1,337 1,357 1,378 | 1,192 1,213 1,234 1,256 1,277 1,297 1,318 1,339 1,359 1,380 | 1,194 1,215 1,237 1,258 1,279 1,299 1,320 1,341 1,361 1,382 | 1,196 1,217 1,239 1,260 1,281 1,302 1,322 1,343 1,363 1,384 | 1,198 1,220 1,241 1,262 1,283 1,304 1,324 1,345 1,365 1,386 | 1,200 1,222 1,243 1,264 1,285 1,306 1,326 1,347 1,367 1,388 |
| 41 42 43 44 45 46 47 48 49 50 | 1,390 1,410 1,430 1,451 1,471 1,491 1,511 1,531 1,551 1,571 | 1,392 1,412 1,432 1,453 1,473 1,493 1,513 1,533 1,553 1,573 | 1,394 1,414 1,434 1,455 1,475 1,495 1,515 1,535 1,555 1,575 | 1,396 1,416 1,436 1,457 1,477 1,497 1,517 1,537 1,557 1,577 | 1,398 1,418 1,438 1,459 1,479 1,499 1,519 1,539 1,559 1,579 | 1,400 1,420 1,440 1,461 1,481 1,501 1,521 1,541 1,561 1,581 | 1,402 1,422 1,442 1,463 1,483 1,503 1,523 1,543 1,563 1,583 | 1,404 1,424 1,444 1,465 1,485 1,505 1,525 1,545 1,565 1,585 | 1,406 1,426 1,446 1,467 1,487 1,507 1,527 1,547 1,567 1,587 | 1,408 1,428 1,448 1,469 1,489 1,509 1,529 1,549 1,569 1,589 |
| 51 52 53 54 55 56 57 58 59 60 | 1,591 1,611 1,631 1,651 1,671 1,691 1,711 1,731 1,752 1,772 | 1,593 1,613 1,633 1,653 1,673 1,693 1,713 1,734 1,754 1,774 | 1,595 1,615 1,635 1,655 1,675 1,695 1,715 1,736 1,756 1,776 | 1,597 1,617 1,637 1,657 1,677 1,697 1,717 1,738 1,758 1,778 | 1,599 1,619 1,639 1,659 1,679 1,699 1,719 1,740 1,760 1,780 | 1,601 1,621 1,641 1,661 1,681 1,701 1,721 1,742 1,762 1,782 | 1,603 1,623 1,643 1,663 1,683 1,703 1,723 1,744 1,764 1,784 | 1,605 1,625 1,645 1,665 1,685 1,705 1,725 1,746 1,766 1,786 | 1,607 1,627 1,647 1,667 1,687 1,707 1,727 1,748 1,768 1,789 | 1,609 1,629 1,649 1,669 1,689 1,709 1,729 1,750 1,770 1,791 |
| 61 62 63 64 65 66 67 68 69 70 | 1,793 1,813 1,834 1,855 1,875 1,897 1,918 1,939 1,961 1,982 | 1,795 1,815 1,836 1,857 1,878 1,899 1,920 1,941 1,963 1,984 | 1,797 1,817 1,838 1,859 1,880 1,901 1,922 1,943 1,965 1,987 | 1,799 1,819 1,840 1,861 1,882 1,903 1,924 1,946 1,967 1,989 | 1,801 1,821 1,842 1,863 1,884 1,905 1,926 1,948 1,969 1,991 | 1,803 1,823 1,844 1,865 1,886 1,907 1,928 1,950 1,971 1,993 | 1,805 1,826 1,846 1,867 1,888 1,909 1,930 1,952 1,974 1,995 | 1,807 1,828 1,848 1,869 1,890 1,911 1,933 1,954 1,976 1,998 | 1,809 1,830 1,850 1,871 1,892 1,913 1,935 1,956 1,978 2,000 | 1,811 1,832 1,853 1,873 1,894 1,916 1,937 1,958 1,980 2,002 |
| 71 72 73 74 75 76 77 78 79 80 | 2,004 2,026 2,049 2,071 2,094 2,118 2,141 2,165 2,190 2,214 | 2,006 2,029 2,051 2,074 2,097 2,120 2,144 2,168 2,192 2,217 | 2,009 2,031 2,053 2,076 2,099 2,122 2,146 2,170 2,194 2,219 | 2,011 2,033 2,056 2,078 2,101 2,125 2,148 2,172 2,197 2,222 | 2,013 2,035 2,058 2,081 2,104 2,127 2,151 2,175 2,199 2,224 | 2,015 2,038 2,060 2,083 2,106 2,129 2,153 2,177 2,202 2,227 | 2,018 2,040 2,062 2,085 2,108 2,132 2,156 2,180 2,204 2,229 | 2,020 2,042 2,065 2,087 2,111 2,134 2,158 2,182 2,207 2,231 | 2,022 2,044 2,067 2,090 2,113 2,136 2,160 2,185 2,209 2,234 | 2,024 2,047 2,069 2,092 2,115 2,139 2,163 2,187 2,212 2,237 |
Окончание таблицы 6.
| % доля | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 81 82 83 84 85 86 87 88 89 90 | 2,240 2,256 2,292 2,319 2,346 2,375 2,404 2,434 2,465 2,498 | 2,242 2,268 2,294 2,321 2,349 2,377 2,407 2,437 2,469 2,501 | 2,245 2,271 2,297 2,324 2,352 2,380 2,410 2,440 2,472 2,505 | 2,247 2,273 2,300 2,327 2,355 2,383 2,413 2,443 2,475 2,508 | 2,250 2,276 2,302 2,330 2,357 2,386 2,416 2,447 2,478 2,512 | 2,252 2,278 2,305 2,332 2,360 2,389 2,419 2,450 2,482 2,515 | 2,255 2,281 2,308 2,335 2,363 2,392 2,422 2,453 2,485 2,518 | 2,258 2,284 2,310 2,338 2,366 2,395 2,425 2,456 2,488 2,522 | 2,260 2,286 2,313 2,341 2,369 2,398 2,428 2,459 2,491 2,525 | 2,263 2,289 2,316 2,343 2,372 2,401 2,231 2,462 2,495 2,529 |
| 91 92 93 94 95 96 97 98 99,0 | 2,532 2,568 2,606 2,647 2,691 2,739 2,793 2,858 2,941 | 2,536 2,572 2,610 2,651 2,295 2,744 2,799 2,865 2,942 | 2,539 2,575 2,614 2,655 2,700 2,749 2,805 2,872 2,943 | 2,543 2,579 2,618 2,659 2,705 2,754 2,811 2,880 2,944 | 2,546 2,583 2,622 2,664 2,709 2,760 2,818 2,888 2,945 | 2,550 2,587 2,626 2,668 2,714 2,765 2,824 2,896 2,946 | 2,554 2,591 2,630 2,673 2,719 2,771 2,830 2,904 2,948 | 2,557 2,594 2,634 2,677 2,724 2,776 2,837 2,913 2,949 | 2,561 2,598 2,638 2,681 2,729 2,782 2,844 2,922 2,950 | 2,564 2,602 2,642 2,686 2,734 2,788 2,851 2,931 2,951 |
| 99,1 99,2 99,3 99,4 99,5 99,6 99,7 99,8 99,9 100 | 2,952 2,963 2,974 2,987 3,000 3,015 3,032 3,052 3,078 3,142 | 2,953 2,964 2,975 2,988 3,002 3,017 3,034 3,054 3,082 | 2,954 2,965 2,976 2,989 3,003 3,018 3,036 3,057 3,085 | 2,955 2,966 2,978 2,990 3,004 3,020 3,038 3,059 3,089 | 2,956 2,967 2,979 2,992 3,006 3,022 3,040 3,062 3,093 | 2,957 2,968 2,980 2,993 3,007 3,023 3,041 3,064 3,097 | 2,958 2,969 2,981 2,995 3,009 3,025 3,044 3,067 3,101 | 2,959 2,971 2,983 2,996 3,010 3,027 3,046 3,069 3,107 | 2,960 2,972 2,984 2,997 3,012 3,028 3,048 3,072 3,113 | 2,961 2,973 2,985 2,999 3,013 3,030 3,050 3,075 3,122 |
Таблица 7.
Критические значения коэффициента корреляции rxy Пирсона
| k=n-2 | p | k=n-2 | p | ||
| 0 ,05 | 0,01 | 0,05 | 0,01 | ||
| 5 | 0,75 | 0,87 | 27 | 0,37 | 0,47 |
| 6 | 0,71 | 0,83 | 28 | 0,36 | 0,46 |
| 7 | 0,67 | 0,80 | 29 | 0,36 | 0,46 |
| 8 | 0,63 | 0,77 | 30 | 0,35 | 0,45 |
| 9 | 0,60 | 0,74 | 35 | 0,33 | 0,42 |
| 10 | 0,58 | 0,71 | 40 | 0,30 | 0,39 |
| 11 | 0,55 | 0,68 | 45 | 0,29 | 0,37 |
| 12 | 0,53 | 0,66 | 50 | 0,27 | 0,35 |
| 13 | 0,51 | 0,64 | 60 | 0,25 | 0,33 |
| 14 | 0,50 | 0,62 | 70 | 0,23 | 0,30 |
| 15 | 0,48 | 0,61 | 80 | 0,22 | 0,28 |
| 16 | 0,47 | 0,59 | 90 | 0,21 | 0,27 |
| 17 | 0,46 | 0,58 | 100 | 0,20 | 0,25 |
| 18 | 0,44 | 0,56 | 125 | 0,17 | 0,23 |
| 19 | 0,43 | 0,55 | 150 | 0,16 | 0,21 |
| 20 | 0,42 | 0,54 | 200 | 0,14 | 0,18 |
| 21 | 0,41 | 0,53 | 300 | 0,11 | 0,15 |
| 22 | 0,40 | 0,52 | 400 | 0,10 | 0,13 |
| 23 | 0,40 | 0,51 | 500 | 0,09 | 0,12 |
| 24 | 0,39 | 0,50 | 700 | 0,07 | 0,10 |
| 25 | 0,38 | 0,49 | 900 | 0,06 | 0,09 |
| 26 | 0,37 | 0,48 | 1000 | 0,06 | 0,09 |
Таблица 8.
Таблица 9.
Число
Степеней
Свободы
К
p
Число
Степеней
Свободы
К
p
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная литература:
1. Ермолаев О. Ю. Математическая статистика для психологов / О. Ю. Ермолаев. – М.: Московский психолого-социальный институт, Флинта, 2003. – 336 с. (Библиотека УлГПУ; Электронный ресурс. – Режим доступа: http://www/pedlib.ru).
2. Сидоренко Е. В. Методы математической обработки в психологии / Е.В. Сидоренко. - СПб.: Речь, 2001. - 349 с. (Библиотека УлГПУ).
Дополнительная литература:
1. Годин А. М. Статистика: учеб. для вузов / А. М. Годин. - М.: Дашков и К°, 2009. - 457 с. (Библиотека УлГПУ).
2. Математическая психология: Школа В. Ю. Крылова. – М.: Институт психологии РАН, 2010. – 503 с. (Электронный ресурс. – Режим доступа: http://www/knigafund.ru).
3. Романко В. К. Статистический анализ данных в психологии: учебное пособие / В. К. Романко. – М.: БИНОМ. Лаборатория знаний, 2012. – 313 с. (Электронный ресурс. – Режим доступа: http://www/knigafund.ru).
4. Туганбаев А. А. Задачи по высшей математике для психологов: учеб. пособие для вузов / А. А. Туганбаев. - М.: Флинта: МПСИ, 2008. - 319 с. (Библиотека УлГПУ).
5. Суходольский Г. В. Математическая психология / Г.В. Суходольский. - Харьков: Гуманитарный центр, 2006. - 358 с. (Библиотека УлГПУ).
Подписано в печать ______________ Формат 60х90 1/16
Бумага офсетная Заказ № ______
Печать оперативная Тираж 500
Усл. печ. л. 4,2
Ротапринт Ульяновского государственного педагогического университета имени И. Н. Ульянова
432700 г. Ульяновск, пл. 100-летия со дня рождения В. И. Ленина, 4
МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
Учебно-методическое пособие
Ульяновск
2017
Дата: 2019-02-02, просмотров: 1435.