Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Теорема 1

Если функция ¦(x,y) непрерывна в замкнутой области s, ограниченной линиями:                                       x=a, x=b (a<b),

                                                   y=j(x), y=Y(x);

где j (x) и Y(x) непрерывны на [a,b], причем j(x)£Y(x), то имеет место равенство:

 

(1)

позволяющее вычисление двойного интеграла свести к последовательному вычислению определенного интеграла от определенного интеграла (или к вычислению повторного интеграла)

Доказательство:

Разобьем область s на n частей, путем проведения прямых параллельных OY и n кривых, заданных уравнениями

y=j₀(x), y=j₁(x)¼y=j_n(x),

где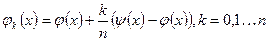

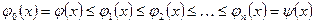
Пусть 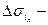 область деления, для которой

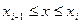
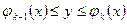
Пусть m_ik – наименьшее, значения функции ¦(x,y) в области s,

    а М_ik – наибольшее значения функции ¦(x,y) в области s.

Так как Ds_ik – замкнутая область, то эти значения принимаются в некоторой области Ds_ik причем

 

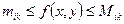
проинтегрируем по y это неравенство для каждого значение x:

 

 

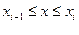
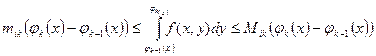   (2)

Проинтегрируем (2) по x в пределах x_i-1 до x_i и учитывая, что

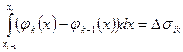 - площадь области Ds_ik

получаем:

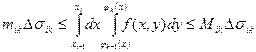   (3)

(3) имеют место в каждой области деления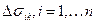

                                                                              

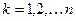
Просуммируем по k от 1 до n

,

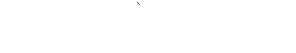так как

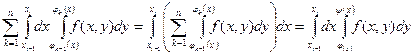
Суммируя по i: i=1, до n

или

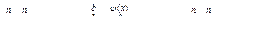                                        (4)

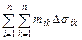- нижняя интегральная сумма функции f(x,y),

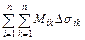- верхняя интегральная сумма функции f(x,y).

8

Пусть n®¥,l®0, так как функция ¦(x,y) по условию интегрируема в области s, то при l®0 эти суммы имеют общий предел:

 

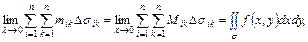
а это означает из (4):

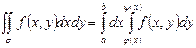
Теорема 2

Если функция ¦(x,y) непрерывна в замкнутой области s, ограниченной линиями y= c, y= d ( c < d); x= Ф( y), x= y( y), Ф( y) и y( y) – непрерывны на [c,d], причем, Ф( y) £ y( y), то

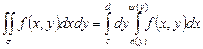(5)

При вычислении двойного интеграла по формуле (5) вначале вычисляется 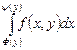 при y=const (c£y£d) в пределах изменения х (для области s), затем полученная функция от y интегрируется по y в максимальных пределах изменения у для области s.

 

Пример

Вычислить 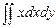  по области s: y=-x, y=1, y=x²

Для вычисления двойного интеграла нужно привести его к повторному интегралу

1. Привести к повторному интегралу 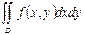, где область D

D: y=0, y=x, x=3.

1) спроектировать D на OX: 0£x£3 - пределы внешнего интеграла;

2) возьмем в этих пределах произвольную точку х;

3) прострелим область D стрелкой перпендикулярной 0Х, проходящую через выбранную точку х;

4) укажем место входа и выхода стрелки из области D (точка А и точка В);

 

 

5) из уравнений линий , на которых лежат А и В

y_А £ y £ y_В

получим пределы внутреннего интеграла:

0 £ y £ x

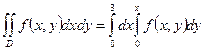
2. Расставить пределы интегрирования в двойном интеграле ,где область D задана уравнениями

D: y=0, y=x², x+y=2

Разобъем область D на две области D₁ и D₂ :

                     D₁: 0£x<1, 0£y£x²

                     D₂: 1£x£2, 0£y£2-x

Примеры вычисления двойных интегралов

1. Найти 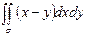 по области s,

заданной уравнениями:

y=0,y=x², x=2

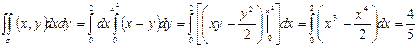
2. Вычислить двойной интеграл 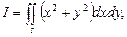 где S(0£x£1, 0£y£1)

Расставляя пределы интегрирования будем иметь

Геометрически:

объем цилиндра с квадратным нижним основанием, ограниченного сверху параболоидом вращения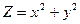

3. Вычислить двойной интеграл

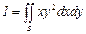, где S (0£x£1;-2£y£3).

 Расставляя пределы интегрирования и разделяя переменные, будем иметь:

 

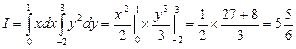
4. Вычислить двойной интеграл по прямоугольнику S, ограниченному прямыми x=2, x=5, y=1, y=3.

Можно интегрировать и в обратном порядке:

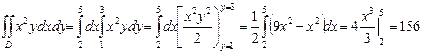
5. Вычислить 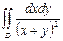, по области D, ограниченной линиями:

3£x£4, 1£y£2

 

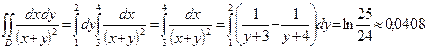
6. Вычислить 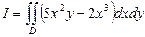, где область D ограничена линиями: x=0, x=1; y=0, y=3/2.

 

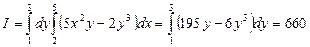
7. Вычислить 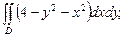гдеобласть D огранирчена линиями:

 x=0, y=0, y=3/2

 

 

 

 

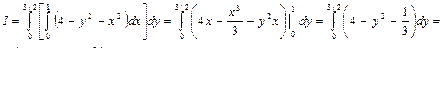
8.  Вычислить 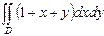, где область D: ограничена линиями:

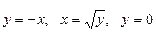
9. Вычислить 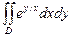 по области D

 D:- треугольник, ограниченный прямыми

y=x,y=0,x=1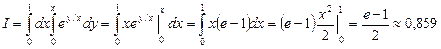

10. Вычислить 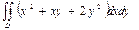, D: - треугольник, ограниченный осями координат и прямой y=-x+1. Тогда

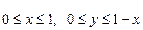
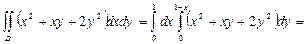
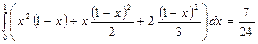
или иначе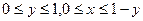

                                  

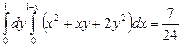
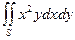11. Вычислить по области S

 S - треугольник с вершинами

О(0,0), А(2,0), В(2,1).

Тогда область S ограничена прямыми

y=0, y=x/2, x=2

 

Иначе

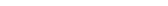
12. Вычислить площадь области D, ограниченной параболой y²=2x и хордой, соединяющей точки (2,-2) и (8,4). Прямая x=2 разбивает область D на две нормальные ограниченные неравенствами:

Или область D рассматривать как область нормальную

 

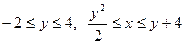
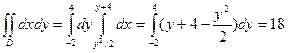
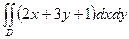13. Вычислить , по области D, ограниченый трегольником с вершинами

(-1,-1), (2,-4), (1,3).

Составим уравнения прямых:

 

при помощи прямой x=1 разобьем треугольник на две нормальные области

Аналогично: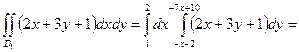

 

Окончательно

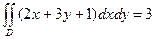
Чтобы найти среднее значение 2x+3y+1, надо значение двойного интеграла разделить на площадь треугольника, которая равняется 9. Для среднего значения получим число равное 1/3