Задача интегрирования принципиально труднее задачи дифференцирования. В дифференциальном исчислении имелись конструктивные определения производной и ряд теорем, дающих правила дифференцирования суммы, произведения, сложных функций.
В интегральном исчислении определение не конструктивно, правил для интегрирования произведения, частного, сложной и обратной функции нет. Имеются лишь отдельные приемы, методы, позволяющие интегрировать отдельные классы функций. Наиболее важными методами являются: метод разложения, метод подстановки и метод интегрирования по частям.
Метод разложения
Пусть f(x) = fi(x) + £г(х), тогда на основании свойства 6:
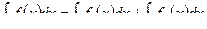
По возможности fj(x) и f2(x) подбираются так, чтобы интеграл от каждой из функций находился непосредственно.
Пример 2
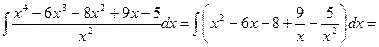
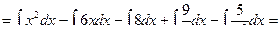
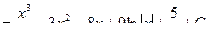
Пример 3
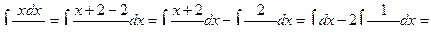
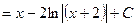
Метод подстановки (или замена переменной)
Пусть требуется найти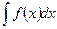 
, причем непосредственно интеграл найти не можем: но нам известно, что первообразная для функции 
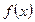существует, сделаем замену 
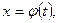где 
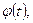непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда
dx=φ'(t)dt.
Докажем, что
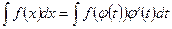
Производная от левой части равна
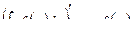
Производная от правой части – производная сложной функции, где t – промежуточный параметр.
Учитывая, что 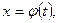, тогда 
, 
 |
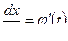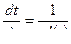
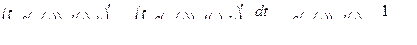
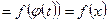
Следовательно, производные по х от правой и левой частей равны.
Замечание. Иногда целесообразно применить замену переменной в виде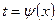 
, а не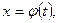
Пример 4
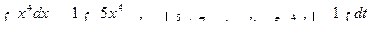
6
Пример 5
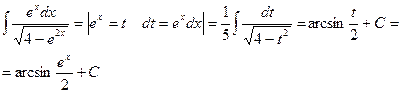
Пример 6
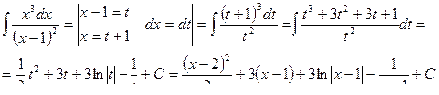
Пример 7
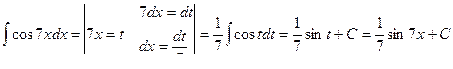
Пример 8
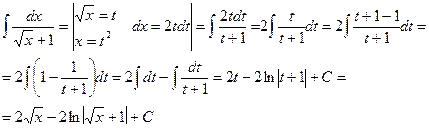
Интегрирование по частям
Пусть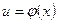 
и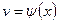 
– непрерывные дифференцируемые функции, тогда
d(u·v) = du · v + u · dv,
интегрируя, получим
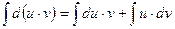
или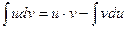 
Формула интегрирования по частям применяется к интегрированию выражений, которые можно представить в виде произведения двух сомножителей u и dv.
Пример 9
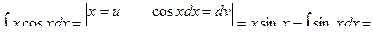
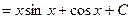
К интегрированию по частям относятся случаи, когда в подынтегральное выражение входят:
a) произведение функций
Р(х)атх ;
Р(х)етх ;
Р(х) sinαх;
P(x)cosax, где Р(х) – многочлен n-степени
b) логарифмические функции;
с) обратные тригонометрические функции;
d) некоторые другие функции.
Чтобы применить формулу интегрирования по частям, надо все подынтегральное выражение разбить на два множителя, один из которые обозначить u , а другой dv. При этом:
1. dx должен быть отнесен к dv,
2. dv, должен быть таким, чтобы интегрированием можно было легко найти v, так как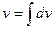 
(константу не добавлять)..
3. для случаев, перечисленных в пунктах а , b, с d, можно пользоваться следующим правилом: за u надо брать такую функцию из подынтегрального выражения, которая при дифференцировании упрощается, и остальная часть – имеет известный интеграл.
ex ex
sinax dx u = P(x) dv= sinax dx
cosax cosax
ax ax
Замечание. Формула интегрирования по частям применяется столько раз, какова степень многочлена Р(х).
II arcctgmαx arcctgmαx
arccosmαx arccosmαx
arcsinm α x dx u= arcsinm α x dv = P( x) dx
arctgmαx arctgmαx
lnmαx lnmαx
III возможен любой выбор сомножителей
sinbx
cosbx dx
IV возможен любой выбор сомножителей
sin(lnx) sin(lnx
cos(lnx) dx u = cos(lnx) dv = dx
Замечание. После двукратного применения формулы интегрирования по частям в интегралах вида IV, V возникает заданный первоначально интеграл. В этом случае мы приходим к линейному уравнению относительно искомого интеграла.
Пример 10
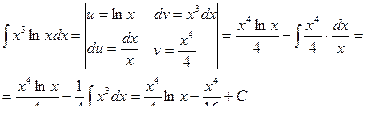
Пример 11
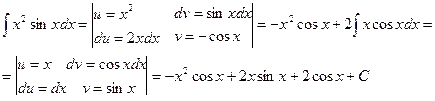
Пример 12
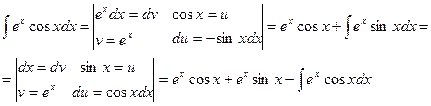
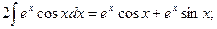
Пример 13
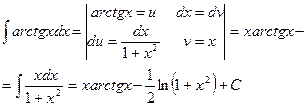
Пример 14
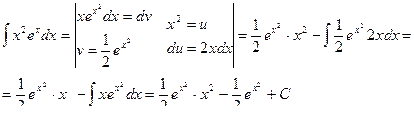
Дата: 2018-12-28, просмотров: 246.
