Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Интегрирование рациональных дробей

Рациональной дробью называется дробь 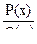, числитель и знаменатель которой являются многочленами.

Дробь называется правильной если степень числителя меньше степени знаменателя. В противном случае, дробь – неправильная.

Всякую неправильную дробь (рациональную) можно представить в виде суммы многочлена и правильной дроби. Для этого необходимо числитель разделить на знаменатель, как многочлен на многочлен. Сумма простейших дробей равна правильной дроби.

Справедливо и обратное: всякую правильную рациональную дробь P(x)/Q(x) можно представить в виде суммы простых дробей. Для этого надо знаменатель Q(x) разложить на множители.

Теорема. Всякий многочлен Q(x) с действительными коэффициентами можно разложить на действительные многочлены первой и второй степени (х-а),... (х-а) ^k (x²+px+q),... (х²+px+q), (1)

Пусть Q(x)= х ⁿ+А₁ x^{n - l}+...+An. Приравняем его к нулю, получим уравнение n-степени. Оно имеет n корней. a¹, а², …, аⁿ

Зная корни, можно разложить Q(x) на множители Q(x)=(x-a₁) ... (х-а _n).

1. Если корни многочлена Q(x) действительные и разные, то

2. Если среди корней многочлена есть равные действительные корни, тогда, объединив множители, соответствующие одинаковым корням, получим

3. Если среди корней многочлена есть комплексные

a₁= α + β i, a₂= α – β i, тогда

(х – a₁)(х – a₂) = (x – α + β i)(x – α – β i)=(x – a)² – (β i)²=

= х² – 2α x + α²+β²= x²+ px + q (ввели обозначения –2α x= p и α²+β² = q). Объединяя множители, соответствующие попарно сопряженным корням, получим множители вида x²+px+q с действительными коэффициентами. Итак, многочлен Q(x) можно разложить на многочлены первой и второй степени.

Пусть P(x)/Q(x) - правильная рациональная дробь. Разложим Q(x) на действительные множители. Они имеют вид

(х-а), …, (х-а)^л, (x²+px+q), …, (x²+px+q)^k.

Теорема. При разложении правильной рациональной дроби P(x)/Q(x) на сумму простых дробей каждому множителю многочлена Q(x) вида (х-а) соответствует дробь А/(х-а), каждому множителю знаменателя вида (х-а) ^k соответствует сумма k дробей А₁/(х-а) + А₂/(х-а)²+ ...+ А_k/(х-а)^k. Каждому множителю вида х+px+q соответствует дробь – 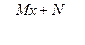, а множителю вида (х+px+q)^k соответствует сумма дробей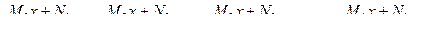

 

Определение. Правильные рациональные дроби вида:

                                          

 

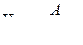(k – целое; k≥2)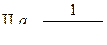          

 

             

 

 

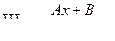
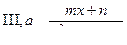
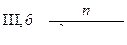
называются простейшими (элементарными) дробями I, IL, III и IV типов. Рассмотрим интегралы от простейших дробей:

 

 

 

 

 

 

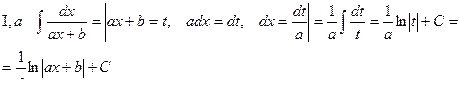
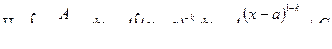
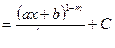
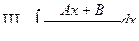
При делении числителя и знаменателя дроби на коэффициент, стоящий при х² (С≠1), интеграл сводится к интегралу вида

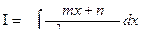
Здесь различаются три случая:

 

 

1. Корни знаменателя действительные и равные, т е.

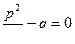
Тогда x²+px+q = (х – х₁)² и интеграл сводится к интегралу вида

,

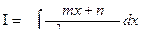который решается следующим образом. Сделаем подстановку x - x₁=t и решим.

Пример 15

 

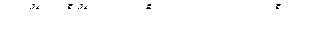
2. Корни знаменателя мнимые, т.е.

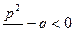
В этом случае подынтегральная функция разбивается на два слагаемых, причем, в первом из них числитель выделяется в виде половины производной знаменателя, а во втором - знаменатель приводится к сумме квадратов:

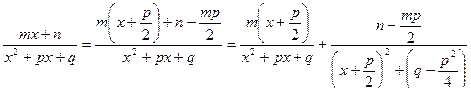
Этим приемом заданный интеграл разбивается на два интеграла:

 

 

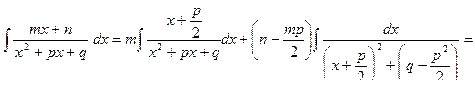
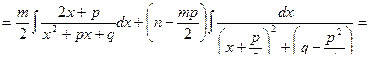
Пример 16

 

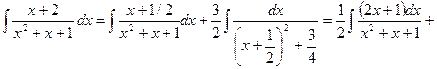
3. Корни знаменателя действительные и разные, т е.

                    , тогда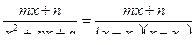

 

и полученная дробь раскладывается на две простейшие дроби:

       где А, В - неопределенные коэффициенты.

Числители этих простейших дробей находятся методом неопределенных коэффициентов. Суть метода заключается в том, что левую и правую части формулы разложения приводят к общему знаменателю. Его отбрасывают. Сравнивают коэффициенты при одинаковых степенях x в левой и правой частях.

 

;

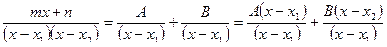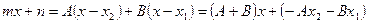
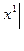
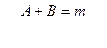
 Пример 17

 

 

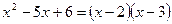
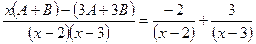
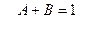
       A = – 2  B = 3

 

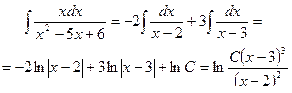
Замечание. Основной прием вычисления интеграла III вида - это дополнение квадратного трехчлена Cx²+dx+e до полного квадрата (при этом предполагается, что квадратный трехчлен не является точным квадратом). После этого, если А=0 , то интеграл Ш сводится к интегралу

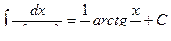
или

 

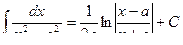
Если А≠0, то решение – как предыдущее.

IV.

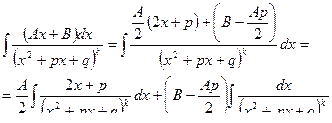
I интеграл

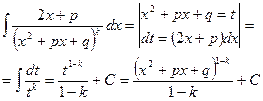
II интеграл

 

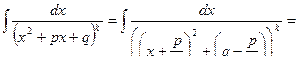
Преобразуем

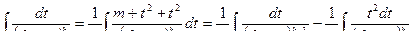
Рассмотрим

 

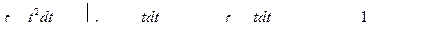
Подставим найденное значение в интеграл:

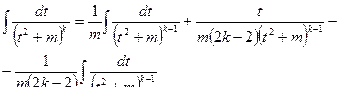
приведя подобные интегралы, получим:

 

( + )

Получившееся равенство позволяет 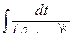 выразить через

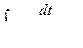, то есть понизить степень знаменателя в подынтегральном выражении на единицу. Применяя полученную формулу (k-1) раз, придем к табличному интегралу. Формула ( + ) называется рекуррентной

 

Пример 18

 

 

 

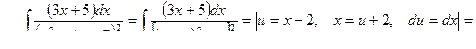
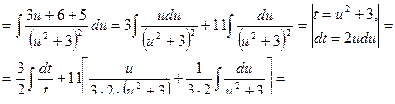
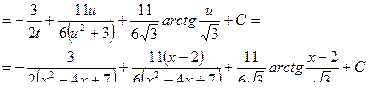
Обобщая результаты, заключаем, что всякая рациональная дробь может быть проинтегрирована в элементарных функциях.

 

Общее правило для интегрирования рациональных функций

Для того, чтобы проинтегрировать рациональную функцию (рациональную дробь), надо:

1. Если рассматриваемая дробь 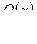неправильная, то выделить из нее целую часть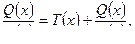

где T( x) – многочлен,

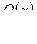 – правильная рациональная дробь.

2. Правильную рациональную дробь 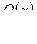представить в виде суммы элементарных дробей по схеме следующей теоремы:

Теорема.  Если 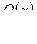 – правильная рациональная дробь, где

Р(х) – произведение линейных и квадратичных множителей:

Р(х) = (х-а)²... (x-b)²... (x2+px+q)^λ..(x2+px+q)^μ, то эта дробь может быть разложена на элементарные дроби по следующей схеме:

 

 

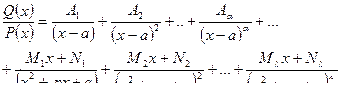
3. Представить интеграл от данной дроби в виде суммы интегралов от целой части и от соответствующих элементарных дробей.

Таким образом, интеграл любой рациональной функции может быть выражен через элементарные функции:

1) через логарифмы – в случае простейших дробей типа I;

2) через рациональные функции – в случае простейших дробей типа II;

3) через логарифмы и арктангенсы – в случае простейших дробей типа III:

4) через рациональные функции и арктангенсы – в случае простейших дробей типа IV.

Пример 19.

 

 

=

 

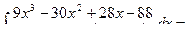
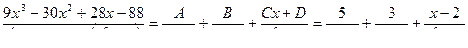
  A = 5; B = 3; C = 1; D = 2

Пример 20.

=

 

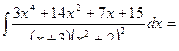
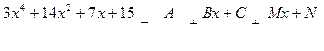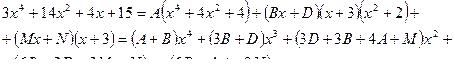
         A = 1

B = 0

D = 1

M = 2

N = 0

 

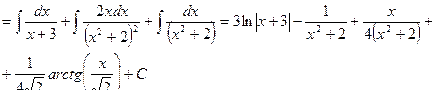
Пример 21.

 

 

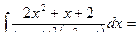
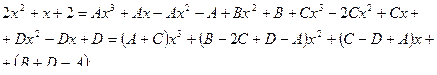
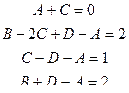
Пример 22.

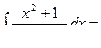
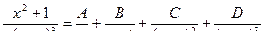
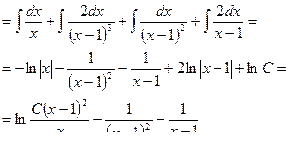
Интегрирование иррациональных функций

Не от любой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим лишь те случаи, когда это удается сделать.

Теорема 1. Интеграл вида ,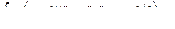

где R(…) – рациональная функция своих аргументов, подстановкой 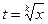  приводится к интегралу от рациональной функции.

Действительно, пусть k – общий знаменатель m/n, p/q, …, r/s.

Сделаем подстановку 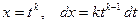, тогда и каждая дробная степень выразится через целую степень t , и следовательно, подынтегральная функция преобразуется в рациональную

функцию от t

 

Пример 23

Теорема 2. Интеграл вида 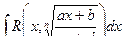, подстановкой  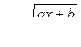 приводится к интегралу от рациональной функции.

Доказательство.

Пусть ;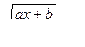

;

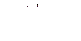
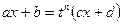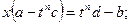
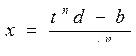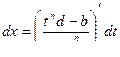
Следовательно,

Следствие. Если под знаком интеграла стоит ,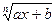

то с помощью подстановки 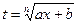   интеграл вида  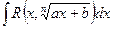приводится к интегралу от рациональной функции.

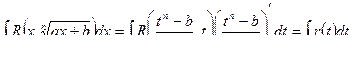
где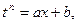

 

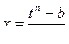
Пример 24

 

 

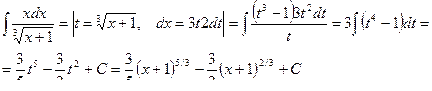
Следствие 2. Интеграл вида 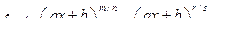, с помощью подстановки ,

где k – общий знаменатель m/n, r/s приводится к интегралу от

рациональной функции.

 

Пример 25

 

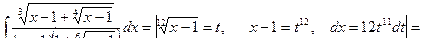
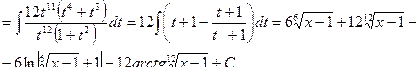
Пример 26

 

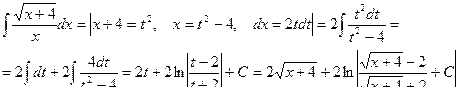
Теорема 3.  Вычисление интегралов вида

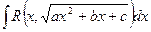
сводится к вычислению интегралов следующих трех типов:

I.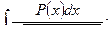

 

II. 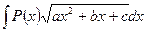, где P( x) – многочлен степени n

III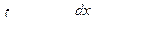

Покажем, что интегралы ІІ и ІІІ типов могут быть сведены к интегралу І типа.

 

ІІ тип:

 

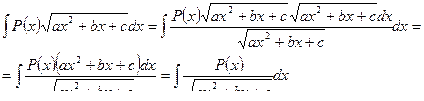
(т.е. для преобразования интеграла ІІ типа достаточно подынтегральную функцию разделить и умножить на )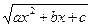

Для приведения интеграла ІІІ к интегралу типа І применяют так называемую «обратную» подстановку

 

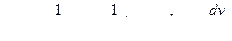
ІІІ тип:

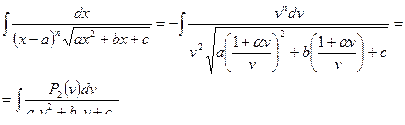
где a₁, b₁, c₁  – коэффициенты трехчлена, подученные после приведения подобных членов

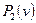 – многочлен.

Теорема 4.

  ( * )

где Q( x) – многочлен с неопределенными коэффициентами, степень которого ниже степени многочлена P( x);

λ– произвольная константа;

При вычислении указанного вида интегралов применяется

метод неопределенных коэффициентов

Для нахождения неопределенных коэффициентов

дифференцируют обе части равенства (*), затем умножают на 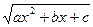и, сравнивая коэффициенты при одинаковых степенях х, определяют λ и коэффициенты многочлена Q(x).

Замечание. Формулу (*) применяют тогда, когда степень многочлена Р(х)больше единицы.

Пример 27.

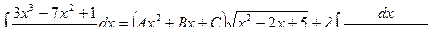
Продифференцируем это равенство:

Приведем к общему знаменателю и перемножим:

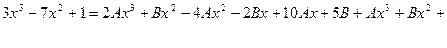
Найдем коэффициенты с помощью метода неопределенных коэффициентов:

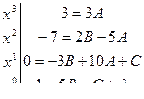
A = 1, B = -1, C = -13,  λ = -7

Подставим найденные значения коэффициентов и получим интеграл от элементарной функции

Пример 28

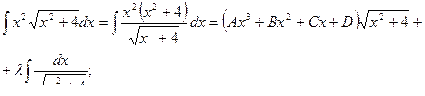
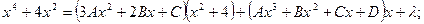
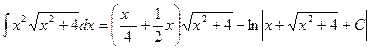
Пример 29

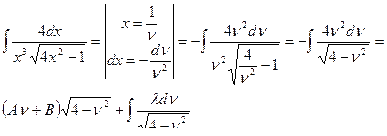
Теорема 5. Интеграл вида 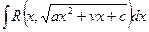с помощью

подстановок Эйлера приводится к интегралу от рациональной

функции.

Подстановка Эйлера:

1. Если а > 0 , то используется подстановка

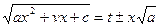
2. Если а < 0, с>0, то используется подстановка

 

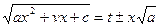
3. Если а < 0, а. подкоренное выражение раскладывается на действительные множители , то используется подстановка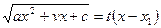

 

Пример 30

 

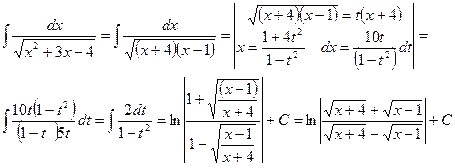
Интегрирование дифференциальных биномов.

 

Дифференциальным биномом называется выражение x^m (а + bх ⁿ) ^p dx, где m, n, p – рациональные числа.

Теорема. Интеграл от дифференциального бинома 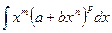приводится к интегралу от рациональной функции лишь в трех случаях:

1) р – целое число, то с помощью подстановки ,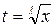

где λ – общий знаменатель m и n

2)      целое число, то с помощью подстановки

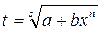, где s - знаменатель р;

3) 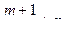 – целое число, то с помощью подстановки

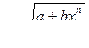, где s – знаменатель р.

Академик П.Л.Чебышев (1821-1894) доказал: что во всех остальных случаях интеграл от дифференциального бинома через элементарные функции не выражается.

 

Пример 31.

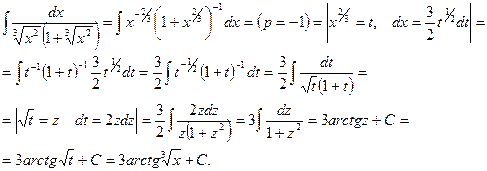
Пример 32

.

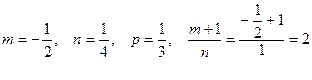
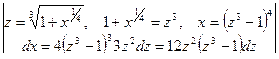– подстановка

 

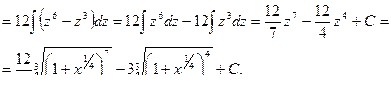
Интегрирование тригонометрических функций.

 

Переходя к рассмотрению приемов интегрирования тригонометрических выражений, предварительно заметим, что любая тригонометрическая функция рационально выражается через тангенс половинного угла:

 

      ( 1 )

 

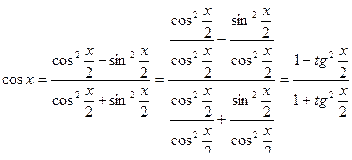         ( 2 )

 

а так как tgx, ctgx, secx, cosecx рационально выражаются через

sinx и cosx , то они рационально будут выражаться и через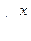

Теорема 1. Интеграл вида 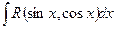подстановкой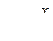

приводится к интегралу от рациональной функции t, который, как было указано выше, всегда выражается в элементарных функциях.

Действительно, пусть 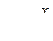, тогда на основании (1), (2)

    

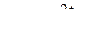
Определим x и dx, найдем, что     

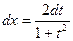
В подынтегральное выражение вместо sinx, cosx и dx подставим их значения

,

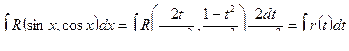где r(t) - рациональная функция t.

Так как подстановкой интеграл от любой рациональной

относительно sinx и cosx, тригонометрической функции приводится к

интегралу от рациональной функции , то подстановка 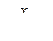называется универсальной.

 

Пример 33.

Замечание. Универсальная подстановка всегда приводит к цели, однако часто она приводит к громоздким выкладкам

Рассмотрим другие подстановки, которые в частных случаях быстрее приводят к цели.

Теорема 2. Если функция R(sinx, cosx) нечетна относительно cosx , то интеграл  подстановкой t = sinx приводится к интегралу от рациональной функции.

Действительно, преобразуем интеграл

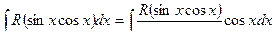
Так как R(sinx,cosx) нечетна относительно cosx и может содержать cosx лишь в четных степенях. Следовательно, это выражение является рациональной функцией относительно sinx:

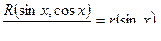  то есть

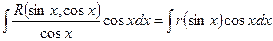
К последнему интегралу применим подстановку t = sinx, тогда dt=cosxdx:

=

Таким образом, указанная подстановка привела данный интеграл к интегралу от рациональной функции относительно t.

 

 

Пример 34.

 

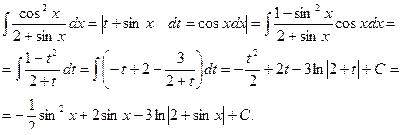
Теорема 3. Если функция R(sinx,cosx) нечетна относительно sinx ,то подстановкой t = cosx интеграл риводится к интегралу от рациональной функции.

Пример 35.

 

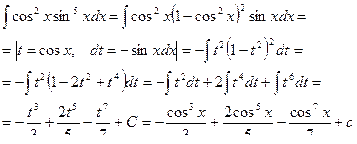
Пример 36.

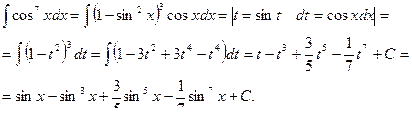
Замечание. Теоремы 2 и 3 применяются при интегрировании произведения sin^m cos ⁿ x натуральных степеней cosx и sinx, когда хотя бы одно из чисел m и n - нечетное.

 

Теорема 4. Если функция R(sinx,cosx) имеет четный характер

относительно sinx и cosx . то интеграл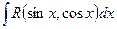

подстановкой t = tgx приводится к интегралу от рациональной функции.

Преобразуем подынтегральную функцию:

                    R(sinx,cosx) = R(tgx cosx, cosx)

Правая часть этого равенства имея четный характер относительно cosx, может содержать лишь четные степени cosx , а т. к.

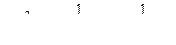
то вся подынтегральная функция является некоторой рациональной функцией от tgx, т.е. R(sinx,cosx)=r(tgx).

Умножим и разделим r(tgx) на sec²x и затем применим подстановку

t = tgx, dt = sec²xdx

Получим

Заметим также, что cos² x и sin ² x могут быть рационально выражены через tg²x:

 

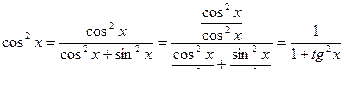
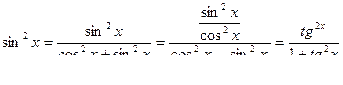
Пример 37.

 

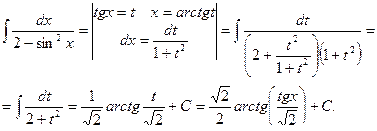
Теорема 5. Если подынтегральная функция представлена в виде произведения неотрицательных степеней sinx  и cosx, то интегрирование таких функций производят заменяя четные степени sinx и cosx синусами и косинусами кратных аргументов, используя при этом известные формулы тригонометрии

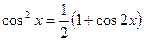
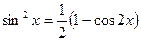
Пример 38.

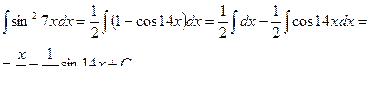
Пример 39.

Пример 40.

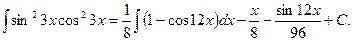
Примечание 1. Для интегралов от целых, больших единицы, степеней tgx, сtgx и от положительных четных степеней secx и cosecx

удобнее использовать соотношения:

  

 

 

 

Пример 41.

 

 

Пример 42.

 

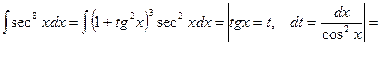
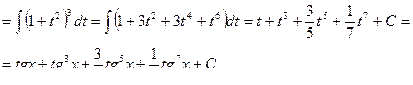
Примечание 2. Интегралы произведения синусов и косинусов различных аргументов приводятся к табличным интегралам с помощью тригонометрических формул:    

 

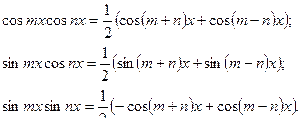
То есть

Пример 43.

 

 

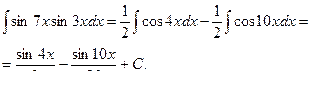
Пример 44.

 

 

Интегрирование иррациональных функций с помощью тригонометрических подстановок

Квадратный трехчлен, стоящий под знаком интеграла, путем выделения полного квадрата и замены переменных может быть представлен в форме двучлена 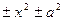  и тогда интеграл вида

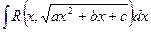
где R(...) – рациональная функция, всегда можно свести к одному из интегралов следующих типов:

1.

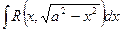
2.

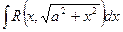
3.

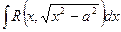
.    4. Четвертая комбинация знаков (- x₂-а₂) приводит нас к

подынтегральной функции, которая не существует в действительной области.

Теорема 1. Интеграл вида 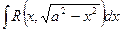подстановкой х=а sint (х=а cost) сводится к интегралу от рациональной функции относительно sint и cost.

. Действительно, пусть х=а sint, тогда dx = a cost dt,

 

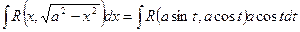
Пример 45.

 

Теорема 2. Интеграл вида 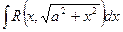 подстановкой

x=a tgt сводится к интегралу от рациональной функции относительно tgt и sect.

Действительно, пусть x=a tgt, тогда dx=a sec²tdt,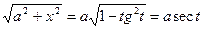

 

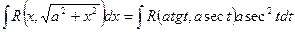
Пример 46.

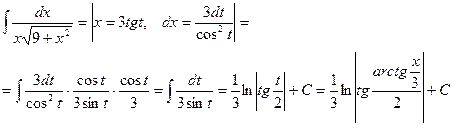
Теорема 3. Интеграл вида 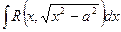 подстановкой

x=a seсt сводится к интегралу от рациональной функции относительно tgt и sect.

Действительно, пусть x=a sect, тогда dx=a tgt sect dt,

 

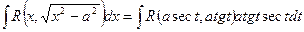
Пример 47.

 

Пример 48

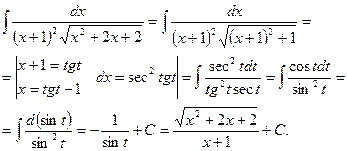
Понятие о “неберущихся” интегралах

Теорема существования неопределенного интеграла утверждает, что всякая непрерывная на интервале (а, b) функция f(x) имеет на этом интервале первообразную F(x). Эта теорема вовсе не утверждает: что первообразную данной функции можно фактически отыскать с помощью конечного числа известных операций и выразить ответ в элементарных функциях (алгебраических, показательных, тригонометрических и т.п.). Более того, имеются такие элементарные функции, интегралы от которых не выражаются через элементарные функции.

Так, например, мы уже указывали, что первообразные от дифференциальных биномов, не принадлежащие к трем рассмотренным видам (условия Чебышева), не выражаются через элементарные функции в конечном виде.

Такие интегралы называют “неберущимися”, подразумевая под этим, что такого рода интегралы не могут быть выражены с помощью конечного числа элементарных функций.

Интегралы вида

,

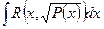где Р(х) – многочлен степени выше второй, в общем случае не выражается через элементарные функции. При этом, если Р(х) - многочлен третьей или четвертой степени, то такие интегралы

называются эллиптическими, если же степени выше четвертой, то ультраэллиптическими.

В некоторых случаях 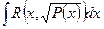могут выражаться и через элементарные функции, имеющие большое прикладное значение; следует. указать интеграл Пуассона: 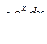; интегральный синус 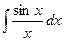; интегральный косинус 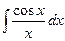; интегралы Френеля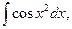 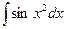.Указанные интегралы существуют, но наших средств недостаточно, чтобы составить из них конечные выражения для этих интегралов.