Задачи, приводящие к понятию определенного интеграла.

1. Задача о площади

В элементарной математике мы рассматривали площади прямолинейных фигур: прямоугольника, треугольника, трапеции и т.п. Рассмотрим фигуру ABCD , ограниченную кривой y=f(x), прямыми х=а и х= b, отрезком [а, b] оси ОХ. Будем называть такую фигуру криволинейной трапецией с основанием [а, b]. Разобьем отрезок [а, b] на n частей точками а = x_о, x₁, x₂,...., х_п= b, ( x_o< x₁< x₂<...< x_n).

Через точки деления проведем вертикальные прямые. При этом криволинейная трапеция ABCD разобьется на n криволинейных трапеций с основаниями [x_о, x₁,],[x₁, x₂],[x₂, xз],..., [х _n-1,х _n].

Внутри каждого из них выбираем произвольную точку ζ _i, x _i-1 < ζ _i < x_i, для которых вычисляем значения функции f(ζ_i). Площадь построенного прямоугольника с основанием [ x_n-1, x_n ] и h = f(ζ_i) будет равна произведению f(ζ_i) ( x_n-1, x_n)  

Рассмотрим ступенчатую фигуру, составленную из прямоугольников с основаниями [x_о, x₁,],[x₁, x₂],[x₂, xз],..., [х _n-1,х _n]. Ee площадь, равную сумме f(ζ₁) ( x_1, x₂)+ f(ζ₂) ( x_2, x₃)+ … + f(ζ_i) ( x_n-1, x_n),

будем считать приближенно равной площади криволинейной трапеции.

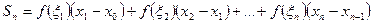
или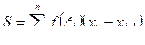      

Чем мельче отрезки деления, тем точнее эта ступенчатая фигура «изображает» криволинейную трапецию ABCD.

Если обозначить через 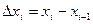, то за площадь необходимо

принять предел, к которому стремятся площади, построенных указанным образом ступенчатых фигур при неограниченном увеличении числа отрезков деления и стремления к нулю длин отрезков деления: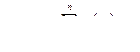

2. Задача о работе переменной силы    .

Материальная точка перемещается под действием силы , направленной вдоль оси ОХ и имеющей переменную величину 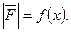 Требуется определить работу А, совершаемую силой  по перемещению единицы массы вдоль оси ОХ из точки х = а в точку x = b.

Если величина силы  неизменна, то работа (по определению) равна произведению величины силы на длину пути перемещения. В случае силы переменной величины работу можно определить аналогично предыдущему случаю: разбиваем отрезок [а, b] точками  на п отрезков [х₀, x₁ ], [x₁, х₂ ], ..., [х _n-1, х _n ],и на каждом отрезке [х _n-1, х _n ] выберем произвольную точку . Сила, действующая на отрезке [х _n-1, х _n ] меняется от точки к точке. Но если длина отрезка мала, ее величина в точке отрезка [х _n-1, х _n ] мало отличается от значения в точке , так как f(x) непрерывная функция.

Поэтому работу А_i, совершаемую силой  на отрезке [х _n-1, х _n], считаем приближенно равной работе, совершаемой на том же участке постоянной силой величины f( ), т. е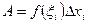

Проведя такие рассуждения, для каждого отрезка деления, имеем:

,

Точное значение работы А получаем в пределе при неограниченном увеличении числа отрезков деления и стремлении к нулю длин отрезков деления, т. е.

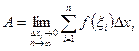
Таким образом, и в первой, и во второй задачах мы получили так называемые интегральные суммы , не зависящие ни

от способа разбиения отрезка [а, b] на части [х₀, x₁ ], [x₁, х₂ ], ..., [х _n-1, х _n ], ни от выбора точек 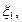 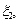…,  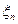 на этих частях. Таким образом, для функции f(x) на отрезке [а, b] можно составить бесчисленное множество интегральных сумм.

При неограниченном увеличении числа n отрезков и стремлении к нулю длин отрезов деления, будут изменяться и интегральные суммы. Назовем шагом разбиения отрезка [а, b] на части наибольшую из длин отрезков деления.

Будем говорить, что интегральная сумма функции f(x) при стремлении к нулю шага разбиения отрезка [а, b], имеют пределом число I, если для любого положительного числа ε > 0 существует положительное число δ > 0 такое, что все интегральные суммы с шагом разбиения меньшие δ, удовлетворяют неравенству

Число I, если оно существует, зависит только от вида f(x) и отрезка [а, b], но не зависит от способа разбиения отрезка [а, b] на части и выбора точек ζ_i, на этих частях. Это число I называется определенным интегралом от функции f(x) на отрезке [а, b].

Таким образом, определенный интеграл от функции f(x) на отрезке [а, b] есть' число, равное пределу интегральных сумм при стремлении к нулю шага разбиения отрезка [а, b]

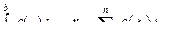
где λ – шаг разбиения отрезка [а, b];

a, b – нижний и верхний пределы интегрирования.

Теорема существования определенного интеграла.

Если функция f(x) непрерывна на конечном отрезке [а, b], то определенный интеграл существует.

Геометрический смысл определенного интеграла.

Он численно равен площади криволинейной трапеции с основанием [а, b] и ограниченной кривой f(x).