При определении интеграла 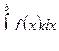 предполагалось, что нижний предел интегрирования меньше верхнего предела а < b.
предполагалось, что нижний предел интегрирования меньше верхнего предела а < b.
В случае если а > b, то 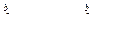 ,
,
если а = b, то 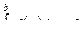 .
.
Свойства определенного интеграла.
1. Значение 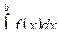 не зависит от обозначения переменной
не зависит от обозначения переменной
интегрирования, т. е 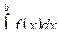 =
= 
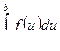 .
.
Это утверждение следует из определения определенного интеграла как числа, равного пределу интегральных сумм.
2. Определенный интеграл меняет знак при перестановке пределов интегрирования, т. е. при а > b.
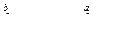
3. Постоянный множитель можно выносить за знак интеграла:
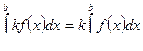 , где k - произвольная константа.
, где k - произвольная константа.
4. Определенный интеграл от суммы двух функций f1(x) и f2(x) равен сумме определенных интегралов от слагаемых, т. е.
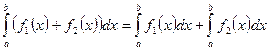 .
.
Примечание. Свойство 4 имеет место для любого числа слагаемых
5. Если отрезок [а, b] разбит точкой С на две части [а, c] и [c, b], то
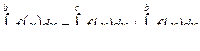 .
.
6. Для любого расположения точек а, b, с
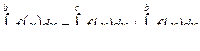
Пусть а< b < c, тогда применяя к [а, с] свойство 5:
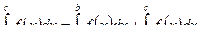
Но по свойству 2: 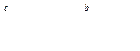 . Подставляя, полученные результаты получим:
. Подставляя, полученные результаты получим: 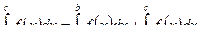 .
.
Аналогично доказывается для любого другого расположения а, b, с
Интегрирование неравенств.
7. Если всюду на отрезке [а, b]  , то
, то 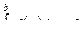
Доказательство:
Любая интегральная сумма  для f( x), на отрезке [а, b]
для f( x), на отрезке [а, b]
неотрицательна, т. к. 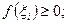
 i = 1, 2, …, n.
i = 1, 2, …, n.
Переходя к пределу в неравенстве 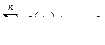 , получаем
, получаем
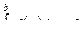 .
.
8. Если всюду на отрезке [а, b]  , то
, то 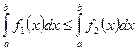
Доказательство:
T. к. на [а, b] 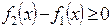 ,
,
то по свойству 7:
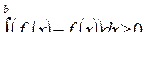
по свойству 5:
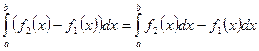
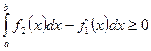 , т.е.
, т.е. 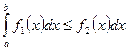 .
.
9. Если функция f( x) непрерывна на отрезке [а, b],
неотрицательна и неравна 0, то 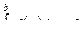 .
.
Доказательство:
По условию найдена такая точка x0 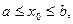 что f( x)>0.
что f( x)>0.
В силу непрерывности функции f( x) на 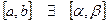 ,
,
содержащий точку x0, на которой  .
.
Используя свойства 6, 7, 8, 4, 3, получаем, что
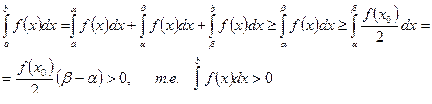
10. Для функции f( x), заданной на отрезке [а, b], имеет место

(модуль определенного интеграла от некоторой функции не превосходит интеграла от модуля этой функции)
Доказательство:
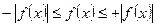
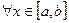 ,
,
отсюда следует, что 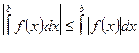 .
.
11. Грубая оценка определенного интеграла.
Пусть дана функция f( x), причем, m и M –наименьшее и наибольшее значение функции f( x) на отрезке [а, b], т. е.
Объем тела вращения
 Рассмотрим на плоскости XOY кривую y = f( x), непрерывную на отрезке [а, b]. Если соответствующую ей криволинейную трапецию с основанием [а, b] вращать вокруг оси ОХ, то образуется так называемое тело вращения. Произвольное сечение тела плоскостью x = const,
Рассмотрим на плоскости XOY кривую y = f( x), непрерывную на отрезке [а, b]. Если соответствующую ей криволинейную трапецию с основанием [а, b] вращать вокруг оси ОХ, то образуется так называемое тело вращения. Произвольное сечение тела плоскостью x = const,
перпендикулярной оси ОХ, есть круг, площадь которого
 где радиус круга
где радиус круга 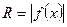
Получаем формулу для вычисления объема тела
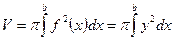
Замечание. Если необходимо найти объем тела, получаемого вращением кривой 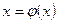 вокруг оси OY, то
вокруг оси OY, то
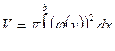
Пример 62.
Найти объем тела, ограниченного поверхностью полученной вращением функции у = х3 на отрезке [0,1] вокруг оси ОХ
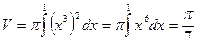
Площадь поверхности тела вращения
Пусть дана поверхность, образованная вращением функции y = f( x) вокруг оси ОХ. Функция f( x) непрерывна и имеет производные во всех точках
Тогда  .
.
Следовательно, длина дуги кривой в полярной системе координат
 ( 3 )
( 3 )
Вычисление объема тела по известным поперечным сечениям

Предположим, что известна площадь произвольного сечения тела плоскостью, перпендикулярной оси ОХ.
Эта площадь будет зависеть от положения секущей плоскости, т. е.
S = S( x).
Проведем плоскости
х = х0 = а, х = x1, х = х2, ..., х = x i, ..., х = хп = b.
И плоскости разобьют тело на слои. В каждом частичном отрезке 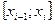 выберем произвольную точку
выберем произвольную точку  и для каждого i =1, 2, .., n построим цилиндрическое тело. Объемы таких маленьких цилиндров с площадью основания S(
и для каждого i =1, 2, .., n построим цилиндрическое тело. Объемы таких маленьких цилиндров с площадью основания S(  ) и высотой ∆ xi:
) и высотой ∆ xi:
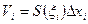
Объем всех цилиндров
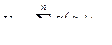
Предел этой суммы, если он существует, называется объемом тела

по свойству 5:
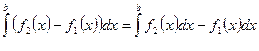
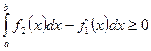 , т.е.
, т.е. 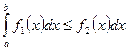 .
.
9. Если функция f( x) непрерывна на отрезке [а, b],
неотрицательна и неравна 0, то 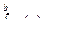 .
.
Доказательство:
По условию найдена такая точка x0 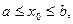 что f( x)>0.
что f( x)>0.
В силу непрерывности функции f( x) на 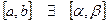 ,
,
содержащий точку x0, на которой 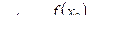 .
.
Используя свойства 6, 7, 8, 4, 3, получаем, что
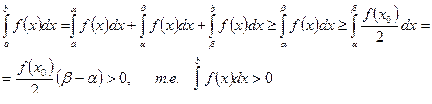
10. Для функции f( x), заданной на отрезке [а, b], имеет место
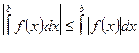
(модуль определенного интеграла от некоторой функции не превосходит интеграла от модуля этой функции)
Доказательство:
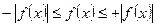
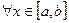 ,
,
отсюда следует, что  .
.
11. Грубая оценка определенного интеграла.
Пусть дана функция f( x), причем, m и M –наименьшее и наибольшее значение функции f( x) на отрезке [а, b], т. е.
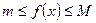 . Применяя к этому неравенству свойство 8, имеем
. Применяя к этому неравенству свойство 8, имеем
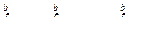 .
.
Интеграл слева равен площади прямоугольника с основанием
( b - а) и высотой m и он равен 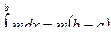 .
.
Интеграл справа равен площади прямоугольника с тем же основанием ( b - а) и высотой М 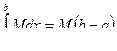 .
.
Таким образом, получаем выражение для грубой оценки определенною интеграла: 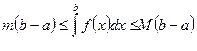 .
.
Геометрический смысл этой оценки очень прост:
площадь криволинейной трапеции не больше плошали описанного,
но не меньше площади вписанного прямоугольников
12. Теорема о среднем значении f( x), на отрезке [а,b ]:
существует точка 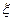 , принадлежащая отрезку, где функция f( x), принимает среднеарифметическое значение:
, принадлежащая отрезку, где функция f( x), принимает среднеарифметическое значение: 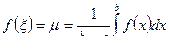
Действительно: на основании грубой оценки определенного
интеграла и, разделив все члены выражения на ( b - а), имеем 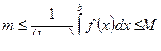 откуда
откуда  . Вследствие непрерывности, функция f( x) принимает хотя бы один раз все значения между m и М, а, следовательно, и значение μ. Поэтому существует точка
. Вследствие непрерывности, функция f( x) принимает хотя бы один раз все значения между m и М, а, следовательно, и значение μ. Поэтому существует точка 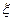
 [а, b],
[а, b],
где f( 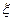 ) = μ, т е.
) = μ, т е. 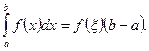
13. Производная от интеграла по его верхнему пределу.
Пусть f( x) – функция, непрерывная на отрезке [а, b], а значит она интегрируема на любом отрезке [а, x], где  . Пусть в определенном интеграле нижний a предел закреплен, а верхний b - меняется. Тогда будет меняться и значение интеграла т. е. интеграл есть функция верхнего предела:
. Пусть в определенном интеграле нижний a предел закреплен, а верхний b - меняется. Тогда будет меняться и значение интеграла т. е. интеграл есть функция верхнего предела: 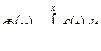
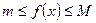 . Применяя к этому неравенству свойство 8, имеем
. Применяя к этому неравенству свойство 8, имеем
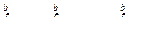 .
.
Интеграл слева равен площади прямоугольника с основанием
( b - а) и высотой m и он равен 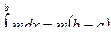 .
.
Интеграл справа равен площади прямоугольника с тем же основанием (b - а) и высотой М 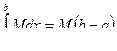 .
.
Таким образом, получаем выражение для грубой оценки определенного интеграла: 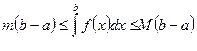 .
.
Геометрический смысл этой оценки очень прост:
площадь криволинейной трапеции не больше площади описанного,
но не меньше площади вписанного прямоугольников
12. Теорема о среднем значении f( x), на отрезке [а,b]:
существует точка 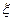 , принадлежащая отрезку, где функция f( x) принимает среднеарифметическое значение:
, принадлежащая отрезку, где функция f( x) принимает среднеарифметическое значение: 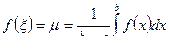 .
.
Действительно: на основании грубой оценки определенного интеграла и, разделив все члены выражения на (b – а), имеем,
 откуда
откуда 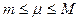 . Вследствие непрерывности, функция f( x) принимает хотя бы один раз все значения между m и М, а, следовательно, и значение μ. Поэтому существует точка
. Вследствие непрерывности, функция f( x) принимает хотя бы один раз все значения между m и М, а, следовательно, и значение μ. Поэтому существует точка 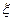
 [а, b],
[а, b],
где f( 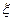 ) = μ, т е.
) = μ, т е. 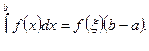
13. Производная от интеграла по его верхнему пределу.
Пусть f( x) – функция, непрерывная на отрезке [а, b], а значит, она интегрируема на любом отрезке [а, x], где  . Пусть в определенном интеграле нижний a предел закреплен, а верхний b – меняется. Тогда будет меняться и значение интеграла, т. е. интеграл есть функция верхнего предела:
. Пусть в определенном интеграле нижний a предел закреплен, а верхний b – меняется. Тогда будет меняться и значение интеграла, т. е. интеграл есть функция верхнего предела: 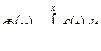 .
.
Теорема Барроу.
 Если функция f( x) – непрерывная функция и
Если функция f( x) – непрерывная функция и 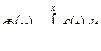 , то имеет место равенство
, то имеет место равенство 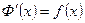 ;
;
иными словами:
производная от определенного
интеграла по верхнему пределу
равна подынтегральной функции,
в которую вместо переменной
интегрирования подставлено
значение верхнего предела.
Доказательство:
Дадим переменной x приращение ∆ x (∆x > 0 или ∆ x < 0) тогда, учитывая свойство 5, имеем:
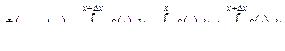
Приращение функции 
то есть 
Применяя к этому интегралу теорему о среднем
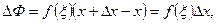 где
где 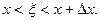
Найдем отношение приращения функции к приращению аргумента

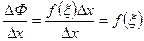 .
.
Следовательно, 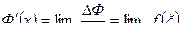
Но так как  при
при 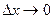 ,
,
то  (вследствие непрерывности функции f( x)).
(вследствие непрерывности функции f( x)).
Таким образом, Ф'(х) = f( x))
Формула Ньютона-Лейбница.
Теорема. Если F(x) - какая-либо первообразная от непрерывной функции f( x), то справедлива формула 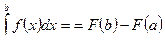
1 Доказательство:
Пусть F(x) – некоторая первообразная от функции f( x),. По теореме
Барроу функция 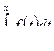 – также первообразная от функции f( x). Но две произвольные первообразные отличаются от функции на постоянную величину, т. е.
– также первообразная от функции f( x). Но две произвольные первообразные отличаются от функции на постоянную величину, т. е. 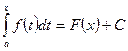 .
.
Для определения С положим х =а, тогда  ,
,
0 = F(a) + C, C = – F(a)
Следовательно,  . Полагая x=b, получим
. Полагая x=b, получим  или, заменив обозначение переменной интегрирования на x (т. к. от переобозначения переменной интегрирования значение интеграла не зависит), получим формулу Ньютона-Лейбница:
или, заменив обозначение переменной интегрирования на x (т. к. от переобозначения переменной интегрирования значение интеграла не зависит), получим формулу Ньютона-Лейбница: 
Эта формула показывает, что определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленной для верхнего и нижнего пределов интегрирования..
Пример 49.
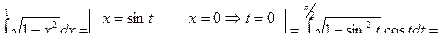

Дата: 2018-12-28, просмотров: 398.