Пусть в некоторой (открытой) области задана функция двух перемен­ных z=f(x, y). Возьмем произвольную М(х, у) этой области и дадим х при­ращение Δх, оставляя значение у неиз­менным. При этом функция f(x, y) полу­чит приращение Δ_xz=f(x+Δx,y)-f(x,y). Оно называется частным при­ращением этой функции по х (рис 15)

дает среднюю скорость измене­ния функ­ции z=f(x, y) по пере­менной х на участке от точки М(х,у) до точки М'(х+Δх,у).      

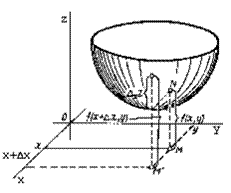
 Рисунок 16

Пре­дел этого отношения при Δх→0, если он существует и конечен, назы­вается частной производной функции z=f(x,y) по переменной х в точке (х,у). Этот предел характеризует скорость изменения данной функции по х в самой точке М. Частную производную по х от функции z=f(x,y) обознача-

ют следующими символами:

       Таким образом,

Аналогично, считая х постоянной и давая у приращение Δу, мы полу­чим  частное приращение  функции z = f(х, у) по у:

              Δ_yz= f( x, y + Δy ) – f( x, y)      (рис. 17)

Предел отношения частного приращения функции по у к прираще­нию Δу при стремлении последнего к нулю (если он существует и коне­чен) на­зывается частной производной этой функции по у в точке (х, у).

Частная производная функции z=f(х, у) по у обозначается обычно од­ним из следующих символов:

 Таким образом,       

Значения частных производных f'_х(х,у) и f'_у(х,у),естественно, зави­сят от координат х, у рас­смат­риваемой точки М, т.е. ча­стные производные f'_х(х,у) и f'_у(х,у), в свою очередь, являются функциями двух переменных, определенными в заданной об­ласти или ее части (если не во   

 всех точках этой области суще­ст­ вуют частные производные).

                              Рисунок 17

Вычисление частных производных по х (по у) от конкретных функций производится по известным для функций одной переменной пра­вилам, так как частная производная функция z = f(х, у)  по  х (по у) есть по опреде­лению обыкновенная производная функции z = f(х, у), рассматривае­мой как функция одной перемен­ной х (соответственно у) при по­стоянном зна­чении другой пере­менной.

Например, для функции

 f(х, у) = х² + ху² + у³ в любой точке (х, у) имеем f'х(х, у)= 2х+ у², f'_у(х,у) = 2ху + 3у². В частности, f'_х(1,2) = 2∙1+2²= 6, f'_у(1,2) = 2∙ 1∙ 2+ +3∙2² = 16.

                                                                         Рисунок 18

   Частные производные функции двух переменных имеют простой

геометрический смысл.

   Рассмотрим в пространстве XYZ поверхность S, имеющую уравнение

z= f(х, у). Эта поверхность изображает функцию f(х, у).

       Дадим переменным х  и у  значения  х₀, у₀. По определению f'_х(х₀, у₀) есть обыкновенная производная (по х) от функции одной переменной 

f(х, у₀)  при х = х₀. График этой функции мы получим в сечении поверх­ности S плоскостью у = у₀.

Так как производная функции одной переменной  х в данной точке равна тангенсу угла наклона к оси ОХ касательной к графику функции в этой точке, заключаем, что f'_х(х₀, у₀) есть тангенс угла φ, составленного с осью ОХ касательной, проведенной в точке N₀ (х₀, у₀, f(х₀, у₀)) к сече­нию поверхности S плоскостью у = у₀ ( рис. 18).

Аналогично f'_у(х₀, у₀) есть тангенс угла θ, составляемого с осью OY касательной, проведенной в точке N₀ к сечению поверхности S плоско­стью х = х₀  (рис. 19).

Для функций любого числа п  переменных частные производные вво­дятся так же, как и для функций двух переменных. А именно, частная производная от функций и = f ( х, у, z,…w ) по любому из независимых переменных в точке ( х, у, z,…w) есть предел отношения частного прира­щения функции в этой точке к приращению соответствующей независи­мой переменной при стремлении последнего к нулю ( если этот предел существует и конечен). Обозначения аналогичны при­веденным выше.

    Например, если и=f(х, у,z),

то