Вводя определенный интеграл как предел интегральных сумм, мы предполагали, что отрезок интегрирования конечный, а подынтегральная функция непрерывна и ограничена на данном отрезке. Если хотя бы одно из этих условий не выполнено, данное выше определение теряет смысл.
Интегралы с бесконечными пределами интегрирования
Пусть f(x) определена и непрерывна для любых x, таких, что . 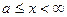 Рассмотрим
Рассмотрим 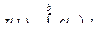
Этот интеграл имеет смысл для любых b> а . При изменении b I(b) изменяется, и на основании теоремы Барроу он является непрерывной функцией Пусть b→∞.
Определение. Если существует конечный предел 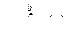 , то этот предел называется несобственным интегралом 1 рода от функции f(х) на [а,∞);
, то этот предел называется несобственным интегралом 1 рода от функции f(х) на [а,∞);
Обозначают  , т. е.
, т. е.  =
= 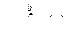
говорят, что в этом случая несобственный интеграл  существует или сходится.
существует или сходится.
Если интеграл  при b→∞.не имеет предела, то говорят, что
при b→∞.не имеет предела, то говорят, что  не существует или расходится.
не существует или расходится.
Аналогично определяются несобственные интегралы для других бесконечных интервалов
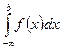 =
= 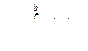
Для функции f ( x), непрерывной на всей числовой оси:
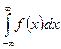 =
= 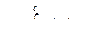 +
+ 
Последнее равенство понимается так: если каждый из несобственных интегралов, стоящих справа, существует, то существует (сходится), по определению интеграл, стоящий слева. Если хотя бы один из интегралов, стоящих справа расходится, то расходится и интеграл, стоящий слева.
Пример 51. 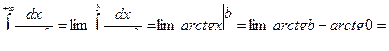
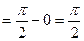
Определенные выше интегралы обладают рядом свойств, присущих обыкновенным определенным интегралам.  Для них можно получить формулу Ньютона-Лейбница.
Для них можно получить формулу Ньютона-Лейбница.
Пусть функция f(х) непрерывна на промежутке [a;∞] и имеет на
нем первообразную F' (х). Тогда для любого b, а< b по формуле Ньютона- Лейбница имеем:

Отсюда следует, что несобственный интеграл  существует в том, и только в том случае, когда существует предел F(b) при b→∞. Если этот предел существует, то
существует в том, и только в том случае, когда существует предел F(b) при b→∞. Если этот предел существует, то 
Пусть 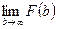 )= F(+∞), тогда
)= F(+∞), тогда 
Последняя формула носит название обобщенной формулы Ньютона-Лейбница для случая несобственного интеграла. Аналогично

 ,
,
где под F(-∞) понимают 

Пример 52
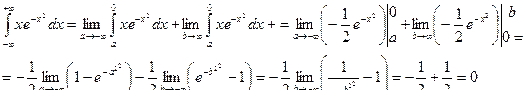
 - сходится.
- сходится.
Во многих задачах, связанных с несобственными интегралами, достаточно только выяснить вопрос о сходимости рассматриваемого интеграла и не требуется находить его значение.
Необходимое условие сходимости несобственного интеграла.
Если  сходится, то его частные интегралы ограничены, т. е. существует такое М > 0, что для всех b > а
сходится, то его частные интегралы ограничены, т. е. существует такое М > 0, что для всех b > а 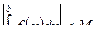
Это утверждение вытекает из существования конечного предела частных интегралов при b → ∞
Таким образом, если частные интегралы не ограничены, то несобственный интеграл расходится. Если же частные интегралы ограничены, то о сходимости интеграла еще ничего сказать нельзя: в одних случаях он может сходиться, а в других - расходиться.
Пример 53.
 . Частный интеграл
. Частный интеграл  - ограничен, но он не имеет предела при b → ∞, т. к. sin Ь не имеет предела при b → ∞,, и, следовательно,
- ограничен, но он не имеет предела при b → ∞, т. к. sin Ь не имеет предела при b → ∞,, и, следовательно,  расходится. Аналогично расходится интеграл
расходится. Аналогично расходится интеграл 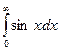
Принцип сравнения несобственных интегралов
Если функции f{x) и φ( x) непрерывны на [a;+∞] и удовлетворяют на нем условию 0 ≤ f{x) ≤ φ( x), то из сходимости интеграла 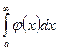 следует сходимость
следует сходимость 
Следствие. Если функции f(х) и φ( x) на [a;∞] и  ,
,
где h – постоянная величина, то интегралы  и
и 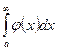
ведут себя одинаково относительно сходимости.
Пример 54.
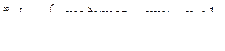
т.к. 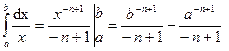
если учесть, что 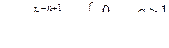 ,
,  сходится при n>1 и расходится при n<1
сходится при n>1 и расходится при n<1
если n = 1, то 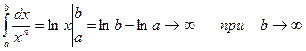 , т. е. расходится.
, т. е. расходится.
Пример 55.

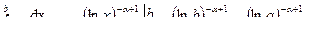
Т.к. 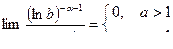 ,
, 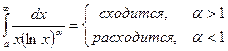 ,
,
если a = 1, то 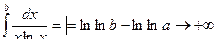 , т. е. интеграл расходится.
, т. е. интеграл расходится.
Пусть функция f(х) непрерывна на [а,+∞] и необязательно знакопостоянна. Интеграл  называется абсолютно сходящимся, если сходится интеграл.
называется абсолютно сходящимся, если сходится интеграл. 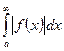 Тогда признак сходимости неопределенного интеграла для знакопеременной функции f(х) может быть сформулирован следующим образом: если сходится,
Тогда признак сходимости неопределенного интеграла для знакопеременной функции f(х) может быть сформулирован следующим образом: если сходится, 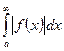 , то сходится интеграл
, то сходится интеграл 
Пример 56.
Определить сходимость интеграла 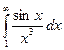
 но
но  , значит,
, значит,  сходится, тогда
сходится, тогда
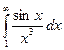 – сходится
– сходится
Интеграл от разрывной функции
Интегралы от разрывных функций иначе называют интегралами 2 рода. Пусть функция f(х) непрерывна при x < с, а при x = с функция f(х) либо неопределенна, либо терпит разрыв. В этом случае нельзя говорить об интеграле как о пределе интегральных сумм, так как f(х) не непрерывна на [а, с] и поэтому этот интеграл не может существовать.
Несобственные интегралы второго рода имеют место в том случае, если функция f(х) терпит разрыв второго рода.
Несобственным интегралом второго рода от функции f(х) непрерывной на [а,с] и терпящей разрыв при x = с, называется

Если указанный предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.
Аналогично определяется интеграл с разрывом функции в начале интервала 
Пример 57.

Пример 58.
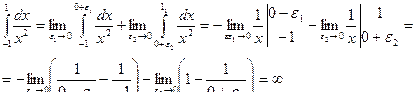
На [-1,0] интеграл расходится и на [0,1] он также расходится, значит и на всем [-1,1] интеграл расходится.
А если бы мы не обратили внимание на разрыв в точке x = 0, то
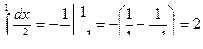 , что неверно.
, что неверно.
Замечание. Если функция f{x) определена на [а, b] и имеет внутри [[а, b]] конечное число точек разрыва а1, а2,-.. an, то
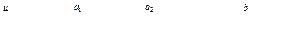
сходится, если каждый из несобственных интегралов в правой части сходится. Если хотя бы один из этих интегралов расходится, то интеграл  называется расходящимся.
называется расходящимся.
Все утверждения и теоремы, рассмотренные для несобственных интегралов 1 рода (интегралы с бесконечными пределами интегрирования) справедливы и для несобственных интегралов 2 рода
Теорема 1. Если на отрезке [а, с] функции f( x) и φ( x) терпят разрыв в точке x = с, причем во всех точках этого отрезка φ( x)≥ f( x)≥0, то из сходимости  следует сходимость интеграла
следует сходимость интеграла 
Теорема 2. Если функция знакопеременная на отрезке [а, с] и в точке x = с терпит разрыв и, кроме того, интеграл  сходится, то интеграл
сходится, то интеграл  также будет сходиться.
также будет сходиться.
Замечание к теореме 1. В качестве функций φ( x), с которыми удобно сравнивать функции, стоящие под знаком интеграла, берут функцию  для которой
для которой
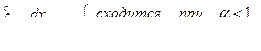
Это относится к интегралу 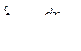 .
.
Пример 58.
Исследовать на сходимость 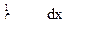 .
.
На левом конце отрезка [0,1] подынтегральная функция терпит разрыв. 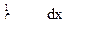 сходится, т. к.
сходится, т. к. 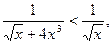
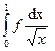 существует, тогда
существует, тогда 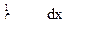 также существует.
также существует.
Пример 59.
Исследовать на сходимость 
Геометрические приложения определенного интеграла
При решении задач о вычислении площади криволинейной трапеции, ограниченной снизу отрезком [a, b] оси ОХ, сверху - кривой у = f(х) (f(х) – непрерывна, неотрицательна), слева прямой x = а , справа прямой х = b, мы получим:
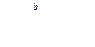
Если f (x) непрерывна и не положительна на [a,b], то 
Абсолютная величина этого интеграла
равна площади криволинейной трапеции, ограниченной сверху отрезком [a,b] оси
ОХ, слева прямой x = а , справа – прямой
х = b, снизу - кривой у = f(х); в этом
случае площадь криволинейной трапеции

Если у = f(x) непрерывна на отрезке [а,Ь] и не знакопостоянна, то определенный интеграл численно равен алгебраической сумме площадей криволинейных трапеций, лежащих над и под осью ОХ.
В эту сумму площади криволинейных трапеций, лежащих над осью ОХ, входят со знаком «+», а площади криволинейных трапеций, лежащих под осью ОХ – со знаком «–»
Рассмотрим фигуру ABCD, ограниченную слева и справа прямыми x = а и х = b, снизу и сверху – кривыми у = f1(х) и у = f2(х), где f1(х) и f2(х) – непрерывные функции на [a,b].


Если обе функции f1(x), f2(x) на отрезке [а, b] неотрицательны или неположительные, то площадь SABCD можно вычислить как разность площадей криволинейных трапеций LKCD и LKBA (а, в), т. е
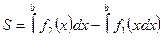
или
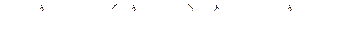
Если функция f1(x), не положительна f1(x)≤ 0,, а функция f2(x) неотрицательна f2(x) ≥ 0 на отрезке [а, b] , то площадь SABCD будет равна сумме площадей S LKCD и SLKBA (в), т. е.


Таким образом, площадь фигуры ABCD во всех случаях может быть вычислена по формуле
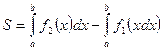
Пример 60.
Вычислить площадь, ограниченную кривой у = sin x с осью ОХ при 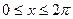
Так как 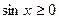 при
при  и
и 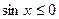 при
при 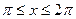 , то
, то
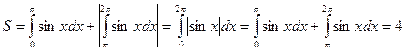
Если кривая задана параметрически, то площадь криволинейной трапеции, ограниченной кривой, заданной параметрически, может быть вычислена из формулы:
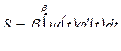 ,
,
где 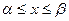 и
и  ,
, 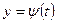 и
и  ,
, 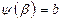
Пусть функция y = f( x) на отрезке [а, b] определяется уравнением:

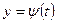
Площадь фигуры, ограниченная данной кривой:

Сделаем замену:
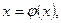
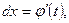
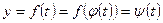
И, следовательно

Пример 61
Вычислить площадь фигуры, ограниченную осью ОХ и одной циклоиды
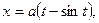
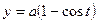
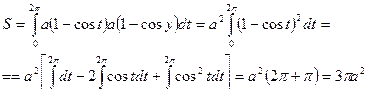
 Криволинейным сектором называется фигура, ограниченная дутой
Криволинейным сектором называется фигура, ограниченная дутой 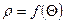 , начальным и конечным радиусами этой дуги.
, начальным и конечным радиусами этой дуги.
Площадь криволинейного сектора
Пусть имеем полярную систему координат  . Рассмотрим криволинейный сектор ОАВО, ограниченный лучом ОА и ОВ, составляющей с полярной осью
. Рассмотрим криволинейный сектор ОАВО, ограниченный лучом ОА и ОВ, составляющей с полярной осью 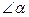 и
и  где
где 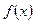 – непрерывная неотрицательная
– непрерывная неотрицательная
функция 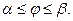
Разобьем 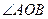 лучами φ = φ0 = a, φ = φ1, …, φ = φ n = b
лучами φ = φ0 = a, φ = φ1, …, φ = φ n = b
на n частей.
Обозначим точки пересечения этих лучей с кривой 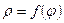 через A0, A1, ..., A n. Криволинейный сектор разобьется на n криволинейных секторов.
через A0, A1, ..., A n. Криволинейный сектор разобьется на n криволинейных секторов.

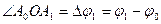
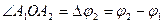
…………………………
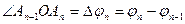
Для каждого сектора определить наибольшее - R i и наименьшее r i значения 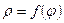 на
на 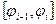
Построим круговые секторы радиусов R i, и r i с тем же углом при вершине
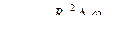

Фигуру Q, составленную из всех круговых секторов радиусов R i, (i = l, .., n), называют описанной вокруг данного криволинейного сектора. Она содержит данный сектор. Фигура q, составленная из круговых секторов r i, называется вписанной – она содержится в данном криволинейном секторе.
При этом
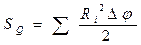
Т. к. полученные суммы представляют собой интегральные суммы
(верхнюю и нижнюю) для непрерывной на 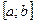 функции
функции  , то при стремлении к нулю наибольшего из углов деления, эти
, то при стремлении к нулю наибольшего из углов деления, эти  общего предела.
общего предела.
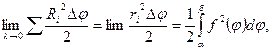
 Отсюда следует, что любая последовательность разбиений
Отсюда следует, что любая последовательность разбиений 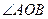 на части с шагом разбиения λ → 0, площади соответствующих описанных и вписанных фигур имеющих общий предел, равный
на части с шагом разбиения λ → 0, площади соответствующих описанных и вписанных фигур имеющих общий предел, равный 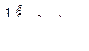 . т. е.
. т. е.
площадь криволинейного сектора
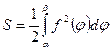
или

Пример.
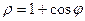
Кардиоида
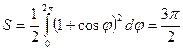
Длина дуги кривой.
Длиной дуги L называется предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена λ стремится к нулю:
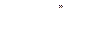
1. Длина дуги кривой в декартовых координатах.
Найдем длину дуги АВ кривой у = f( x), заключенной между прямыми x = а и х = b
Пусть на отрезке [а, b] функция у = f( x) непрерывна вместе со своей производной у = f'( x).
Пусть 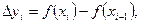 тогда
тогда
 .
.
Используя теорему Лагранжа о конечных приращениях, получим:


где  .
.
Следовательно,
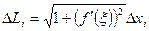
Таким образом, длина вписанной ломаной равна
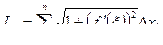 .
.
По условию f'(x) непрерывна, тогда 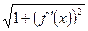 тоже непрерывна. Поэтому существует предел интегральной суммы, который равен определенному интегралу:
тоже непрерывна. Поэтому существует предел интегральной суммы, который равен определенному интегралу:
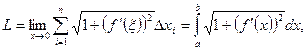
т. е. длина дуги кривой, заданной явно: у = f( x):
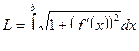
2. Длина дуги кривой в параметрической Форме.
Пусть кривая у = f( x) задана в параметрической форме
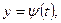
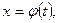
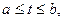
где функции φ( t)и ψ( t) непрерывны вместе со своими производными φ'( t)и ψ'( t).
Производная функции, заданной параметрически:
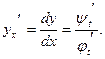
Пусть 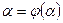 ,
, 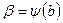 . Сделаем подставку
. Сделаем подставку 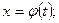
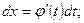 . Подставляя полученные результаты в формулу определения длины дуги АВ кривой y = f( x)
. Подставляя полученные результаты в формулу определения длины дуги АВ кривой y = f( x)
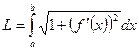 ,
,
получаем

Таким образом, если кривая задана параметрически, то длина дуги данной кривой
 ( 2 )
( 2 )
3. Длина дуги кривой в полярных координатах.
Пусть в полярной системе координат уравнение кривой задано в виде 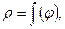 где ρ - полярный радиус, φ- полярный угол.
где ρ - полярный радиус, φ- полярный угол.
Формулы перехода от полярных координат к декартовым:

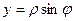
Если вместо ρ подставим его выражение 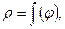 , то получим:
, то получим:
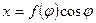
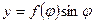
Эти уравнения можно рассматривать как параметрические и применить к ним формулу (2), где 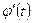 будет представлять:
будет представлять:

 .
.
Тогда  .
.
Следовательно, длина дуги кривой в полярной системе координат
 ( 3 )
( 3 )
Вычисление объема тела по известным поперечным сечениям

Предположим, что известна площадь произвольного сечения тела плоскостью, перпендикулярной оси ОХ.
Эта площадь будет зависеть от положения секущей плоскости, т. е.
S = S( x).
Проведем плоскости
х = х0 = а, х = x1, х = х2, ..., х = x i, ..., х = хп = b.
И плоскости разобьют тело на слои. В каждом частичном отрезке 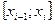 выберем произвольную точку
выберем произвольную точку  и для каждого i =1, 2, .., n построим цилиндрическое тело. Объемы таких маленьких цилиндров с площадью основания S(
и для каждого i =1, 2, .., n построим цилиндрическое тело. Объемы таких маленьких цилиндров с площадью основания S(  ) и высотой ∆ xi:
) и высотой ∆ xi:
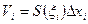
Объем всех цилиндров
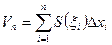
Предел этой суммы, если он существует, называется объемом тела
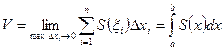
Объем тела вращения
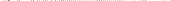 Рассмотрим на плоскости XOY кривую y = f( x), непрерывную на отрезке [а, b]. Если соответствующую ей криволинейную трапецию с основанием [а, b] вращать вокруг оси ОХ, то образуется так называемое тело вращения. Произвольное сечение тела плоскостью x = const,
Рассмотрим на плоскости XOY кривую y = f( x), непрерывную на отрезке [а, b]. Если соответствующую ей криволинейную трапецию с основанием [а, b] вращать вокруг оси ОХ, то образуется так называемое тело вращения. Произвольное сечение тела плоскостью x = const,
перпендикулярной оси ОХ, есть круг, площадь которого
 где радиус круга
где радиус круга 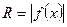
Получаем формулу для вычисления объема тела
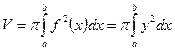
Замечание. Если необходимо найти объем тела, получаемого вращением кривой 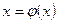 вокруг оси OY, то
вокруг оси OY, то
Пример 62.
Найти объем тела, ограниченного поверхностью полученной вращением функции у = х3 на отрезке [0,1] вокруг оси ОХ
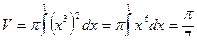
Площадь поверхности тела вращения
Пусть дана поверхность, образованная вращением функции y = f( x) вокруг оси ОХ. Функция f( x) непрерывна и имеет производные во всех точках
65
 Разобьем точками деления дугу АВ на части. Выделим бесконечно малый элемент дуги и заменим его отрезком касательной длиной
Разобьем точками деления дугу АВ на части. Выделим бесконечно малый элемент дуги и заменим его отрезком касательной длиной 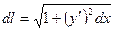 ,
,
вращая который вокруг оси ОХ получим усеченной конус, площадь поверхности которого

Интегрируя в пределах от a до b, получаем:
 .
.
Приложение определенного интеграла к механике
Пусть на плоскости XOY дана система материальных точек
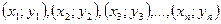 с массами m1, m2, m3, …, mn .
с массами m1, m2, m3, …, mn .
xi , mi ; yi , mi – статические моменты массы mi относительно осей ОХ и OY.
Координаты центра тяжести:
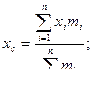
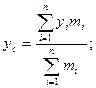
Центр тяжести плоской линии
Пусть кривая у = f(x) на отрезке [а, b] представляет собой материальную линию, а γ - линейную плотность (где линейная плотность - масса единицы длины данной линии). Разобьем линию на n частей длины ∆L1, ∆L2, ..., ∆Ln.
Массы этих частей будут равны произведению их длин на линейную плотность:
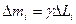
66
На каждой части дуги ∆ Li возьмем произвольную точку с абсциссой  . Представляя теперь каждую часть дуги ∆ Li точкой
. Представляя теперь каждую часть дуги ∆ Li точкой 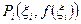 с массой
с массой 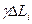 , и подставляя вместо
, и подставляя вместо 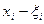 , а вместо
, а вместо 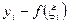 в формулы определения координат центра тяжести, получим:
в формулы определения координат центра тяжести, получим:
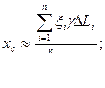
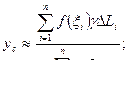
Если функция f(x) непрерывна и имеет непрерывную производную, то суммы каждого из произведений при стремлении к нулю наибольшей части дуги ∆ Li имеют предел, равный пределу соответствующих интегральных сумм.
Таким образом, координаты центра тяжести дуги:
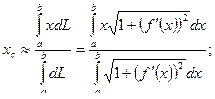
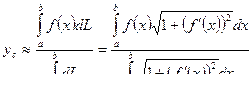 .
.
Центр тяжести плоской фигуры
Пусть на плоскости XOY дана фигура ABCD, ограниченная кривыми 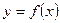 , и прямыми х = a , x = b, которая представляет собой материальную плоскую фигуру. Поверхностную плотность, т. е. массу единицы площади поверхности
, и прямыми х = a , x = b, которая представляет собой материальную плоскую фигуру. Поверхностную плотность, т. е. массу единицы площади поверхности
мы будем считать постоянной, равной 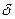 для всех частей фигуры. Разобьем данную фигуру прямыми x = х0 = a, x = x1, х = х2, ..., х = хт = b на плоскости шириной ∆х1„∆х2,..., ∆хn.
для всех частей фигуры. Разобьем данную фигуру прямыми x = х0 = a, x = x1, х = х2, ..., х = хт = b на плоскости шириной ∆х1„∆х2,..., ∆хn.
Масса каждой полоски будет равна произведению ее площади на поверхностную плотность 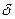 . Если каждую полоску заменить прямоугольником с основанием ∆х1 и высотой
. Если каждую полоску заменить прямоугольником с основанием ∆х1 и высотой 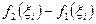 ,
,
где 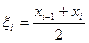 , тогда масса
, тогда масса  полоски приближенно будет равна:
полоски приближенно будет равна:
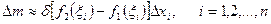
Центр тяжести такой полоски будет находится в центре соответствующего прямоугольника:
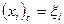 ;
; 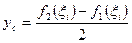
Заменяя теперь каждую полоску материальной точкой, масса которой равна массе соответствующей полоски и сосредоточена в центре тяжести этой полоски, найдем приближенное значение координат центра тяжести всей фигуры
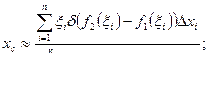
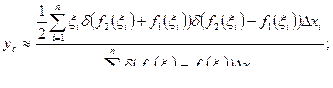
Переходя к пределу при ∆х i —> 0, получим точные значения координат центра тяжести фигуры:
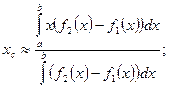
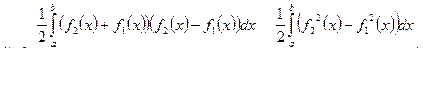
Эти формулы справедливы для любой однородной (имеющей постоянную плотность во всех точках) плоской фигуры.
Координаты центра тяжести не зависят от плотности 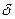 .
.
Теорема Паппа-Гульдина
Ордината центра тяжести дуги плоской кривой:
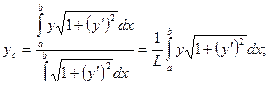
где 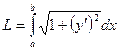 – длина дуги кривой.
– длина дуги кривой.
Преобразуем:
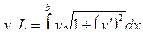 (1)
(1)
Площадь поверхности тела вращения
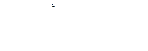
или
 (2)
(2)
Сравнивая уравнения (1) и (2), получаем (если правые части уравнений равны, то равны и левые части):
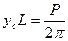 или
или  (3)
(3)
Полученное выражение (3) составляет содержание
1 Теоремы Паппа-Гульдина: Площадь поверхности тела вращения равна произведению длины окружности, описываемой центром тяжести кривой, на длину этой кривой.
Ордината центра тяжести плоской фигуры:
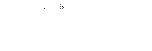 ,
,
где
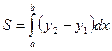 – площадь фигуры
– площадь фигуры
или
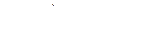 ( 4 )
( 4 )
Объем тела вращения:
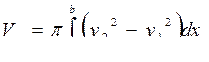
или
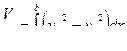 ( 5 )
( 5 )
Сравнивая уравнения (4) и (5) получаем:
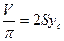
или
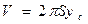 ( 6 )
( 6 )
Полученное выражение (6) составляет содержание
2 Теоремы Паппа-Гульдина: Объем тела вращения равен произведению длины окружности, описываемой центром тяжести фигуры на ее площадь.
Механическое приложение определенного интеграла.
Вычисление силы давления жидкости.
Пусть имеется резервуар, имеющий форму прямоугольного параллелепипеда, с размерами оснований а, b и высотой h, наполненный водой. Найдем общую силу Р давления воды на стенки резервуара.
Физические приложения определенного интеграла
В задачах, приводящих к понятию определенного интеграла, мы рассматривали работу по перемещению точки из a в b под действием переменной силы F. Сила направлена по оси ОХ и зависит только от x.
Сила давления жидкости Р плотности ρ на вертикальную пластинку, погруженную в жидкость, может быть представлена в виде:

где g = 9,81m/ c2 – ускорение свободного падения,
S - площадь пластины,
Глубина погружения пластины от a до b.
Путь, пройденный материальной точкой.. Если точка движется прямолинейно и ее скорость V = f{ t) - известная функция времени t то путь, пройденный материальной точкой за промежуток 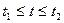 :
:

Пример 63.
Определить координаты центра тяжести сегмента параболы  отсекаемого прямой x = а .
отсекаемого прямой x = а .
В данном случае 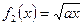 ,
, 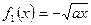
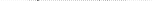
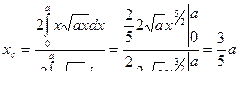
yс = 0, т. к. сегмент симметричен относительно оси ОХ.
Пример 64.
Найти координаты центра тяжести полуокружности х2+ у2 = а2, расположенной под осью ОХ.
 ;
; 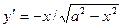 ;
; 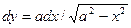
Абсцисса:
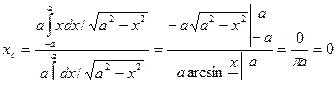
Ордината:
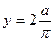
Пример 65.
Найти путь, пройденный точкой за 4с от начала движения со скоростью 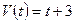 :
:
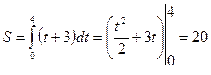
Приближенные вычисления определенных интегралов
Нам известно, что не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этом случае вычисление  по формуле Ньютона-Лейбница затруднительно, применяются различные методы приближенного вычисления.
по формуле Ньютона-Лейбница затруднительно, применяются различные методы приближенного вычисления.
Формула прямоугольников
Пусть на отрезке [а, b] задана непрерывная функция у = f( x)
требуется вычислить 
Разделим точками a = x0,xl,x2,...xn = b на n
Физические приложения определенного интеграла
В задачах, приводящих к понятию определенного интеграла, мы рассматривали работу по перемещению точки из a в b под действием переменной силы F. Сила направлена по оси ОХ и зависит только от x.
Сила давления жидкости Р плотности ρ на вертикальную пластинку, погруженную в жидкость, может быть представлена в виде:

где g = 9,81m/ c2 – ускорение свободного падения,
S - площадь пластины,
Глубина погружения пластины от a до b.
Путь, пройденный материальной точкой.. Если точка движется прямолинейно и ее скорость V = f{ t) - известная функция времени t то путь, пройденный материальной точкой за промежуток 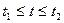 :
:

Пример 63.
Определить координаты центра тяжести сегмента параболы  отсекаемого прямой x = а .
отсекаемого прямой x = а .
В данном случае 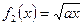 ,
, 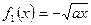
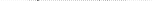
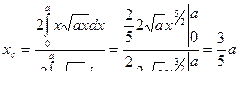
yс = 0, т. к. сегмент симметричен относительно оси ОХ.
Теорема 2. Интеграл вида 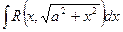 подстановкой
подстановкой
равных частей длины 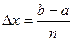
Обозначим через 
 Составим суммы
Составим суммы 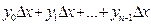 ,
,
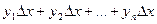 .
.
Каждая из этих сумм является интегральной суммой для функции f( x) на [a; b], и поэтому
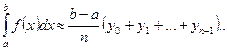
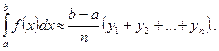
Геометрически:
Если функция f( x) > 0 и возрастающая, то вычисление по первой формуле приводит к площади ступенчатой фигуры, составленной из “входящих” прямоугольников, а если функция f( x) < 0 – по второй площадь ступенчатой фигуры, состоящих из “выходящих” прямоугольников.
Замечание. Ошибка, совершаемая по приведенным формулам, будет тем меньше, чем больше n, т. е. чем меньше шаг деления.
Формула трапеций
 Если данную кривую заменим вписанной ломаной вместо ступенчатой линии (как в формуле прямоугольников), то мы получим более точное значение
Если данную кривую заменим вписанной ломаной вместо ступенчатой линии (как в формуле прямоугольников), то мы получим более точное значение  Тогда площадь криволинейной трапеции аАВ b может быть заменена суммой площадей прямолинейных трапеций, ограниченных сверху хордами АА1, А1А2,...Ап-1В . Так как площадь первой трапеции
Тогда площадь криволинейной трапеции аАВ b может быть заменена суммой площадей прямолинейных трапеций, ограниченных сверху хордами АА1, А1А2,...Ап-1В . Так как площадь первой трапеции 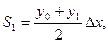 ,
,
площадь второй трапеции  и так далее, то
и так далее, то

или
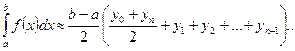
последняя формула носит название формулы трапеций.
Замечание. Чем больше n, и чем меньше будет шаг ∆x , тем с
большей точностью будет вычисление по формуле трапеций.
Формула парабол (Формула Симпсона)
 Разделим отрезок [а, b] на четное число частей n = 2 m. Площадь криволинейной трапеции, соответствующая первым двум отрезкам [x0, х1], [x1, х2] и ограниченной y= f( x), заменим площадью такой криволинейной трапеции, которая ограниченна параболой второй степени, проходящей через три точки: М1, М2, М3, и имеющей ось параллельную оси OY. Такую криволинейную трапецию будем называть параболической.
Разделим отрезок [а, b] на четное число частей n = 2 m. Площадь криволинейной трапеции, соответствующая первым двум отрезкам [x0, х1], [x1, х2] и ограниченной y= f( x), заменим площадью такой криволинейной трапеции, которая ограниченна параболой второй степени, проходящей через три точки: М1, М2, М3, и имеющей ось параллельную оси OY. Такую криволинейную трапецию будем называть параболической.
Уравнение параболы, параллельной оси ОУ: у = Ах2 + Вх + С. Коэффициенты А, В, С однозначно определяются из условия, что парабола проходит через три заданные точки. Аналогичные параболы строим и для других пар отрезков. Сумма параболических трапеций даст приближенное значение интеграла. Вычисляем вначале площадь одной параболической трапеции.
Лемма. Если криволинейная трапеция ограничена параболой
у = Ах2 + Вх + С, осью ОХ и двумя ординатами, расстояние между которыми равно 2 h, то ее площадь 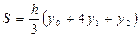 , где у0 и у2 – крайние ординаты, у1- ордината кривой в середине отрезка.
, где у0 и у2 – крайние ординаты, у1- ордината кривой в середине отрезка.
Доказательство.
Расположим вспомогательную систему координат так, чтобы х0 = – h , х1 = 0, х2 = h
75
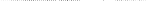 Коэффициенты в уравнении параболы у = Ах2 + Вх + С определяются из следующих уравнений:
Коэффициенты в уравнении параболы у = Ах2 + Вх + С определяются из следующих уравнений:

Считая коэффициенты А, В, С известными, определим площадь параболической трапеции с помощью определенного интеграла:
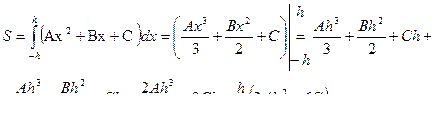
Но если в системе сложим все три уравнения, предварительно умножив y1 на 4, то получим у0 + 4у1 + у2 = 2 А h2 + 6С. Подставив полученное выражение в формулу определения площади параболической трапеции, получим:
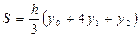
Вернемся к основной задаче. Воспользуемся полученной формулой, запишем приближенные равенства для h = ∆х :
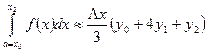

………………………………
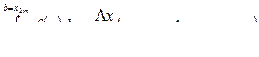
Складывая левые и правые части и пользуясь свойством определенного интеграла, получим: слева - исходный интеграл; справа - его приближенное значение:
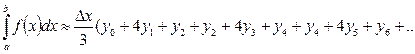

или
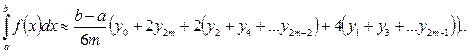
Полученная формула и есть формула Симпсона.
Замечание. Чем больше точек деления 2 m, тем точнее сумма в правой части равенства.
Пример 66
Вычислить 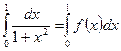
Разобьем участок 0 ≤ x≤ 1 на 10 частей, т. е. ∆х = 1 . Найдем значения функции.
| x | x2 | 1+ x2 | y = f(x) | x | x2 | 1+x2 | y = f(x) |
| 0,0 0,1 0,2 0,3 0,4 0,5 | 0,0 0,01 0,04 0,09 0,16 0,25 | 1,0 1,01 1,04 1,09 1,16 1,25 | 1,0000000 0,9900990 0,9615385 0,9174312 0,8620690 0,8000000 | 0,6 0,7 0,8 0,9 1,0 | 0,36 0,49 0,64 0,81 1,00 | 1,36 1,49 1,64 1,81 2,00 | 0,7352941 0,6711409 0,6097561 0,5534862 0,5000000 |
По формуле трапеций:

По формуле Симпсона (формуле парабол):
 +
+
+ 0,5524862) + 2(0,9615385 + ... + 0,6097561)) = 0,7853981
IIо формуле прямоугольников:


Так как 
Анализируя полученное решение, приходим к выводу, что расчеты по формуле прямоугольников дают точность1 знака после запятой, по формуле трапеции – 2 знака, по формуле Симпсона - 7 знаков.
Дата: 2018-12-28, просмотров: 379.