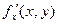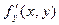Теорема. Если в некоторой окресности точки ( x, y) существуют частные производные и функции z= 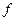( x, y) и эти производные непрерывны в самой точке ( x, y), то функция 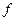( x, y) дифференцируема в этой точке.

Доказательство. Для любых Dx и Dy (не выходящих за пределы рассматриваемой окресности) имеем:

Dz=f(x+Dx,y+Dy)-f(x,y)=(f(x+Dx,y+Dy)-f(x,y+Dy))+(f(x,y+Dy)-f(x,y))

 Разность f(x+Dx,y+Dy)-f(x,y+Dy) можно рассматривать как приращение функции одной переменной Х: f(x,y+Dy) при переходе от x к x+Dx . Так как в каждой точке отрезка [x,x+Dx] (или [x+Dx,x] если Dx<0) эта функция имеет производную, совпадающую с 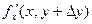, то по теореме Лагранжа получаем:

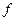(x+Dx,y+Dy)- 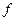(x,y+Dy)=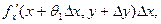

Где 0<q₁<1

Аналогично для второй разности получаем:

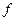(x,y+Dy)-f(x,y)=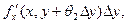

Где 0<q₂<1

Таким образом, 

Dz= (x+q₁Dx,y+Dy)Dx+ (x,y+q₂Dy)Dy, где 0<q_1,2<1

Функци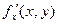и  и 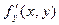непрерывны в точке (x,y), значит,              

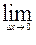
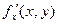                    (x+q₁Dx,y+Dy)=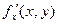

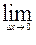
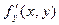                    (x,y+q₂Dy)=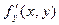  

т. е.  (x+q₁Dx,y+Dy)=  (x,y)+a₁,     (x,y+q₂Dy)= +a₂,

Где a₁ a₂ – бесконечно малые при. Dx 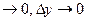.                                                    Подставляя эти значения в формулу (2) для Dz, пoлучаем

       Dz= 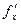 (x,y)Dx+ (x,y)Dy+a₁ Dx+a₂Dy,

Где a_{1 ,} a₂ –бесконечно малые при, Dx 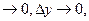а это и значит, что функция f(x,y) дифференцируема в точке (x,y).

 С помощью только что доказанной теоремы мы можем устанавливать дифференцируемость для широкого класса функций.

 Так, например, функция z=x² e^x2y3 в любой точке (x,y) дифференцируема, так как ее частные производные dz/dy=3x⁴ y² e^x2y3 и dz/dx=(2x+2x³ y³) e^x2y3 всюду непрерывны; функция z= 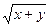дифференцируема в каждой точке полуплоскости x+y>0, так как там существуют и непрерывны ее частные производные dz/dy=dz/dx=1/(2 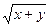), и т. д.

 Понятие дифференцируемости для функций трех и большего числа переменных вводится совершенно аналогично рассмотренномувыше случаю двух переменных.

 Функция u=f(x,y,z,…w) , определенная в некоторой окресности точки (x,y,z,…... w)n-мерного пространства, называется дифференцируемой в этой точке, если ее полное приращение в этой точке можно представить в виде:

Du=A(x,y,z,…. w)Dx+B(x,y,z,…. w)Dy+C(x,y,z,…. w)Dz+…..+

                 +M(x,y,z,…. w)Dw+a₁ Dx+a₂Dy+…+a_nDw

Где a₁…..a_n - бесконечно малые при Dx 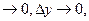Dz 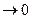,…..Dw 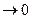. Слагаемое a₁Dx+a₂Dy+…+a_nDw    часто записывают в виде a*r, причем для дифференцируемой функции a 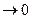при r= .

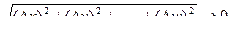Имеют место следующие необходимые (теорема1¢) и достаточные (теорема2¢) условия дифференцируемости.

 Теорема 1.

Функция f(x,y,z,…. w), дифференцируемая в точке (x,y,z,…. w) непрерывна в этой точке и имеет в ней частные производные по всем независимым переменным.

  Теорема 2.

Если функция f(x,y,z,… w) в некоторой окресности точки (x,y,z,…w) имеет частные производные по переменным x,y,z,…. w и если эти частные производные непрерывны в самой токе (x,y,z,…. w), то функция дифференцируема в этой точке.

 Функция (любого числа переменных), дифференцируема в каждой точке некоторой области, называется дифференцируемой в этой области.