Лекция 26. Первообразная, неопределенный интеграл, его свойства. Таблица интегралов.
Первообразная функция и неопределенный интеграл
Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Различные вопросы математики, естествознания и техники приводят к решению обратной задачи – восстановлению функции по заданным производной или дифференциалу.
Определение 1. Функция F( x) называется первообразной для функции f(х) на промежутке [a; b], если её производная F'[x) равна f(x) во всех точках этого промежутка, т.е. F'(x) = f(x)
Отыскание по данной функции f(х) её первообразной составляет одну из основных задач интегрального исчисления. Естественно, возникают вопросы: у всякой ли функции существует первообразная и, если существует, то одна или их много?
Ответ на первый вопрос вытекает из утверждения, что всякая непрерывная на [a; b] функция f(x) имеет первообразную.
В дальнейшем изложении, функции, для которых ищутся первообразные, будем считать непрерывными на [a; b], а данные конкретные элементарные функции будем рассматривать только на отрезке их непрерывности.
Ответ на второй вопрос исчерпывается утверждением: если функция f(х) имеет одну первообразную F( x), то она имеет их бесчисленное множество:
Лемма. Функция, производная которой на данном промежутке тождественно равна нулю, постоянна на этом промежутке.
Действительно, пусть для функции 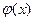 во всех точках
во всех точках  . Тогда для любых х1 и х2: по теореме Лагранжа
. Тогда для любых х1 и х2: по теореме Лагранжа 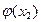 –
– 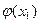 =
= 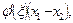 где
где 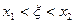 . Так как
. Так как  , то
, то 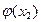 –
– 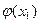 =0 и
=0 и 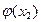 =
= 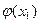 , т. е. функция, значения которой во всех точках одинаковы, постоянна:
, т. е. функция, значения которой во всех точках одинаковы, постоянна: 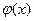 = const.
= const.
Теорема. Если F( x) – первообразная для f(х), то любая другая первообразная для f(х) (на том же промежутке) может быть записана в виде F( x) + С, где С - произвольная константа.
Доказательство.
Пусть Ф(х) произвольная первообразная для f(х) т. к. Ф'(х)= f(х), то для всех точек рассматриваемого промежутка
(Ф(х) – F( x))' =0 (на основании леммы), т. е.
(Ф(х) – F( x))' = Ф'(х) – F'( x) = f(х) – f(х) = 0
Значит, функция Ф(х) – F( x) постоянна на этом промежутке, т. е. |
Ф(х) – F( x) = С
или Ф(х) = F (х) + С.
Определение 2. Если функция F( x) является первообразной для f(х), то совокупность всех первообразных F( x) + С называется неопределенным интегралом от функции f(х):
 ,
,
где 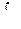 –- знак интеграла;
–- знак интеграла;
f(х) – подынтегральная функция,
f(х) dx – подынтегральное выражение
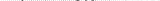 Геометрически: если у =
Геометрически: если у = 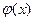 и у = F( x)
и у = F( x)
первообразные для f(х), то касательные
к их графикам в точках с общей
абсциссой х параллельны между собой
tg(α) = F'{x) = Ф'(х)
В таком случае расстояние между этими
кривыми, считая вдоль оси ОУ, остается
постоянным: Ф(х) – F( x))= С, т. е. эти кривые идут в некотором смысле "параллельно" друг другу.
Отыскание первообразной и отыскание неопределенного интеграла от функции называется интегрированием этой функция. Чтобы проверить правильность интегрирования достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Основные свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции
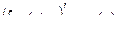
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
3. Неопределенный интеграл от производной равен самой функции плюс произвольная константа

4. Неопределенный интеграл от дифференциала равен дифференцируемой функции плюс константа

5. Постоянный множитель можно выносить за знак интеграла

6. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен сумме интегралов от этих функций (если они существуют)
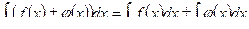
При вычислении неопределенных интегралов полезно иметь в виду следующие правила:
1. Если  , то
, то 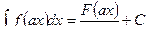
2. Если  , то
, то 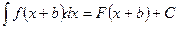
3.  Если
Если  , то
, то 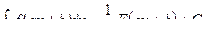
Основная таблица интегралов
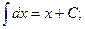
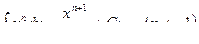
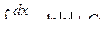

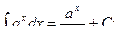


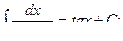

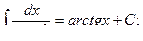
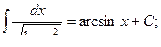
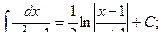
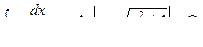

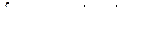
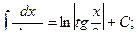
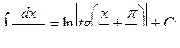

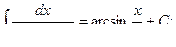
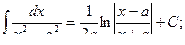
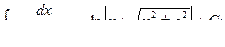
Пример 1

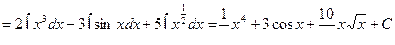
Здесь применили основные свойства интегралов и таблицу интегралов, выполнили непосредственное интегрирование.
Дата: 2018-12-28, просмотров: 409.