Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Функция z=f(x, y), определенная в некоторой окрестности точки (x₀,y₀), называется непрерывной в этой точке, если

       Геометрически это означает, что при приближении точки М(x, y) по любой последовательности точек к точке М₀(х₀, у₀) аппликаты соответ­ст­вующих точек поверхности, изображающей функцию z=f(x, y), стре­мятся к аппликате поверхности в точке М₀.

       В дальнейшем нам часто придется пользоваться следующим эквива­лентным данному выше определением непрерывности функции: функция f(x, y) называется непрерывной в точке (х₀, у₀), если для любого положи­тельного числа ε существует число δ>0, такое, что для всех точек (х, у), удовлетворяющих условию 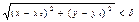,                                  выполнено неравен­ство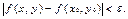

       Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что для функций двух переменных сумма и произведение двух непрерывных функций есть непрерывная функция; частное двух не­прерывных функций есть непрерывная функция в точках, в которых зна­менатель отличен от нуля; сложная функция, составленная из нескольких непрерывных функций, есть непрерывная функция и т. д.

       Например, функции f(x, y)=x²+y², φ(x, y)=e^x+y, F(x, y)=sin(x³y³+x-y+1) непрерывны всюду, функция R(x, y)=(x²+y²-1)/(x-y) непрерывна, всюду кроме точек прямой х=у, и т. д.

       Если функция f(x, y) определена в окрестности точки М₀(х₀, у₀) (кроме, может быть, самой точки М₀) и не являются непрерывной в этой точке, будем называть ее разрывной в точке М₀.

       Например:    

1) функция 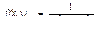разрывна в точке (0, 0), так как она определена всюду, кроме этой точки

       2) функция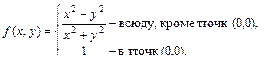

будет разрывна в точке (0, 0), так как не существует предела этой функции при х→0, у→0;

3) функция

в точке (1, 2) разрывна, так как

Ранее мы рассматривали свойства функций, непрерывных на от­резках (теоремы об ограничениях функции, о достижении наибольших и наи­меньших значений и т. д.). Аналогичные свойства имеют место для непре­рывных функций двух переменных, если их рассматривать в так на­зывае­мых замкнутых ограниченных областях, являющихся двухмерным анало­гом отрезка. Для того чтобы сформулировать эти свойства, введем ряд оп­ределений для множества точек плоскости ХОY.

                                           Рисунок 10

Множество точек плоскости называется связным, если любые две точки этого множества соединить непрерывной кривой, состоящей из то­чек того же множества.

4) связным будет множество точек внутри круга, множество точек любой дуги l эллипса, множества точек кольца 1≤х²+у²≤4 (рис. 10) и т. д.

                                      Рисунок 11

5) Множество точек, состоящее из трех отдельных точек, не будет связным. Несвязным будет также множество точек, принадлежащих двум кругам: х²+у²≤1 и (х-2,3)²+у²≤1 (рис. 11) и т. д.

Точка М называется внутренней точкой некоторого множества, если существует окрестность этой точки, состоящая из точек данного множе­ства.

      Рисунок 12        Рисунок 13       Рисунок 14

Множество, каждая точка которого – внутренняя, называется откры­тым множеством.

6) Открытыми будут множества всех точек, лежащих внутри круга, внутри двух непересекающихся кругов ( рис. 12). Откры­тым будет множе­ство всех точек плоскости, лежащих вправо от оси OY ( рис.13).

Множество точек прямоугольника -1≤х≤1, -2≤у≤2 открытым не будет, так как принадлежащие ему точки прямых х =±1, у =±2 не яв­ляются внут­ренними ( рис. 13).

 Связное открытое множество точек плоскости называется  обла­стью. Примеры областей: множества точек, лежащих внутри круга, пря­моугольника, множество точек кольца 1<х² + у²<4, множество точек (х,у ) плоскости, для которых х> 0, у> 0 ( рис.13).

 Точка М называется граничной точкой области, если в любой ее ок­рестности есть точки как принадлежащие, так и не принадлежащие этой области. Совокупность всех граничных точек области называется ее гра­ницей. Так, например, для области, состоящей из точек, лежащих внутри эллипса, границей будет сам эллипс.

                                         Рисунок 15