Рассмотрим последовательность точек М1(х1, у1,),М2(х2, у2),…, Мп (хп,уп),… плоскости ХОY. Будем говорить, что эта последовательность точек сходится к точке М0(х0, у0), если расстояние

стремится к нулю при п→∞1).
Совокупность точек плоскости, находящихся от точки М0 на расстоянии, меньшем δ,т.е. внутренность круга с центром М0 радиуса δ называется δ-окрестностью точки М0.
Таким образом, последовательность точек М1, М2,…, Мп,… плоскости называется сходящейся к точке М0, если в любой окрестности точки М0 лежат все точки последовательности, начиная с некоторого номера.
Обобщая данное ранее определение предела функции одной переменной с помощью предела числовой последовательности, дадим определение предела функции двух переменных.
Пусть функция z = f (х, у) задана в некоторой окрестности точки М0, кроме, быть может, самой этой точки.
Если для любой последовательности точек М1(х1, у1,),М2(х2, у2),…, Мп(хп,уп),… этой окрестности, сходящейся к точке М0 (х0, у0), соответствующая последовательность значений функции f1 (х1, у1), f2 (х2, у2), … , f (хп, уп),… имеет пределом одно и то же число А, то это число А называют пределом функции f (х, у) при х→х0 , у→у0 и пишут:
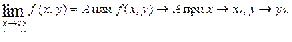
 Так, например, функция f (х, у) = х2 + у2 определена во всей плоскости. Рассмотрим точку М0(1,2). Для любой последовательности точек (х1, у1), (х2, у2),…, (хп, уп),…, сходящейся к этой точке М0, имеем:
Так, например, функция f (х, у) = х2 + у2 определена во всей плоскости. Рассмотрим точку М0(1,2). Для любой последовательности точек (х1, у1), (х2, у2),…, (хп, уп),…, сходящейся к этой точке М0, имеем:
 |
следовательно,
Геометрически тот факт, что число А является пределом функции f(х,у) при х→х0, у→у0, означает, что, какова бы ни была последовательность точек плоскости М1, М2,…, Мп,…, неограниченно приближающихся к точке М0, последовательность аппликат соответствующих им точек поверхности, изображающей функцию z = f (х, у), имеет пределом число А. При этом в самой точке М0 функция может быть не определена, а может быть определена и имеет любое значение, как равное А, так и отличное от него. Предел функции z = f (х, у) при х→х0, у→у0 определяется поведением функции вблизи точки (х0, у0) и не зависит от значения функции в самой этой точке.
В рассмотренном выше примере мы имели:
f ( х, у) = х²+ у²,
для функции же φ(х, у), определяемой равенствами
φ(1, 2)=7, тогда как предел функции φ(х, у) при х→1, у→2 равен пределу функции f(x, y).
 Приведем теперь пример функции, не имеющей предела при х→х0, у→у0.
Приведем теперь пример функции, не имеющей предела при х→х0, у→у0.
Функция , определена всюду, кроме начала координат, при х→0, у→0
предела не имеет, так как, выбирая две сходящихся к точке О(0,0) последовательность точек (х1, 0) (х2, 0), …, (хп, 0), … и (0, у1), (0, у2), …, (0, уп), …, получим
Так же как для функции одной переменной, можно показать, что данное выше определение предела функции двух переменных эквивалентно следующему определению предела: число А называется пределом функции f(x, y) при х→х0, у→у0, если для любого положительного числа ε существует число δ, δ>0, такое, что для всех точек (х,у), отличных от точки (х0,у0) и удовлетворяющих условию  выполнено неравенство
выполнено неравенство
 |
Геометрически это значит, что, каково бы ни было число ε>0, найдется столь малая δ-окрестность точки М0(х0, у0), что во всех ее точках М(х, у), отличных от М0, аппликаты соответствующих точек поверхности, изображающей функцию z=f(x, y), отличаются от числа А по абсолютной величине меньше, чем на ε.
Величина δ зависит от ε и при ε, стремящимся к нулю, δ, вообще говоря, также стремится к нулю.
Будем называть функцию f(x, y) бесконечно малой при х→х0, у→у0, если
Пользуясь любым из определений предела функции двух переменных, можно вывести основные свойства бесконечно малых функций, дать понятие порядка, эквивалентности бесконечно малых; доказать теорему о том, что разность между функцией, имеющей предел и ее пределом есть бесконечно малая функция; доказать основные теоремы об арифметических операциях над пределами. Доказательства этих теорем аналогичны соответствующим доказательствам для функций одной переменной.
Не останавливаясь на понятиях бесконечного предела функции двух переменных, отметим, что в дальнейшем, говоря о пределах, мы будем иметь в виду конечный предел.
Данные выше определения без труда обобщаются на функции трех и более переменных, теряется лишь их геометрическая наглядность.
Так, например, δ–окрестностью точки (х0, у0, z0, …, ω0) п-мерного пространства называется совокупностью точек (х, у, z, ω), находящихся от точки (х0, у0, z0, ω0) на расстоянии, меньшем δ.
В случае п=3 δ-окрестность точки (х0, у0, z0) представляет собой внутренность шара радиуса δ с центром в этой точке.
Для функции f(x, y, z, …, ω), определенной в некоторой окрестности точки (x0, y0, z0, …, ω0) (кроме, быть может, этой точке), можно дать, например, следующее определение предела. Число А называется пределом функции f(x, y, z, …, ω) при х→х0, у→у0, z→z0, …, ω→ω0, если для любого числа ε>0 существует число δ>0, такое, что, для всех точек (x, y, z, …, ω) указанной окрестности , отличных от точки (x0, y0, z0, …, ω0) удовлетворяющих условию
выполнено неравенство
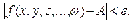
Дата: 2018-12-28, просмотров: 392.