Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

До сих пор мы занимались изу­че­нием функций одной переменной, т. е. Изуче­нием переменной, значе­ния кото­рой зави­сят от зна­чений одной независи­мой пере­менной.

       На практике часто приходится иметь дело с величинами, числен­ные значения ко­торых зави­сят от значений нескольких изме­няю­щихся не­зави­симо друг от друга физиче­ских и геометри­ческих вели­чин. Изучение таких

величин приводит к понятию функ­ции не­сколь­ких переменных.

       Начнем с простейшего случая, когда таких переменных две.

       Переменная z называется функцией двух переменных х и у, если каж­дой паре чисел (х, у) из не­которого множества по определен­ному правилу или закону ста­вится в соответ­ствие одно или несколько значений пере­менной z.

       При этом переменные х и у на­зыва­ются независимыми перемен­ными, или ар­гумен­тами, а перемен­ная z – зависимой перемен­ной, или функцией.

       Множество пар чисел (х, у), для ко­то­рых определена функция z, на­зы­вается обла­стью определения этой функции.

       Множество значений функции z на­зыва­ется областью изменения этой функ­ции.

       В математическом анализе обычно рас­сматриваются действи­тельные

функции двух переменных, т. е. функции, при­нимающие действи­тельные значения на множе­стве пар действительных чисел ¹).

       Если каждой паре чисел (х, у) из об­ласти определения функции соот­ветст­вует одно зна­чение – однозначной, в против­ном случае -  многознач­ной. Так же как и для функций одной перемен­ной, если не ого­ворено противное, мы будем предпола­гать, что рассматривае­мые функции двух пере­менных одно­значны.

       Тот факт, что переменная z яв­ляется функ­цией переменных х и у, обычно за­писы­вают в виде:

           

Буквы          и другие ис­пользо­ваны для обозначения закона соот­ветст­вия ме­жду незави­симыми переменными х и у и зависи­мой пе­ре­мен­ной z. Частное значе­ние функ­ции                    

при х=х₀, у=у₀  обычно запи­ сывают в виде: f(х₀, у₀) или              .

 

       Сам закон соответствия может быть задан произвольным образом (аналитиче­ски, т. е. с помощью формул, выражаю­щих z че­рез х и у, таб­лично, графически, сло­весным образом и пр.).

       Математический анализ изу­чает пре­иму­щественно аналитиче­ски за­дан­ные функции.

       Рассмотрим несколько приме­ров та­ких функций.

       1. Если х и  у могут принимать лю­бые чи­словые значения, то пере­менные z=x²+y², z=ln(1+x⁴+y⁵) и т. д. представ­ляют собой анали­тиче­ски заданные функции от х и у.

       Область определения каждой из них – множество всевозможных пар чисел (х, у).

       2. Объем конуса V есть функ­ция его вы­соты H и радиуса основа­ния R.

Ее аналитическое выражение:                 . Об­ласть определения – все­воз­можные пары чисел (R, H), где R>0, H>0.

       Естественной областью опре­деле­ния ана­литически заданной функ­ции z=f(x, y) называ­ется сово­купность всех пар чисел (х, у), кото­рым соот­ветствуют действительные значения функции. Так, например, для функции z=ln(x²+y²-1) ес­тест­венная об­ласть определения состоит из всех пар чи­сел (х, у), для которых х²+у²-1>0, т. е. х²+у²>1, а для функ­ции

                             естественная область опре­деления состоит из всех пар чисел, для которых

           

Рассмотренная в примере 2 функция                имеет естест­венной областью определе­ния мно­жество всевозможных пар чисел (R, H).

В дальнейшем, если дополни­тель­ные огра­ничения на изменение неза­виси­мых пе­ремен­ных постанов­кой задачи (как это было в при­мере 2) не накладываются, под обла­стью опре­деления аналитически за­данной функ­ции будем подразумевать ее естествен­ную область опреде­ления.

Выберем на плоскости прямо­угольную систему координат ХОY и бу­дем изображать                     

        Рисунок 1           пары чи­сел (х, у) точками плоскости с коор­ди­натами х, у. То­гда область опре­деления функции f(x, y) бу­дет изо­бражаться некоторым множеством точек М плоскости, в связи с чем функцию двух переменных часто называют функцией точки М плос­кости и обозначают z=f(M), а ее об­ласть определения отождествляют с мно­жеством изобра­жающих ее то­чек.

Так, для функции z=ln(x²+y²-1) область определения изображается множе­ством то­чек плоскости XOY, лежащих вне круга К с центром (0, 0) радиуса 1, поэтому мы будем го­ворить: функция z=ln(x²+y²-1) опре­делена вне круга К (см. рис. 1).

       У функции                                 об­ласть определения изображается множест­вом точек прямоугольника со сторонами х=±1, у=±2, поэтому мы будем говорить: функция                                 определена в прямоуголь­нике со сторонами х=±1, у=±2 (рис. 2).

       Как известно, функция одной перемен­ной может быть изображена некоторой кри­вой на плоскости, если рассматривать значе­ния ее ар­гу­мента как абсциссы, а значения функции как ординаты точек кри­вой.

       Подобным образом функция двух пере­менных z=f(x, y) может быть геометрически изображена в виде поверхности.

       Рассмотрим в пространстве прямоугольную систему координат XYZ. Область определения функции z=f(x, y) изображается некоторым множест­вом точек плоскости XOY. Каждой точке М₀(х₀, у₀) этого мно­жества поста­вим в соответствие точку пространства N₀(x₀, y₀, z₀), аппликата которой

           Рисунок 2                        Рисунок 3                     Рисунок 4

равна значению функции в точке М₀: z₀=f(x₀, y₀).Совокупность всех таких точек представляет собой не­которую поверхность. Ее естест­венно принять за графическое изо­бражение функции z=f(x, y) (рис. 3). Итак, графиком функции z=f(x, y) в пространстве XYZ является поверх­ность, представ­ляю­щая собой гео­метрическое место точек (х, у, f(х, у)), когда точка (х, у) про­бегает об­ласть определения функции.

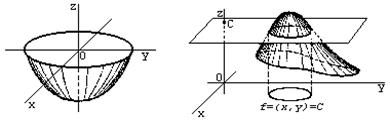
      Рисунок 5                                Рисунок 6

       Например, для функции z=x²+y² область определения – вся плоскость, а изображающая ее по­верхность – параболоид вращения (рис. 4); функция

                        имеет областью определения круг           и изобра­жа­ется нижней полусферой с центром О (0, 0, 0) радиуса R=1 (рис. 5).

       Познакомимся еще с одним способом геометрической иллюст­рации функций двух переменных. Будем называть линией уровня функции z=f(x,y) геометрическое место точек (х, у) плоскости, в кото­рых функция принимает одно и то же значение С.

       Линию уровня можно постро­ить, спроектировав на плоскость XOY множество точек пространства XYZ, лежащих в пересечении по­верхно­сти изображающей функцию z=f(x, y), и плоскости z=C (рис. 6).

       Уравнение линии уровня имеет вид: f(x, y)=C. Изменяя С, мы будем получать различные линии уровня для данной функции.

       Если положить С=С₁, С₂,…,Сп,…, выбрав эти числа в арифметиче­ской прогрессии с разностью h, то мы получим ряд линий уровня, по вза­имному рас­положению которых можно су­дить о характере изменения функции (рис. 7). В частности, там, где линии гуще, функция изменяется быстрее (поверхность, изображающая функцию, идет круче), а там, где линии уровня располагаются реже, функция изменяется медленнее (со­от­ветствующая поверхность будет более пологой). Кроме того, от­метки на линиях уровня дают непо­средственно значения функции в точках этих линий. Выбирая h дос­таточно малым, можно таким обра­зом получить до­вольно точное представление о поведении функ­ции.

                       Рисунок 7

Рассмотрим несколько примеров.

1. Функция z=x²+y² имеет линиями окружности х²+у²=С, 0≤С<+∞.

Полагая, например, С=0, 1, 2, 3,…, получаем соответствующие линии уровня, сгущающиеся с ростом С. при С=0 окружность вырождается в точку (0, 0) (рис. 8).

       Для функции z=x+y линиями уровня будут прямые х+у=С, -∞<С<+∞. Пола­гая С=0, ±1, ±2, …, получаем ряд линий уровня (рис. 9).

Линии уровня часто используются при составлении географических карт (линии уровня – линии, в которых высота точек земной поверхности над уровнем моря одинакова), при составлении метеорологических карт (линии уровня – линии одинаковых температур (изотермы), линии равного давления (изобары)) и т. д.

    Рисунок 8                                        Рисунок 9

Понятие функции трех переменных дается аналогично случаю двух переменных.

Переменная и называется функцией трех переменных х, у, z ¹), если каждой тройке чисел (x, y, z) из некоторого множества по определенному правилу или закону ставится в соответствие одно или несколько значений переменной и. При этом х ,у и z называются независимыми переменными, или  аргументами, а и – зависимой переменной, или  функцией.

Областью определения такой функции называют множество всех рассматриваемых троек чисел. Если функция задана аналитически, с по­мощью формул, то под ее  естественной областью определения подразу­мевают совокупность всех тех троек чисел (х, у, z), для которых функция принимает действительные значения.

 Изображая тройки чисел (х, у, z)  точками пространства ХYZ, мы мо­жем рассматривать функцию трех переменных u=f (х, у, z) как функцию точки  М (х, у, z)  пространства, а область определения функции трех пере­менных – как некоторое множество точек пространства.

Так, например функция 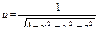  определена для тех

точек про­странства, координаты которых удовлетворяют неравенству   4 – х² – у² – z²>0, т.е. определена внутри сферы х² + у² + z² = 4, а функция  и=х + у + z  определена во всем пространстве.

Изобразить функцию трех переменных с помощью графика в трех­мерном пространстве нельзя. Для наглядного изучения функций трех пе­ременных используются так называемые поверхности уровня функции.

Поверхностью уровня функции и= f (х, у, z) называют геометриче­ское место точек пространства, в которых функция принимает одно и то же значение С. Уравнение поверхности уровня: f (х, у, z)= С. Изменяя  С, получаем различные поверхности уровня. По их взаимному расположе­нию можно судить о характере поведения функции.

Определения функций двух и трех переменных легко переносятся на случай любого числа переменных. А именно, переменная  и называется  функцией п переменных х, у, z, …, ω, если каждой системе из п чисел (х, у, z,…, ω) из некоторого множества по определенному правилу или за­кону ставится в соответствие одно или несколько значений переменной и. При этом переменные х, у, z,…, ω называются независимыми перемен­ными,  или  аргументами, а переменная и – зависимой переменной, или  функ­цией. Множество рассматриваемых систем из п  чисел называется  обла­стью определения функции. Обозначаются функции п переменных в виде :  и= f ( х, у, z,…, ω), и=F(х,у,z,…, ω), и=и (х, у, z,…, ω)  и т.д.

Так же как для п=2 и  п=3, функции любого числа п переменных удобно рас­сматривать как функции точки п-мерного пространства. Будем называть точкой М п-мерного пространства всякую систему из п чисел (х, у, z,…,w). Сами числа х, у, z,…,w называются при этом координатами  точки М. Совокупность всех таких точек составляет п-мерное пространство.

Расстояние  между любыми двумя точками М₁ (х, у,z,…,w) и М₂ (х, у, z,…,w)  этого пространства определяется по формуле

При п=1, 2, 3 это «расстояние» совпадает с обычным. В п-мерном простран­стве можно ввести понятия «прямых», кривых и пр., так чтобы при п=2, 3, как ча­стный случай, получались обычные определения.

Например, прямой, проходящей через точки М₁ (х₁, у₁, z₁,…,ω₁)  и М₂ (х₂, у₂, z₂,…,ω₂)   называют геомет­рическое место точек (х, у, z,…,ω),  координаты которых удовлетворяют уравне­ниям:

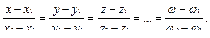
Обозначая эти отношения через t, получаем уравнения той же прямой в пара­метрической форме:

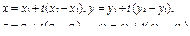
 Непрерывной кривой  в п-мерном пространстве называется любое геометри­ческое место точек М (х, у, z,…,w),  координаты которых удовлетворяют уравне­ниям:

    х = х ( t ), у = у ( t ), z = z ( t ), …, ω = ω ( t),

 

где  х (t), у (t), z (t),…, ω (t) – непрерывные функции параметра t, изменяюще­гося в некоторых переделах.

Мы будем в дальнейшем подробно рассматривать лишь функции двух переменных, имея в виду, что перенос полученных определений и резуль­татов на функции трех и более переменных представляется собой, как пра­вило, лишь технические трудности.