Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Линии второго порядка. Эллипс. Гипербола. Парабола.

Эллипс представляет собой результат равномерной деформации окружности вдоль одного из ее диаметров.

Определение. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.

F1 и F2 – фокусы эллипса, F1(-c; 0); F2(c;0). Расстояние между ними - 2С. Возьмем произвольную точку эллипса M(x, y). Обозначим F1M=r1 F2M=r2. Тогда

F₁M+F₂M=r₁+r₂=2a, где

 

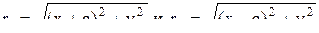- фокальные радиусы точки М.

Каноническое уравнение эллипса:

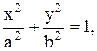                                                                 (12.1)

где b²=a²-c².

Это уравнение второй степени Þ эллипс есть линия второго порядка. Эллипс симметричен относительно обеих осей координат.

Определение. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси

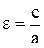                                                                  (12.2)

Так как c<a, то e<1.

Эксцентриситет характеризует форму эллипса. Чем больше эксцентриситет, тем более эллипс вытянут (в случае окружности b =a и e=0).

Определение. Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии 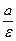 от него, называются директрисами эллипса.

Уравнения директрис: 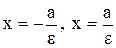   ,                                                          (12.3)

Пример 1. Найти полуоси, координаты фокусов и эксцентриситет эллипса

x²+2y²=8.

Решение. Приведем уравнение эллипса к каноническому виду, для этого разделим обе части уравнения на 8:

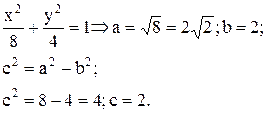
Таким образом

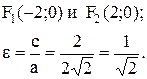
Пример 2. Написать каноническое уравнение эллипса, длина малой оси которого равна 6, а фокусное расстояние равно 8:

2b=6;                     2c=8.

Решение:

2b=6 Þ b=3

Известно, что 2c=8 Þ c=4.

a²=b²+c²; a²=9+16=25,

запишем уравнение эллипса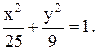

Определение. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.

 

 

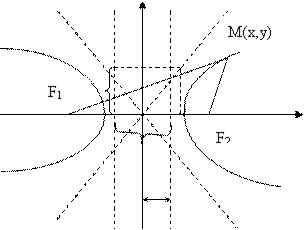
F1(-c; 0) и F2(c;0) – фокусы; М(x, y) – произвольная точка гиперболы. F1M=r1; F2M =r2 - фокальные радиусы F1F2=2c; ,

                  

 

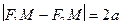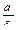
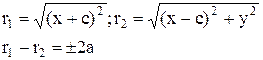
Каноническое уравнение гиперболы:

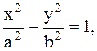                                                                                        (12.4)

где b²=c²-a².

Гипербола - линия второго порядка, симметричная относительно осей координат.

Определение. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами.

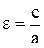                                                       (12.5)

так как c>a, то e>1.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах (A₁ и A₂), называется основным прямоугольником гиперболы.

Эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а значит, и форму гиперболы: чем меньше эксцентриситет, тем больше вытянут основной прямоугольник.

Определение. Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположенные симметрично относительно центра на расстоянии 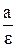 от него, называются директрисами гиперболы.

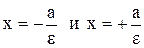                                                                 (12.6)

Ветви гиперболы (12.4) сколь угодно близко приближаются к прямым

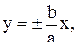                                              (12.7)

которые называются асимптотами гиперболы.

Две гиперболы, которые определяются уравнениями

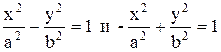называются сопряженными.

Гипербола с равными полуосями (a = b) называется равносторонней; ее каноническое уравнение имеет вид x²-y²=a²  или -x²+y²=a².

Пример 1. Дана гипербола 16x²-9y²=144.

Найти: 1) полуоси a и b;

2) фокусы;

3) эксцентриситет;

4) уравнения асимптот;

5) уравнения директрис.

Решение.

1) Приведем уравнение гиперболы к каноническому виду, разделив обе части уравнения на 144. Получим:

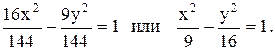
Тогда a=3; b=4.

2) Зная полуоси a и b, можем найти c из соотношения

b²=c²-a²

16=c²-9

c²=25

c=5.

Тогда фокусы данной гиперболы имеют координаты

F₁(-5,0) и F₂(5,0).

3) Эксцентриситет теперь легко определить по формуле (4.5) .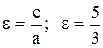

4) Уравнения асимптот по (15.7)

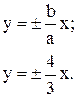
5) Уравнения директрис по (12.6)

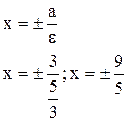
Пример 2. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

1) ее оси 2а=10 и 2b=8;

2) расстояние между фокусами 2с=10 и ось 2b=8;

3) расстояние между фокусами 2с=6 и эксцентриситет e=3/2;

4) ось 2а=16 и эксцентриситет e=5/4;

5) уравнения асимптот y=±4/3x и расстояние между фокусами 2с=20;

6) расстояние между директрисами равно 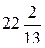 и расстояние между фокусами 2с=26.

Решение:

1) 2а=10 и 2b=8.             Откуда а=5; b=4.

Уравнение гиперболы: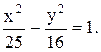             

2) 2с=10 и 2b=8. Þ c=5; b=4.

Из b²=c²-a² найдем a:

16=25-а²; а²=25-16

а²=9;          а=3.

Уравнение гиперболы: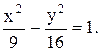             

3) 2с=6 и e=3/2.

c=3;

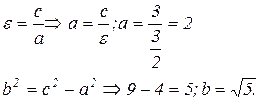
Уравнение гиперболы: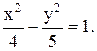             

4) 2а=16 и e=5/4

а=8 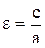       Þ 5/4 = c/8 Þ c=10

b²=c²-a²=100-64=36; b=6

Уравнение гиперболы: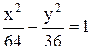             

5)

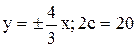
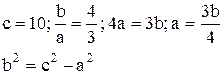
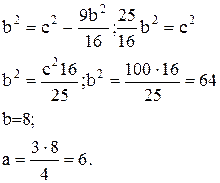
Уравнение гиперболы: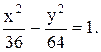             

6) 2с=26; ;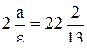

с=13;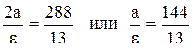

13а=144e, а e=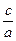

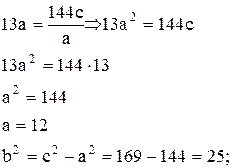
Уравнение гиперболы:              .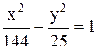

Определение. Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.

Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой p. Число p называется параметром параболы.

y

Возьмем произвольную точку параболы M(x,y).

Обозначим FM = r, d - расстояние до директрисы

x