Уравнение прямой. Основные задачи на прямую.
Определение. Уравнение F(x,y) = 0 (11.1), которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней, называется уравнением данной линии.
Если x и y входят в уравнение (11.1) линейно, то уравнение (11.1) представляет прямую линию на плоскости; (например y=3x+5); если x и y (или хотя бы одна из переменных входят в уравнение (11.1) в квадрате, то уравнение (11.1) представляет линию второго порядка (например y=x2).
Определение. Уравнение вида Ax+By+C=0 (12.2) называется общим уравнением прямой.
Определение. Уравнение y =kx + b (11.3) называется уравнением прямой с угловым коэффициентом, где
k - угловой коэффициент;
b - величина отрезка, который отсекает прямая на оси OY, считая от начала координат;
k = tg a, где a - угол наклона прямой к оси OX

Если прямая задана общим уравнением Ax+By+C=0, то ее угловой коэффициент определяется по формуле
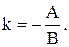 (11.4)
(11.4)
Уравнение y-y0 = k(x-x0) (11.5)
является уравнением прямой, проходящей через точку M(x0;y0) и имеющей угловой коэффициент k.
Уравнение 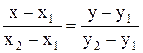 (11.6)
(11.6)
является уравнением прямой, проходящей через две точки M1(x1; y1) и M2(x2; y2).
Признаком параллельности двух прямых является равенство их угловых коэффициентов k1=k2.
Признаком перпендикулярности двух прямых является соотношение
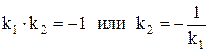 .
.
Пример. Составить уравнение прямой, проходящей через точки A(2;3) и B(5;1).
Решение.
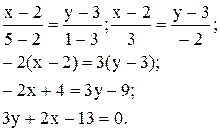
Пример. Дана прямая 2x+3y+4=0.
Составить уравнение прямой, проходящей через точку M0(2;1):
а) параллельно данной прямой;
б) перпендикулярно к данной прямой.
Решение. Определим по формуле (12.4) угловой коэффициент данной прямой 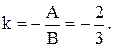
Составим уравнение прямой, проходящей через точку M0 и имеющей угловой коэффициент k1:
y-1=k1(x-2).
а) Для того, чтобы найденная прямая y-1=k1(x-2) была параллельна данной 2x+3y+4=0 необходимо выполнение равенства k=k1.
Таким образом, уравнение прямой, проходящей через точку M0 и параллельной данной будет иметь такой вид:
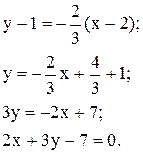
б) Для того, чтобы найденная прямая y-1=k1(x-2) была перпендикулярна к данной прямой, необходимо выполнение равенства k × k1= -1
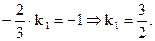
Таким образом, уравнение прямой, проходящей через точку M0 и перпендикулярной к данной прямой, будет таким:
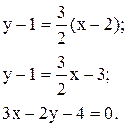
Пример. Составить уравнение прямой, проходящей через точку A(2; 3) и перпендикулярной прямой
4x+3y-12=0.
Решение. Составим уравнение прямой, проходящей через точку A(2; 3) под углом a
y-3=k2(x-2), где k2=tga.
Угловой коэффициент данной прямой k1=-4/3.
Учитывая, что угловые коэффициенты перпендикулярных прямых связаны соотношением
k1×k2=-1, получаем -4/3×k2= -1, откуда k2=3/4.
Подставляя k2 в полученное уравнение, выпишем уравнение прямой
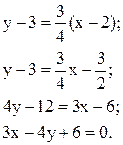
Уравнение прямой “в отрезках”
Если ни один из коэффициентов уравнения (12.2) не равен нулю, то его можно преобразовать к виду
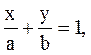 (11.7)
(11.7)
где 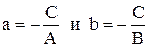 - величины отрезков, которые отсекает прямая на координатных осях.
- величины отрезков, которые отсекает прямая на координатных осях.
Это уравнение (11.7) называется уравнением прямой“ в отрезках”.
Этим уравнением пользуются для построения прямой.
Поэтому при необходимости уравнение прямой приводят к виду уравнения “в отрезках” и строят прямую.
Пример. Построить прямую 5x-3y=-15.
Решение.
Преобразуем это уравнение в уравнение прямой в “отрезках”. Для этого разделим обе части уравнения на -15. Получим
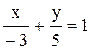
На оси абсцисс откладываем отрезок, величина которого равна a= -3 единицы, на оси ординат b=5 единиц и соединим их концы.
Уравнение прямой, проходящей через данную точку M 1 ( x 1 ; y 1 )
и имеющей заданный нормальный вектор
Определение. Любой ненулевой вектор 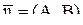 , перпендикулярный данной прямой, называется нормальным вектором этой прямой.
, перпендикулярный данной прямой, называется нормальным вектором этой прямой.
Пример. Составить уравнение прямой, проходящей через точку M1(2; 3) и имеющей нормальный вектор 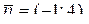
Решение. Запишем уравнение искомой прямой, подставив данные в (11.8):
-1(x-2)+4(y-3)=0;
-x+2+4y-12=0;
x-4y+10-0.
Определение. Любой ненулевой вектор 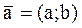 , коллинеарный данной прямой, называется направляющим вектором этой прямой.
, коллинеарный данной прямой, называется направляющим вектором этой прямой.
Уравнение прямой, проходящей через данную точку M1(x1, y1) и имеющей заданный направляющий вектор, имеет вид:
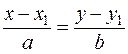 (11.9)
(11.9)
Пример. Составить уравнение прямой, проходящей через точку А(2; -1) и имеющей направляющий вектор 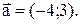
Решение. Подставим данные своего примера в (11.9) и получим:
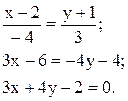
Параллельность прямых
Пусть на плоскости заданы две прямые
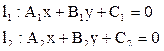
Нормальные векторы этих прямых имеют координаты
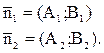
Если l1 êêl2, то их нормальные векторы коллинеарны Þ 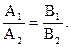
Если 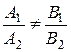 , то прямые различны, не параллельны друг другу, а значит пересекаются в одной точке (l1Il2).
, то прямые различны, не параллельны друг другу, а значит пересекаются в одной точке (l1Il2).
Если 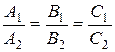 , то оба уравнения определяют одну и ту же прямую l1=l2.
, то оба уравнения определяют одну и ту же прямую l1=l2.
Пример. Установить, параллельны ли прямые?
а) 4x-6y+10=0 и 6x-9y+2=0.
Решение. Составляем соотношение
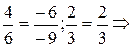 прямые параллельны;
прямые параллельны;
б) 6x-3y-2=0 и 4x-10y+6=0.
Решение: 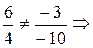 прямые не параллельны.
прямые не параллельны.
Перпендикулярность прямых
Если l1^l2, то скалярное произведение нормальных векторов этих прямых должно быть равно нулю, т.е. 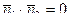 A1A2+B1B2=0.
A1A2+B1B2=0.
Пример. Установить, перпендикулярны ли прямые 5x-2y+1=0 и 4x+10y-1=0?
Решение.
5×4+(-2)×10=0
20-20=0 Þ прямые перпендикулярны.
Угол между двумя прямыми
Определение. Углом между двумя прямыми называется величина меньшего из углов, образованного этими прямыми.
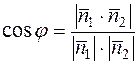 , где
, где 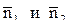 - нормальные векторы прямых l1 и l2 (11.10)
- нормальные векторы прямых l1 и l2 (11.10)
Пример. Найти угол между двумя прямыми
2x-3y+4=0 и x+5y-3=0.
Решение. Найдем координаты нормальных векторов заданных прямых:
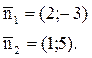
Теперь воспользуемся формулой (11.10)
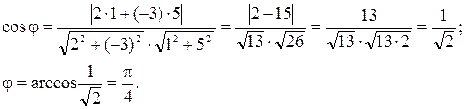
Дата: 2018-12-28, просмотров: 405.