Смешанное произведение векторов.

Определение. Смешанным произведением трех векторов 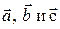 называется число, равное векторному произведению  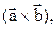умноженному на вектор 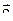, т.е. .

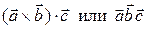Свойства смешанного произведения:

1. если

а) все три вектора компланарны;

б) любые два вектора коллинеарны.

2.

3. Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е.

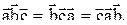
4. При перестановке двух соседних множителей смешанное произведение меняет свой знак на обратный, т.е.

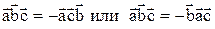
Модуль смешанного произведения трех векторов равен объему V параллелепипеда, построенного на этих векторах, как на ребрах:

V_парал.= 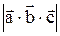                                                                                 (7.1)

Если векторы 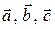 заданы своими координатами

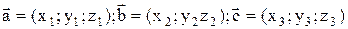, то смешанное произведение определяется формулой:

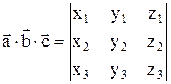                                                      (7.2)

Пример 1. Даны три вектора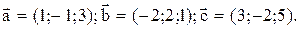

Найти объем параллелепипеда, построенного на этих векторах.

Решение:

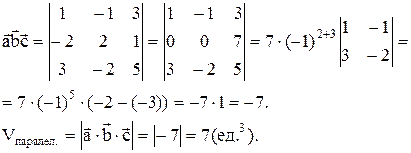
Пример 2. Выяснить, компланарны ли векторы

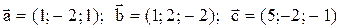
Решение. По 1 свойству смешанного произведения, если три вектора компланарны, то их смешанное произведение равно нулю.

Проверим это для наших векторов.

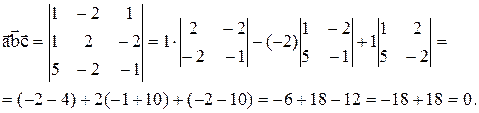
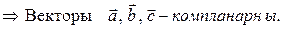
Лекция 7. Линии и их уравнения. Преобразование координат на плоскости. Полярная система координат.

Линии в полярной системе координат.

Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую OX, называемую полярной осью.

Пусть М-произвольная точка плоскости.

Длина отрезка ОМ=r, т.е. расстояние от

точки М до полюса О называется

полярным радиусом точки М, а угол

j=ÐxOM, отсчитываемый от полярной оси к отрезку ОМ против движения часовой стрелки - полярным углом.

Полярный радиус r и полярный угол j и составляют полярные координаты точки М: М(r, j).

Пример 1. Построить точки по их полярным координатам: А(5,0); В(3, p/2).

O

O                           r

Для самостоятельного решения. Построить точки по их полярным координатам М(2, p/4), C(1, p).

Переход от полярных координат к прямоугольным и обратно.

Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат OXY, а полярная ось является положительной полуосью OX.

Тогда для произвольной точки М имеем

ОА=x, AM=y, OM=r, ÐxOM=j.

Считая угол j острым, из прямоугольного

треугольника АОМ находим OA=OM×cosj

AM=OM×sinj или

.                                                                 (13.1)

Так выражаются прямоугольные координаты точки М через ее полярные координаты.

С другой стороны, из этого же прямоугольного треугольника АОМ получаем

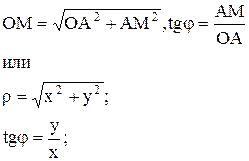                                                  (13.2)

                                                                              (13.3)

Так выражаются полярные координаты точки через ее прямоугольные координаты. В формулах (13.2), (13.3) предполагается, что полярный радиус r всегда положителен, хотя можно рассмотреть и отрицательные значения.

Пример 1. Найти полярные координаты точки А(2; -2).

Решение.

x=2; y=-1

Ответ: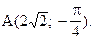

Пример 2. Записать уравнение окружности

x²+y²=25 в полярной системе координат.

Решение.

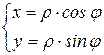
Подставим x и y в уравнение окружности:

Ответ: r=5.

Пример 3. Определить, какую линию представляет уравнение .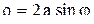

Решение. Переходя к прямоугольной системе координат, находим:

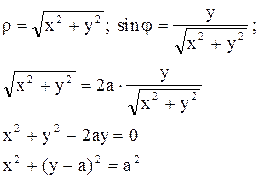
Это уравнение представляет окружность радиуса a, проходящую через полюс O и касающуюся полярной оси OX.