Скалярное и векторное произведение векторов. Применение.
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.
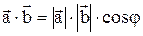 , (6.1)
, (6.1)
где 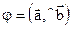
Углом между векторами называется угол между их направлениями
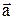

Свойства скалярного произведения.
1. 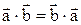 (переместительный закон).
(переместительный закон).
2. 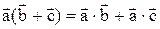 (распределительный закон).
(распределительный закон).
3. 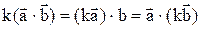 (сочетательный закон).
(сочетательный закон).
4. 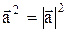
5. 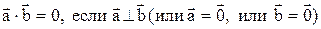
6. 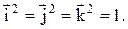
Если два ненулевых вектора заданы своими координатами 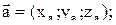
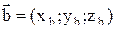 , то скалярное произведение этих двух векторов равно сумме произведений соответствующих координат:
, то скалярное произведение этих двух векторов равно сумме произведений соответствующих координат:
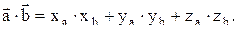 (6.2)
(6.2)
Тогда из (10.1) и (10.2) следует, что
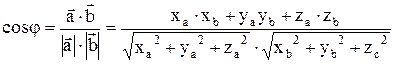 (6.3)
(6.3)
При умножении вектора на число получается коллинеарный вектор.
Пусть 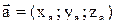 , тогда
, тогда 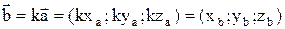
Признаком коллинеарности  двух векторов является пропорциональность их координат:
двух векторов является пропорциональность их координат:
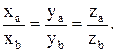 (6.4)
(6.4)
Признак ортогональности двух векторов 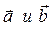 можно получить из (6.3)
можно получить из (6.3)
Если 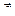 ^
^ 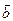 , то j =p/2, cosj=0
, то j =p/2, cosj=0
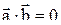 , т.е. (6.5)
, т.е. (6.5)
xa×xb+ ya×yb+ za×zb=0. (6.5*)
Пример. Найти скалярное произведение векторов 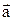 =(3; 5; 1) и
=(3; 5; 1) и 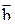 =(-1; 5; 2).
=(-1; 5; 2).
Решение. Используя формулу (10.2), получим
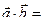 3(-1)+5×5+1×2=-3+25+2=24.
3(-1)+5×5+1×2=-3+25+2=24.
Пример. Найти угол между векторами 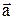 =(0; -1; +2) и
=(0; -1; +2) и 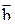 =(1; -2; 3).
=(1; -2; 3).
Решение. Используя формулу (10.3), получаем
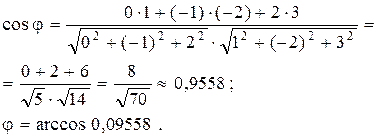
Определение. Векторным произведением вектора 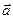 на вектор
на вектор 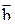 называется вектор
называется вектор 
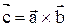 (обозначаемый иначе
(обозначаемый иначе 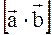 ), удовлетворяющий следующим условиям:
), удовлетворяющий следующим условиям:
1. 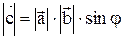 , где j-угол между векторами
, где j-угол между векторами 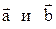 ;
;
2. 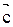 ^
^ 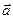 и
и 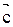 ^
^ 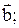
3. вектор 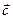 относительно векторов
относительно векторов 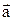 и
и 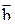 направлен так же, как координатная ось OZ относительно координатных осей OX и OY, т.е. векторы
направлен так же, как координатная ось OZ относительно координатных осей OX и OY, т.е. векторы 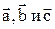 образуют правую тройку векторов (это значит, что если векторы
образуют правую тройку векторов (это значит, что если векторы 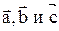 приведены к общему началу, то вектор
приведены к общему началу, то вектор 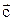 должен быть направлен так, чтобы из его конца наблюдался кратчайший поворот первого вектора ко второму, причем этот поворот осуществлялся бы против хода часовой стрелки:
должен быть направлен так, чтобы из его конца наблюдался кратчайший поворот первого вектора ко второму, причем этот поворот осуществлялся бы против хода часовой стрелки:
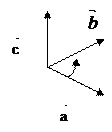
Основные свойства векторного умножения
1. Векторное произведение зависит от порядка сомножителей, т.е.
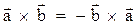 .
.
2. 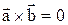 , если
, если 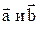 коллинеарны
коллинеарны 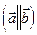 .
.
3. 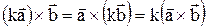 (сочетательный закон).
(сочетательный закон).
4. 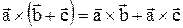 (распределительный закон).
(распределительный закон).
5. 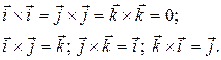
Модуль векторного произведения равен площади S параллелограмма, построенного на векторах 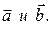
Если векторы 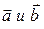 заданы своими координатами
заданы своими координатами 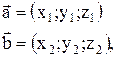
то векторное произведение вектора 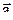 на вектор
на вектор 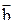 определяется формулой:
определяется формулой:
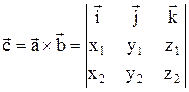 или, (6.6)
или, (6.6)
Если разложить определитель по элементам первой строки:
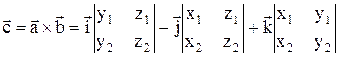 (6.6*)
(6.6*)
где i = (1;0;0), j = (0;1;0), k = (0;1; 0) – вектора Декартового базиса.

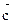
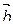
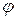
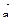
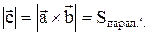 (6.7)
(6.7)
Площадь треугольника, построенного на векторах 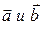 , равна
, равна
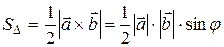 (6.8)
(6.8)
Пример 1. Упростить: 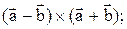
Решение:
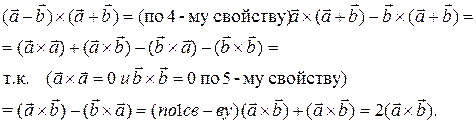
Пример 2. Вычислить 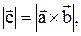 если известно, что
если известно, что 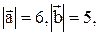 и векторы и векторы
и векторы и векторы 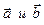 образуют угол j=p/3.
образуют угол j=p/3.
Решение:
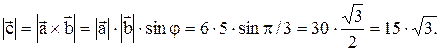
Пример 3. Векторы 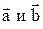 образуют угол j=p/6.
образуют угол j=p/6.
Зная, что 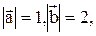 вычислить:
вычислить: 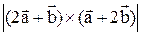 .
.
Решение:
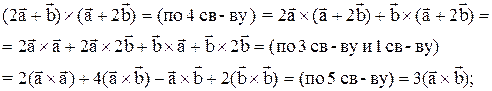
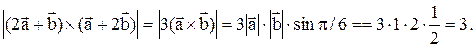
Пример 4. Даны векторы 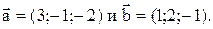
Найти координаты вектора 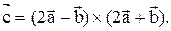
Решение: Найдем координаты векторов-сомножителей:
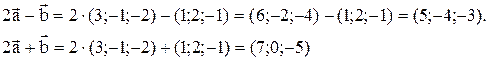
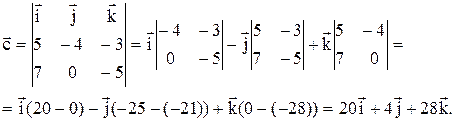
Таким образом, вектор 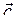 имеет следующие координаты:
имеет следующие координаты: 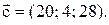
Дата: 2018-12-28, просмотров: 359.