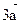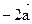Действия над матрицами. Вычисление обратной матрицы
Определение: Матрица - это множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов:
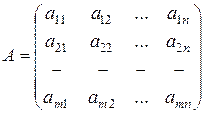 или A=(aij), где
или A=(aij), где 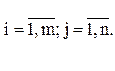
Для обозначения матрицы используют прописные латинские буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием номера строки и столбца, на пересечении которых стоит данный элемент. Запись «матрица B имеет размер mxn» означает, что речь идет о матрице, состоящей из m строк и n столбцов. Например, матрица 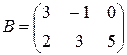 имеет размер 2x3. Далее, bij - обозначение элемента, стоящего на пересечении i-й строки и j-го столбца данной матрицы (в примере b23=5).
имеет размер 2x3. Далее, bij - обозначение элемента, стоящего на пересечении i-й строки и j-го столбца данной матрицы (в примере b23=5).
Матрица, у которой число строк совпадает с числом столбцов, называется квадратной. Элементы a11 , a22 ,…, ann квадратной матрицы A (размера nxn) образуют главную диагональ. Квадратная матрица, у которой отличные от нуля элементы могут стоять только на главной диагонали, называется диагональной. Диагональная матрица, у которой все элементы (главной диагонали!) равны 1, называется единичной. Наконец, квадратная матрица, у которой ниже (выше) главной диагонали находятся только нули, называется верхней (нижней) треугольной матрицей. Например, среди квадратных матриц размера 3x3
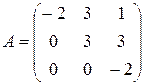 ,
, 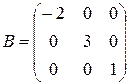 ,
, 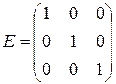 ,
, 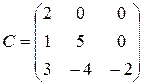
матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.
Замечание: нужно помнить, что матрица-это таблица, а определитель - это число.
Если m¹n, то матрица называется прямоугольной, если m=n, то матрица называется квадратной.
Определение. Две матрицы называются равными, если они имеют одинаковое число строк и одинаковое число столбцов, и их соответствующие элементы равны.
Определение. Если в матрице A типа m´n переставить строки со столбцами, получим матрицу типа n´m, которая будет называться транспонированной и обозначается AT.
Пример:
1) Если 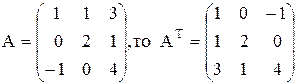 ;
;
2) Если 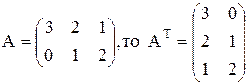 ;
;
3) Если 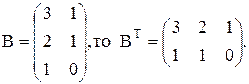
Действия над матрицами.
1. Сложение матриц.
Суммой двух матриц является матрица, элементы которой равны сумме соответствующих элементов этих матриц.
Замечание: складывать можно матрицы, имеющие одинаковое строение.
Пример1. Сложить матрицы А и В;
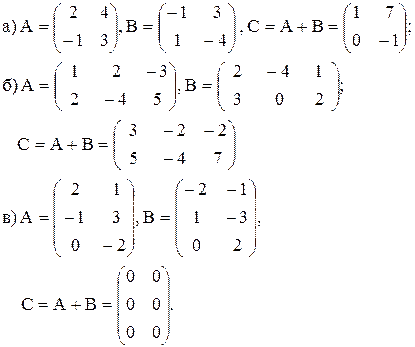
2. Умножение матрицы на число.
Произведением матрицы A=(aij) на число k называется такая матрица k×A, каждый элемент которой равен k×aij.
Пример:
а) умножить матрицу 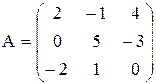 на число k=3:
на число k=3:
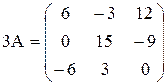 ;
;
б) найти матрицу, противоположную матрице 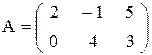 :
:
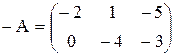 .
.
в) Найти 2 A- B, если 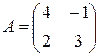 ,
, 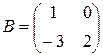 .
.
Решение. Сначала умножаем матрицу A на число «2», затем матрицу B на число «-1», и, наконец, находим сумму полученных матриц:
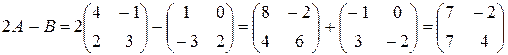
3. Умножение матриц:
а) умножение квадратных матриц
A×B=C.
Произведением двух матриц A и B является матрица С, каждый элемент которой Cij равен сумме произведений всех элементов i-й строки матрицы А на элементы j-го столбца матрицы B.
Пусть даны две квадратные матрицы
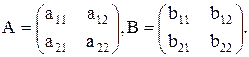
Тогда 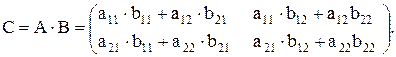 (8.1)
(8.1)
Пример. Найти произведение матриц А и В, если
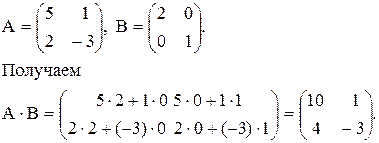 .
.
б) Правило нахождения матрицы-произведения распространяется на умножение прямоугольных матриц. Для умножения прямоугольных матриц справедливы следующие правила:
1) умножение матрицы А на матрицу В допустимо только тогда, когда число столбцов матрицы А равно числу строк матрицы В;
2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице и столько столбцов, сколько столбцов во второй матрице.
Произведение AB можно определить только для матриц A размера mxn и B размера nxp, при этом AB= C, матрица C имеет размер mxp, и ее элемент cij находится как скалярное произведение i-й строки матрицы A на j-й столбец матрицы B: 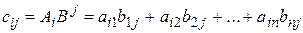 ( i=1,2,…, m; j=1,2,…, p). Фактически необходимо каждую строку матрицы A (стоящей слева) умножить скалярно на каждый столбец матрицы B (стоящей справа).
( i=1,2,…, m; j=1,2,…, p). Фактически необходимо каждую строку матрицы A (стоящей слева) умножить скалярно на каждый столбец матрицы B (стоящей справа).
Пример. Найти произведение матриц 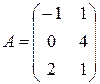 и
и 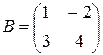 .
.
Решение. Размер матрицы A 3x2, матрицы В 2х2. Поэтому произведение АВ найти можно, произведение ВА – нет. Действуя по сформулированному выше правилу, получаем:
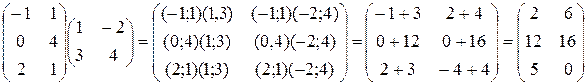
Пример. Найти произведение матриц А и В, если
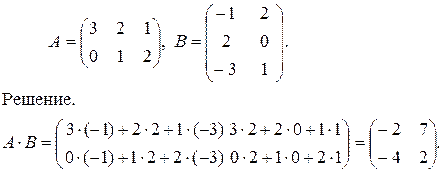
Пример. Найти произведение Е×А, где
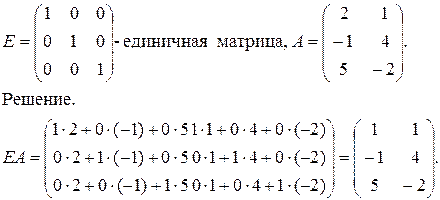
 Замечание. Произведение двух матриц не подчиняется переместительному закону, т.е. А×В¹В×А.
Замечание. Произведение двух матриц не подчиняется переместительному закону, т.е. А×В¹В×А.
Пример 3. Найти 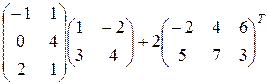 .
.
Решение. Воспользовавшись вычислениями, проведенными при решении примера, а также правилами умножения матрицы на число и сложения матриц, получим:
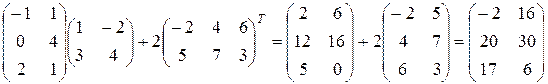 .
.
Вычисление обратной матрицы.
Определение: Квадратная матрица А называется вырожденной, если ее определитель равен нулю.
Определение: Если А - квадратная матрица, то обратной по отношению к А называется матрица, которая при умножении на А (как справа, так и слева), дает единичную матрицу.
Если А - исходная матрица, то обратная к ней обозначается А-1.
А-1×А=А× А-1 =Е, 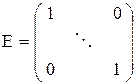 .
.
Определение: Пусть дана матрица А. Матрица, составленная из алгебраических дополнений элементов матрицы и затем транспонированная, называется взаимной к А и обозначается А*.
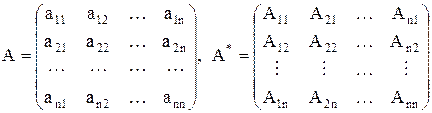 (8.2)
(8.2)
Обратная матрица А-1 получается путем деления каждого элемента взаимной матрицы на определитель системы D, т.е.
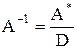 . (8.3)
. (8.3)
Любая невырожденная (D¹0) квадратная матрица имеет обратную матрицу. Причем А×А-1=Е. Таким образом, можно описать схему вычисления обратных матриц:
1) Найти определитель исходной матрицы (он не должен быть равен нулю).
2) Найти алгебраические дополнения всех элементов исходной матрицы и записать новую матрицу, состоящую из этих алгебраических дополнений.
3) Транспонировать матрицу, состоящую из алгебраических дополнений (т.е. записать взаимную матрицу).
4) Разделить полученную матрицу на определитель D.
Пример. Найти матрицу, обратную к 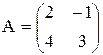 .
.
1) 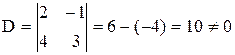 Þ матрица невырожденная, а значит, существует обратная.
Þ матрица невырожденная, а значит, существует обратная.
2) 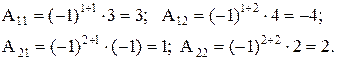
Получим новую матрицу
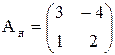 .
.
3) Транспонируем новую матрицу и получим взаимную к А матрицу: 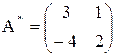 .
.
4) 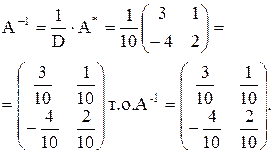
Проверим правильность полученного результата.
Если А-1 найдена верно, то должно выполняться условие: 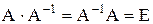 .
.
Проверим это
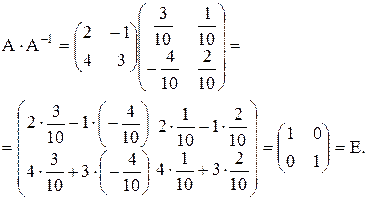
Полученный результат (А-1) правильный.
Нахождение обратных матриц применяется при решении линейных систем матричным методом.
Решение систем линейных уравнений матричным способом.
Пусть дана система уравнений
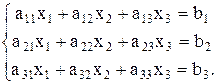 (9.1)
(9.1)
Рассмотрим матрицу, составленную из коэффициентов при неизвестных
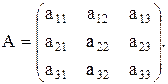
Свободные члены и неизвестные можно записать в виде матриц-столбцов:
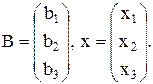
Тогда, используя правило умножения матриц, эту систему уравнений можно записать так:
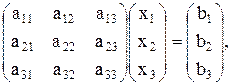 или А×X=B (9.2)
или А×X=B (9.2)
Равенство (5.2) называется матричным уравнением.
Такое уравнение решается по формуле:
X=A-1×B. (9.3)
Матричные уравнения решаются по схеме:
1) найти обратную матрицу А-1;
2) найти произведение обратной матрицы А-1 на матрицу-столбец свободных членов В, т.е. A-1×B;
3) записать ответ, пользуясь определением равных матриц.
Пример. Решить матричным способом систему уравнений.
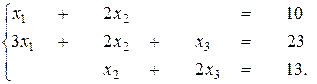
Составим матричное уравнение А×X=B, где
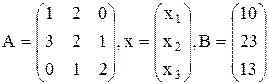 и решим его.
и решим его.
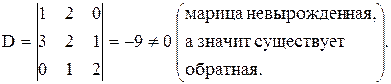
Найдем алгебраические дополнения элементов матрицы А:
А11= 3 А12=-6 А13= 3
А21=-4 А22= 2 А23=-1
А31= 2 А32=-1 А33=-4.
Составим матрицу из алгебраических дополнений
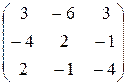 и транспонируем ее (тем самым получим взаимную матрицу).
и транспонируем ее (тем самым получим взаимную матрицу).
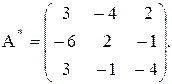
Запишем обратную матрицу:
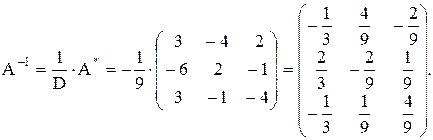
 Найдем решение системы:
Найдем решение системы:
X=A-1×B= 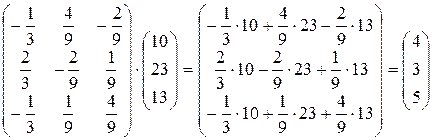 ;
;
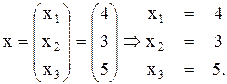
Результат можно проверить подстановкой в любое из уравнений системы, например, во второе:
3x1+2x2+x3=23;
3×4+2×3+5=23;
12+6+5=23;
23=23.
Второе уравнение обратилось в тождество после подстановки найденных значений неизвестных, а значит, получен правильный результат.
Ранг матрицы и его нахождение.
Определение. Рангом матрицы r называется наивысший порядок ее минора, отличного от нуля, при условии, что миноры более высокого порядка равны нулю.
Каждый элемент матрицы можно считать ее минором 1-го порядка.
Способы вычисления ранга матрицы.
1 способ. Вычислить всевозможные миноры n-го порядка и если хотя бы один из них окажется отличным от нуля, то ранг матрицы равен n. Если все миноры n-го порядка равны нулю, то вычислить миноры (n-1) порядка и так далее, пока не найдется первый минор, отличный от нуля.
Пример. Определить ранг матрицы
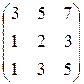 .
.
Вычислим минор 3-го порядка.
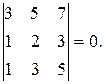
Будем вычислять всевозможные миноры 2-го порядка.
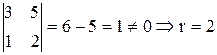
Ответ: ранг матрицы r равен 2.
2 способ основан на приведении матриц к ступенчатому виду.
Определение. Матрица называется ступенчатой, если каждая ее строка содержит хотя бы один элемент, отличный от нуля, который расположен правее (первого) отличного от нуля элемента предыдущей строки.
Пример.
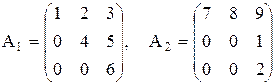
A1- ступенчатая
A2- не ступенчатая
2 способ состоит в том, что ранг матрицы равен количеству ненулевых строк ее ступенчатого вида.
Матрицу можно привести к ступенчатому виду с помощью элементарных преобразований ее строк:
1) перестановки строк;
2) умножения строк на одно и то же число;
3) прибавления к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число.
Замечание. Элементарные преобразования строк не меняют ранга матрицы; также не меняет ранга матрицы отбрасывание нулевых строк.
Пример.
Вычислить ранг матрицы: 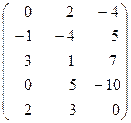
Решение.
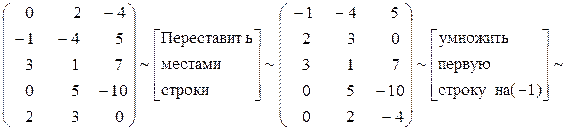


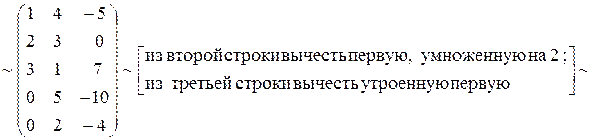

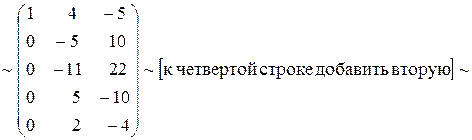
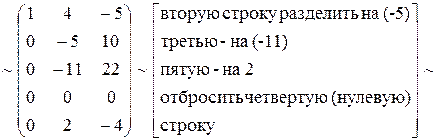
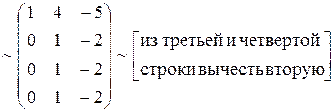 ~
~ 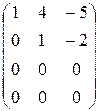 ~
~
~ 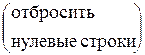 ~
~ 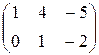 .
.
Полученная матрица имеет ступенчатый вид и у нее две строки  Þ r = 2.
Þ r = 2.
Лекция 4. Векторы, линейные операции над ними, способы задания.
Способы задания векторов и действия над ними.
Определение. Любой направленный отрезок принято называть вектором.
Определение. Отрезок называется направленным, если на нем задано начало и конец.
Вектор определяется числом и направлением. К числу векторных величин относятся сила, перемещение, скорость и т.д. Векторы обозначают либо одинарными латинскими символами: 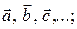 либо двумя заглавными латинскими символами, например
либо двумя заглавными латинскими символами, например 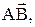 где А - начало направленного отрезка, а В - его конец. Геометрически вектор изображается направленным отрезком, соединяющим две точки пространства:
где А - начало направленного отрезка, а В - его конец. Геометрически вектор изображается направленным отрезком, соединяющим две точки пространства:

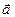 В
В 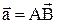 .
.
А
Чтобы задать вектор, достаточно указать его модуль и направление.
Также вектор 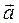 может быть задан координатами
может быть задан координатами 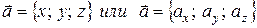 (4.1)
(4.1)
Определение. Модулем (длиной) вектора называется длина порождающего его отрезка.
Длина вектора обозначается таким образом: 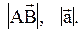
Пример. Записать векторы, изображенные на рисунке.
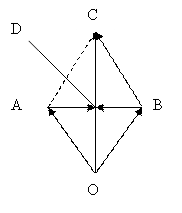 Так как первая буква в записи вектора должна обозначать начало вектора, то на рисунке изображены следующие векторы:
Так как первая буква в записи вектора должна обозначать начало вектора, то на рисунке изображены следующие векторы:
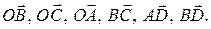
Определение. Вектор, модуль которого равен нулю, называется нулевым или нуль - вектором.
Очевидно, что 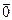 (нуль-вектор) - это точка.
(нуль-вектор) - это точка.
Определение. Если 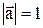 , то вектор
, то вектор 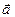 называется единичным.
называется единичным.
Координаты вектора 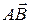 с началом в точке A(x1; y1; z1) и концом в точке
с началом в точке A(x1; y1; z1) и концом в точке
B(x2; y2; z2) определяются таким образом:
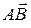 = (x2 - x1; y2 - y1; z2 - z1). (4.2)
= (x2 - x1; y2 - y1; z2 - z1). (4.2)
Определение. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
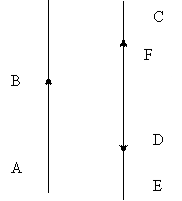
Коллинеарными являются векторы (см. рис.):
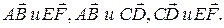
Причем, у первых двух коллинеарных векторов
направления совпадают. Такие векторы называ-
ются сонаправленными и пишут 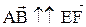 . Если направления у векторов противоположны, то их называют противоположно-направленными и пишут
. Если направления у векторов противоположны, то их называют противоположно-направленными и пишут 
Определение. Два коллинеарных вектора называют равными, если они сонаправлены и имеют равные длины.
Т. е. 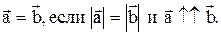
Также два вектора называются равными, если равны их соответствующие координаты, например, если 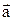 = (ax; ay; az) , а
= (ax; ay; az) , а 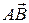 = (x2 - x1; y2 - y1; z2 - z1) , то
= (x2 - x1; y2 - y1; z2 - z1) , то
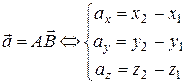
Вектор, полученный параллельным переносом вектора 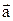 в пространстве, является равным вектору
в пространстве, является равным вектору 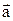 .
.
Определение. Векторы 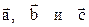 называются компланарными, если после приведения их к общему началу они лежат в одной плоскости.
называются компланарными, если после приведения их к общему началу они лежат в одной плоскости.
Линейные операции над векторами.
Определение 1. Суммой векторов 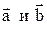 называется такой вектор
называется такой вектор 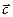 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 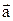 , а конец - с концом вектора
, а конец - с концом вектора 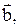 при условии, что начало вектора
при условии, что начало вектора 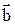 перенесено в конец вектора
перенесено в конец вектора 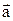 (правило треугольника).
(правило треугольника).
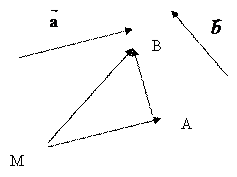 Пример 1. Таким образом, чтобы сложить два вектора
Пример 1. Таким образом, чтобы сложить два вектора 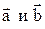 , нужно выбрать на плоскости произвольную точку М и отложить от нее вектор
, нужно выбрать на плоскости произвольную точку М и отложить от нее вектор 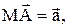 а затем от точки А отложить вектор
а затем от точки А отложить вектор 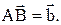 Тогда вектор
Тогда вектор 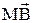 является суммой векторов
является суммой векторов 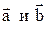 , т.е.
, т.е. 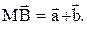
Определение 2. Суммой двух векторов 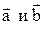
 является диагональ параллелограмма, построенного на этих векторах, исходящая из их общего начала (правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из их общего начала (правило параллелограмма).
Пример 2. Сложить векторы 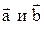 , пользуясь правилом параллелограмма.
, пользуясь правилом параллелограмма.

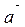
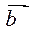
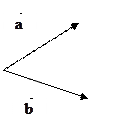
 Возьмем произвольную точку О на плоскости. Отложим от нее вектор
Возьмем произвольную точку О на плоскости. Отложим от нее вектор 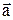 и вектор
и вектор 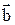 (приведем их к общему началу).
(приведем их к общему началу).

О
Построим на этих векторах параллелограмм.

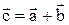
О
Тогда суммой векторов 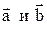 будет вектор
будет вектор 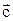 , являющийся диагональю параллелограмма и выходящий из общего начала векторов
, являющийся диагональю параллелограмма и выходящий из общего начала векторов 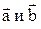 , т.е.
, т.е. 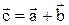 .
.
Отсюда сразу следует, что 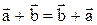 .
.
Сложение многих векторов производится при помощи последовательного применения правила треугольника.
Пример. Найти сумму векторов 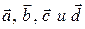 .
.

Возьмем произвольную точку М на плоскости и отложим от нее вектор 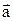 , затем от конца вектора
, затем от конца вектора 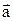 отложим вектор
отложим вектор 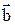 ; от конца вектора
; от конца вектора 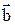 отложим вектор
отложим вектор 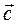 ; от конца вектора
; от конца вектора 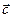 отложим вектор
отложим вектор 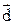 . Соединяя начало вектора
. Соединяя начало вектора 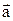 с концом вектора
с концом вектора 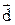 , получим результирующий вектор, являющийся суммой данных четырех векторов.
, получим результирующий вектор, являющийся суммой данных четырех векторов.

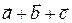

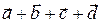
Определение. Сумма векторов 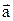 = (ax; ay; az) и
= (ax; ay; az) и 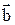 = (bx; b y; bz) – это вектор, координаты которого равны сумме соответствующих координат векторов слагаемых:
= (bx; b y; bz) – это вектор, координаты которого равны сумме соответствующих координат векторов слагаемых:
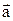 +
+ 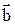 =
= 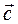 =>
=> 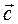 = (ax + bx; ay + by; az + bz ) . (4.3)
= (ax + bx; ay + by; az + bz ) . (4.3)
Определение. Два вектора называются противоположными, если их сумма равна нулевому вектору.
Вектор, противоположный вектору 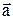 , обозначают
, обозначают 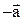 , т.е.
, т.е. 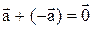 .
.
Таким образом, противоположные векторы имеют равные длины и противоположно направлены.
Определение. Разностью векторов 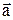 и
и 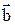 называют сумму векторов
называют сумму векторов 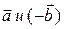 , т.е.
, т.е. 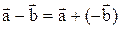 .
.
Если два вектора 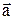 и
и 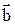 приведены к общему началу, то их разность
приведены к общему началу, то их разность 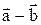 есть вектор, идущий из конца
есть вектор, идущий из конца 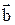 ("вычитаемого") к концу
("вычитаемого") к концу 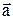 ("уменьшаемого").
("уменьшаемого").
Пример. Найти разность векторов 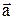 и
и 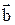

Возьмем произвольную точку М на плоскости и отложим от нее векторы 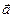 и
и 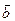
 Соединим концы векторов и направим этот отрезок из конца
Соединим концы векторов и направим этот отрезок из конца 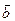 в конец
в конец 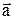 . Этот вектор и будет разностью векторов
. Этот вектор и будет разностью векторов 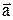 и
и 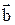 .
.
Определение. Произведением вектора 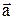 на число (скаляр) k называется вектор
на число (скаляр) k называется вектор 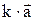 , который имеет длину, равную
, который имеет длину, равную 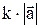 и коллинеарен
и коллинеарен 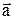 . При этом, если k>0, то векторы
. При этом, если k>0, то векторы 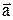 и
и 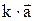 сонаправлены, если k<0, то они противоположно направлены.
сонаправлены, если k<0, то они противоположно направлены.
Произведение вектора 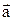 = (ax ; ay ; az) на число – это вектор, координаты которого равны координатам вектора
= (ax ; ay ; az) на число – это вектор, координаты которого равны координатам вектора 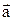 , умноженным на это число:
, умноженным на это число:
k∙ 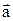 = k∙( ax ; ay ; az ) = ( k∙ ax ; k∙ ay ; k∙ az ). (4.4)
= k∙( ax ; ay ; az ) = ( k∙ ax ; k∙ ay ; k∙ az ). (4.4)
|













 k=-2
k=-2
|
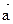
| ||||
 | ||||
|
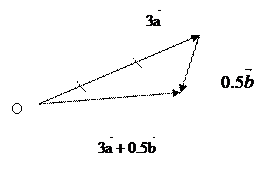
Пример. Даны векторы 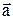 и
и 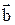 . Построить вектор
. Построить вектор 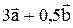 .
.
Возьмем произвольную точку О на плоскости. Отложим от нее 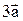 , а затем от конца полученного вектора отложим
, а затем от конца полученного вектора отложим 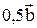 . Теперь соединим точку О с концом вектора
. Теперь соединим точку О с концом вектора 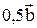 . Полученный вектор и будет результирующим.
. Полученный вектор и будет результирующим.

Единичный вектор того же направления, что и данный вектор. Длина и направляющие косинусы вектора.
Справедливо следующее утверждение:
Любой вектор 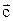 на плоскости может быть представлен единственным способом в виде линейной комбинации двух неколлинеарных векторов
на плоскости может быть представлен единственным способом в виде линейной комбинации двух неколлинеарных векторов 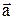 и
и 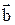 , т.е.
, т.е. 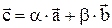 , где
, где 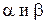 - числа.
- числа.
Говорят, что вектор 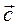 разложен в базисе
разложен в базисе 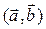 .
.
Определение. Базисом на плоскости называется пара неколлинеарных векторов, взятых в определенном порядке.
Определение. Числа 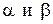 называются координатами вектора
называются координатами вектора 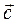 в базисе
в базисе 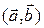 .
.
Пример. Разложить векторы 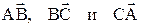 в базисе
в базисе 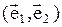 .
.

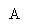
Решение: 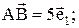
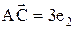 , а значит
, а значит 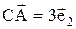 ,
, 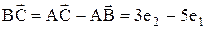
Таким образом, 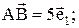
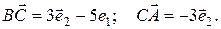
Также справедливо следующее утверждение: любой вектор в пространстве может быть выражен через тройку единичных векторов 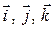 , направленных по осям координат, (которые называются ортами и образуют базис трехмерного пространства) при помощи линейных операций
, направленных по осям координат, (которые называются ортами и образуют базис трехмерного пространства) при помощи линейных операций
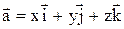 .
.
Определение. Проекцией вектора 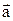 на ось Х называется число, равное величине соответствующего отрезка
на ось Х называется число, равное величине соответствующего отрезка 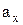 на оси Х.
на оси Х.
Проекция вектора 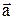 на ось Х обозначается:
на ось Х обозначается: 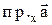 .
.
Проекция вектора 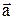 на ось Х выражается через его модуль и угол a к оси Х формулой:
на ось Х выражается через его модуль и угол a к оси Х формулой:
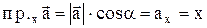 .
.
Аналогично
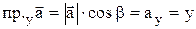 (5.1)
(5.1)
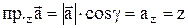
Определение. Проекции вектора на координатные оси называют его координатами.
Если вектор 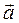 задан координатами
задан координатами 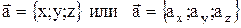 , то формула
, то формула 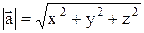 (5.2)
(5.2)
позволяет по координатам вектора определить его модуль.
Если даны две точки 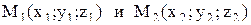 , являющиеся соответственно началом и концом вектора
, являющиеся соответственно началом и концом вектора 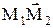 , то его координаты (x, y, z) определяются по формулам x= x2-x1, y= y2-y1, z= z2-z1.
, то его координаты (x, y, z) определяются по формулам x= x2-x1, y= y2-y1, z= z2-z1.
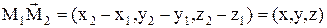 (5.3)
(5.3)
(Для случая, когда вектор задан на плоскости, третья координата будет отсутствовать).
Модуль вектора 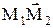 будет определяться по формуле:
будет определяться по формуле:

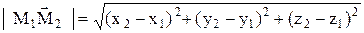 (5.4)
(5.4)
Пример. Найти длину вектора 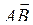 , если А(5; 2), В(8, -2).
, если А(5; 2), В(8, -2).
Решение:
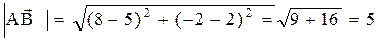
Ранее уже сообщалось, что если векторы заданы своими координатами, то:
1) при сложении двух и большего числа векторов их одноименные координаты складываются, т.е.
если 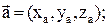
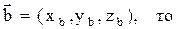
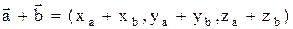 ;
;
2) при вычитании векторов их одноименные координаты вычитаются:

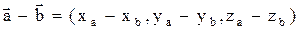 ;
;
3) при умножении вектора на число каждая координата вектора умножается на это число:
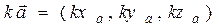 .
.
Пример. Даны точки А(2; 1; 0), В(1; 2; -1), С(-1; 1; 2).
Найти: 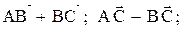
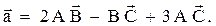
Решение. Найдем координаты используемых векторов: 
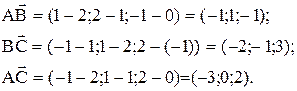
Тогда
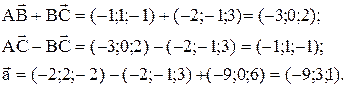
Определение. Если a, b, g - углы, которые составляет вектор 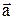 с координатными осями: то
с координатными осями: то 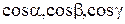 называются направляющими косинусами вектора
называются направляющими косинусами вектора 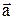 .
.
Вследствие формул (9.1) и (9.2)
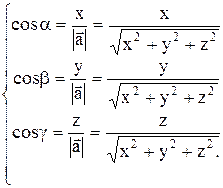 (5.5)
(5.5)
Отсюда следует, что 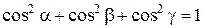 .
.
Деление отрезка в данном отношении.
Пусть отрезок АВ задан координатами своих концов А(xa , ya, za) и В(xb, yb, zb).
Точка М делит отрезок АВ в заданном отношении  (l - число). В этом случае координаты точки М определяются по формулам
(l - число). В этом случае координаты точки М определяются по формулам
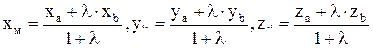 (5.6)
(5.6)
Пусть точка М делит отрезок АВ на две равные части, тогда 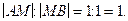 Подставив это значение в формулы (9.6), получим
Подставив это значение в формулы (9.6), получим
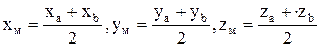 .
.
Пример. Точка С делит отрезок АВ в отношении 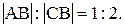
Найти координаты точки С, если А(6; 4; 2), В(-2; 1; 4).
Решение. Подставим 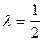 и координаты точек А и В в формулу (5.6) и находим:
и координаты точек А и В в формулу (5.6) и находим:
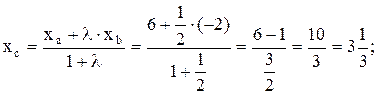
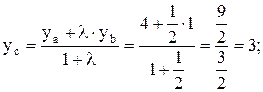
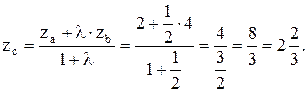
Таким образом, 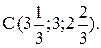
Дата: 2018-12-28, просмотров: 468.